土壤风蚀是风力与土壤表面相互作用下的综合自然地理过程，是干旱半干旱地区土壤退化的主要原因^［1-2］。中国的土壤风蚀灾害严重。风蚀量的计算是土壤风蚀研究中的核心问题^［3］。土壤风蚀预报方程是定量评价风蚀量动态变化、防治土壤风蚀以及进行水土保持生态效益评价的重要手段。输沙通量预报方程是为了准确预测风蚀量、指导土地的可持续利用发展起来的，主要通过大量观测资料的统计、分析与模拟而来^［4-5］。所有的输沙通量预报方程都包括基于特定环境的风洞测量或现场测量的经验校准系数，这些系数并不是固定的，会随着研究场地微地貌特点、风蚀可蚀性、风蚀力特性等因素而变化^［6］。然而这些方程的系数通常在理想化条件下通过率定得出，忽略了风蚀过程中一些影响因子的动态变化。很多经验系数是由风洞实验得来的，但风洞实验无法真正模拟自然界的环境，因此输沙通量预报方程往往在大田环境下需要进行修订。对河北省坝上地区康保县2017年和2018年两个地点的野外实测数据进行分析，与Bagnold方程、Kawamura 方程、Zingg方程、Lettau方程4个输沙通量预报方程进行比较，通过野外实测数据将4个方程重新率定得到新的经验系数，分析不同时间尺度下不同地点的经验系数及其与时间、风蚀可蚀性等因素的关系，提高方程的模拟能力。

两个实验地点位于河北省坝上地区康保县（41°25′—42°08′N、114°11′—114°56′E）。康保县位于河北省西北部^［7］，平均海拔1 450 m，地势东北高，西南低，年均气温1.2 ℃，无霜期114 d，年均降水量350 mm，年平均风速为2.99 m·s^-1，春季平均风速最大，风蚀事件多发，是京津沙源地，农田风蚀灾害尤为突出^［8-9］。本研究基于河北省康保县农田的两次典型风蚀事件，发生时间分别为2017年4月19日（地点1：41°55′37″N、114°27′28″E，海拔1 480 m）和2018年4月30日（地点2：42°07′54″N、114°48′22″E，海拔1 303 m）。地点1的农田在2016年10月底小麦收获后用一种铧犁（耕作深度为25 cm）翻耕，圆盘耙耙平。2018年3月下旬，在播种莜麦之前，地点2的农田由旋耕机（耕作深度20 cm）进行翻耕。实验场大致为西北—东南方向。地点1的上风向为天然草地，北面为小麦田，下风向为耕地。地点2的西、北、南迎风边缘为灌丛沙堆，下风向为耕地。为了避免灌丛沙堆影响迎风气流，在地块距离灌丛沙堆50 m处，用塑料网布制作的防尘屏障建造了一个20 m长的人造不可蚀边界（图1）。

绝大多数的输沙通量预报方程预报结果与真实的输沙通量有较大差距，这与方程的经验系数不断发生变化有关系。风蚀事件期间土壤性质在变化，方程的经验系数也应可变。方程的经验系数反映了土壤的可侵蚀性，与土壤表面砾石覆盖度、土壤含水率以及土壤结皮等各种参数有关^［10-11］。在研究区两个实验地点分别采取10 kg表层土壤样品（0~2 cm深），土样在实验室风干之后进行了土壤理化性质分析，采用Malvern Mastersizer 3000激光粒度仪确定粒度分布，用铬酸滴定法确定有机质含量，用烘箱干燥法计算土壤含水率等。表1列出了表层土壤（0~2 cm深）的理化性质，这两个地点的土壤类型为沙质壤土，土壤表面比较干燥，有机质含量较低。两个地点的土壤可蚀组分（<0.84 mm的干团聚体）分别为80.26%和78.28%。土壤干团聚体（<0.84 mm）一般被认为是比较容易受风力侵蚀的部分，Zachar^［12］提出当土壤可蚀组分（<0.84 mm的干团聚体）大于50%时可认为土壤具有高度可蚀性。这两个地点的有机质含量低，砂土含量高，土壤含水率低，使土壤干团聚体更容易破碎。这表明，两个地点都极容易发生风蚀事件，且随着风蚀事件的进行，表层土壤的理化性质也会不断发生变化。

两次风蚀事件中使用河北师范大学自主设计研发的自动连续称重式集沙仪进行集沙（图1），自动连续称重式集沙仪（cyclone type continuous-weigh sand trap， CCST）具有测量精度高、能够高频连续集沙的优点^［13］。自动连续称重式集沙仪（CCST）的6组仪器沿主风向连续设置，仪器距实验场地的不可侵蚀边界的距离分别为20、40、70、100、130、160 m（图1）。CR6数据采集器（Campbell Scientific Inc.）记录了自动连续称重式集沙仪的1 min平均的风蚀物质量。地点1和地点2的自动连续称重式集沙仪的入口方向分别设置为270°和310°（0°为正北）。集沙口高度分别设为0.05、0.15、0.4 m。输沙通量使用以下公式^［14］计算：

式中：Q_z为进沙口高度为z时的输沙通量（g·cm^-2·min^-1）； z是进沙口距离地面的高度（m）；a和b是回归系数。两块试验田较为平坦，土表粗糙度较低，采用3个高度的集沙量就可以估算集沙仪的输沙通量^［15］。因此，0~40 cm每分钟的输沙通量可以用以下公式计算：

使用Fryrear等^［16］提出的方程拟合描述风沙流沿程变化规律，该方程描述风程长度与输沙率之间的关系式为：

式中：f_x为风程长度为x时的输沙率；f_max为饱和输沙通量；b被定义为关键地块长度，是f（x）等于0.63（1-e^-1≈0.63）f_max时的风程长度^［17］。使用R软件中的最小二乘非线性回归 （Gauss-Newton iterative algorithm）拟合计算f_max和b。

将Met One风速仪布设在距离不可侵蚀边界40 m的位置，与同侧的自动连续称重式集沙仪（CCST）相距5 m（图1），用于测量高度1.2 m处的风向。距离不可侵蚀边界100 m的位置安装一台梯度风速仪，与自动连续称重式集沙仪（CCST）相距5 m，梯度风速仪9个风杯的高度分别为0.05、0.1、0.3、0.5、0.8、1.0、2.0、3.0、4.0 m（图1）。梯度风速仪的分辨率为0.1 m·s^-1，使用CR1000记录1 min的风速数据。使用最小二乘法来确定土壤表面空气动力学粗糙度Z₀，Z₀是评估输沙率的一个重要参数，空气动力学粗糙度越小，风沙输送的速度越快。然后将观测到的风速数据通过最小二乘法进行拟合，得到计算风速的公式：

式中：U_Z是高度为Z时的风速；A和B是回归系数。空气动力学粗糙度Z₀可由公式算出：

由此，摩阻风速可以通过“墙面定律”计算：

式中：U_Z是高度为Z时的风速；U_*是摩阻风速；k是von Karman常数 （0.4）。

计算出U_*后可以进一步计算起动摩阻风速U_*t^［18］：

式中：A是一个值为0.085的常数；ρ是空气密度；ρ_s 是表层空气密度；g是重力加速度（9.8 m·s^-2）；d是研究场地平均粒径。计算表明，地点1的起动摩阻风速为0.217 m·s^-1，地点2的起动摩阻风速为0.197 m·s^-1。

在风蚀研究领域，大多数输沙通量预报方程都是从空气动力学的角度出发，利用风速或摩阻风速来建立的^［19］。根据野外实验获得的实测数据选取了Bagnold方程、Kawamura 方程、Zingg方程、Lettau方程4个输沙通量预报方程来进行进一步的分析。

Bagnold^［20］率先将边界层理论和物理学方法运用到输沙通量预报方程中：

式中：q为输沙率（kg·m^-1·s^-1）；ρ是空气密度；g是重力加速度（9.8 m·s^-2）；d是研究场地平均粒径；D是粒径参数，值一般为0.24 mm或者0.25 mm；U_*是摩阻风速；C_B是针对天然沙粒的为1.8的经验常数，会随着表层沉积物的变化而变化。

Kawamura^［21］是第一个明确地将临界摩阻风速加入到方程中的人，他的方程也使用了物理参数：

式中：U_*t是临界摩阻风速；C_K是一个值为2.78的经验常数，它会随着表层沉积物的变化而变化。

Zingg方程与Bagnold方程十分相似^［22］：

式中：C_Z是一个值为0.83的经验常数，它也会随着环境的变化而变化。

Lettau方程进一步扩展了Kawamura方程的工作，因为该方程同样用临界摩阻风速去表达输沙率^［23］：

式中：C_L同样是一个随着表层沉积物变化而变化的值为6.7的经验常数。

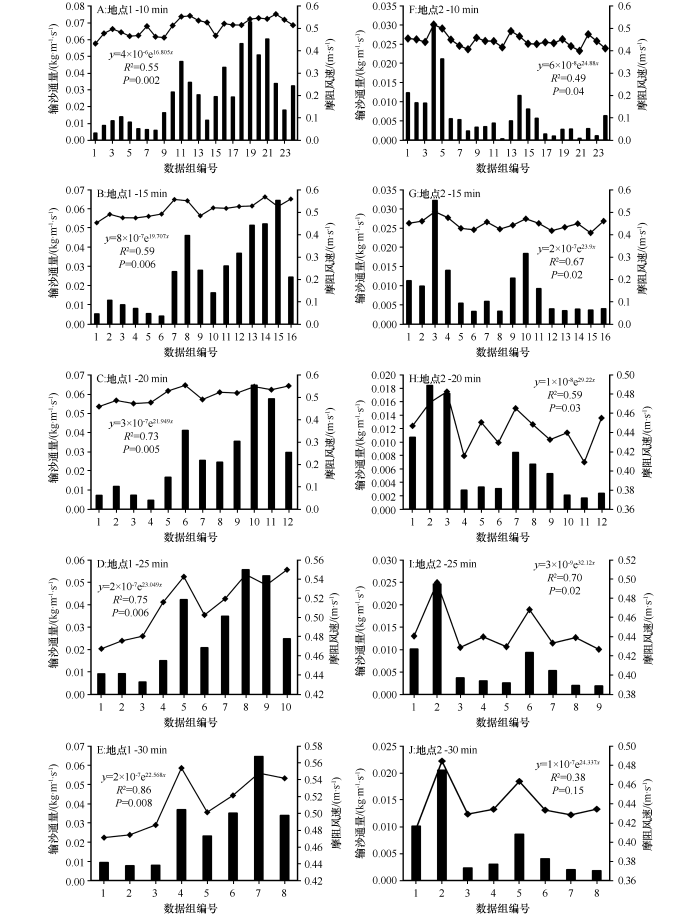
两次风蚀事件发生在不同时间、不同地点，风蚀事件一发生在2017年4月19日，风蚀事件二发生在2018年4月30日，本研究对两次风蚀事件都选取了4 h的风速和输沙通量数据进行分析，然后将4 h的数据分成10、15、20、25、30 min等5个时间尺度进行计算。风速是影响风蚀量的重要因素，把观测到的风速数据利用拟合得到的公式计算出摩阻风速。然后计算了两个地点的不同时间尺度的饱和输沙通量f_max，由于自动连续称重式集沙仪记录的数据单位为g·cm^-2·min^-1，为与输沙通量方程预测结果量纲一致，将实测输沙通量数据的单位转换为kg·m^-1·s^-1。将摩阻风速与输沙通量分别用指数函数和幂函数拟合后发现，指数函数拟合得到的相关系数均大于幂函数，输沙通量在风速较低时增加缓慢，在到达某一临界风速后迅速增加，说明输沙通量随摩阻风速的变化更遵循指数函数。从图2可以看出，除地点2的30 min时间尺度（R²=0.38， P>0.05），两个地点的输沙通量与摩阻风速具有较好的相关关系（P<0.05）。

得到摩阻风速与输沙通量的定量关系后，将4个方程在不同时间尺度上的预测值与实测值进行了拟合。通过比较R²和NSC（Nash-Sutcliffe Coefficient）来评定方程的模拟能力^［24］。NSC的计算公式为：

式中：O_i为实测值；P_i为预测值；O_m为所有实测值的平均值。NSC表示实测值与预测值对回归线y=x的符合程度，NSC≤0表示方程无模拟能力，0<NSC<0.6表示模拟能力较弱，NSC>0.6表示模拟能力较强，结果可接受，NSC=1表示模拟效果最好，预测值与实测值相等^［25］。比较方程的R²和NSC后发现，在地点1中，各方程的R²普遍较大，说明实测值与预测值之间相关性很好，在各时间尺度中只有Bagnold方程NSC值为正数，模拟能力稍好，其他3个方程均为负数，说明方程模拟能力很差，但Bagnold方程NSC值小于0.6，模拟能力较弱。地点2中，R²也普遍较好，说明实测值与预测值之间相关性很好，但只有Zingg方程NSC值为正数，其他3个方程均为负数，说明Zingg方程模拟能力要优于其他方程，但Zingg方程NSC值小于0.6，模拟能力也比较弱（表2）。R²和NSC表现出来差异的原因可能是方程系数或者起动摩阻风速不够好。

比较实测值与各方程预测的输沙通量后发现，预测值与实测值相差较大，这主要是因为本文采用的方程是基于理想的风洞实验环境下得出的，方程建立采用的风速、土质和土壤环境等因素与农田环境下进行的野外实验有很大区别。以往的研究发现，方程的经验系数是可变的，它与风蚀可蚀性、风蚀力特性等因素相关，采用原方程的经验系数得到的预测值与实测值相差较大，降低了方程的模拟能力。因此，我们有必要重新校正方程，获取适合试验点的方程经验系数。我们先将原方程的经验系数移除得到一组新的预测值，再将实测值与新的预测值进行线性拟合得到一个y=ax的方程，y为实测值，x为预测值。这个a值我们就可以认为是更适用于本研究两个地点方程的经验系数（表3）。而新的经验系数是随着时间变化的，在任一时间尺度内，地点1的新经验系数都大于地点2。

在以往的研究中，绝大多数输沙通量与风速的关系都表达为幂函数，这些关系是在沙源丰富、地面平坦、植被覆盖度小的沙漠地区得出的。本研究分别用指数函数和幂函数对输沙通量和摩阻风速拟合后发现，本次实验农田环境下输沙通量与摩阻风速的关系更符合指数函数，且实测的输沙通量与摩阻风速相关性明显。造成这种差异的原因主要是农田地区土壤性质与沙漠地区差异比较大，植被覆盖度高，受侵蚀后地表粗化严重^［26］。两个地点的土壤容易形成地表结皮，提高了地表的抗侵蚀能力，使得输沙通量在风速较低时增加缓慢，在到达某个临界风速后迅速增加。研究不同时间尺度的输沙通量和风速时发现，较小的时间尺度产生了较大的风速和输沙通量，较大的时间尺度产生了较小的风速和输沙通量，因为各时间尺度的风速和输沙通量都进行了平均化处理，风速在到达某个阈值时输沙率才会显著提高，而采用较大的时间尺度时减少了计算使用的数据量，一些超过阈值的关键风速可能被平均化处理而删除，降低了气流湍流的脉动性。因此，选用合适的时间尺度对计算输沙通量有重要影响，理论上讲时间尺度越小越好。

在没有调整经验系数的情况下，比较各个方程的预测值与实测值的R²和NSC值发现，R²普遍比较大，在地点1中，Bagnold方程预测的结果比其他3个方程稍好一些，在地点2中，Zingg方程预测的结果比其他3个方程稍好，但总体来说，不同时间尺度方程的NSC值都小于0.6，说明方程的模拟能力都比较差。在输沙通量方程中，经验系数、起动摩阻风速（U_*t）与颗粒平均粒径（d）是相互关联而又不确定的参数^［27］，而原始方程使用的各参数是基于理想的环境下得出的，不适合农田的实验环境，这大大降低了方程的预测能力。经验系数反映了土壤的可蚀性^［10］，土壤可蚀性取决于土壤的理化特性。在使用实测值重新计算经验系数之后发现，时间尺度变化后，方程的经验系数也在变化，也是平均处理之后较大时间尺度的风速与输沙通量的脉动性和间隔性变差造成的。由于一个地点只观测了一场风蚀事件，无法确定经验系数与时间尺度之间的定量关系，在未来还需要做更多的工作。而在对比两个地点的输沙通量预报方程的经验系数后发现，在任一时间尺度，地点1的4个方程的经验系数都要大于地点2的4个方程的经验系数，这也符合地点1任一时间尺度的输沙通量要大于地点2的输沙通量。调整经验系数使方程与实测数据相匹配，可以提高模型的模拟能力，对以后的野外工作有重要意义。

本研究使用河北省坝上地区康保县两个地点的实测数据，将输沙通量与摩阻风速进行拟合，对Bagnold方程、Kawamura方程、Zingg方程、Lettau方程4个输沙通量预报方程重新进行了校准，得到了新的方程经验系数。

在本次农田的野外实验环境下发现， 两个地点不同时间尺度输沙通量随摩阻风速的变化更符合指数函数关系。

在采用原方程经验系数情况下，将方程的预测值和实测值拟合后发现，在地点1中，Bagnold方程比其他方程稍好，在地点2中，Zingg方程比其他方程稍好，但总的来说，各方程的预测能力都比较差。

将各时间尺度的风速与输沙通量平均化处理会降低数据的脉动性与间隔性。在其他参数不变的情况下再重新计算经验系数后发现，经验系数随着时间是不断变化的，这主要与各时间尺度对风速与输沙通量进行平均化处理有关。

综上所述，在农田中输沙通量随摩阻风速的变化呈指数函数，方程的经验系数随着时间不断变化，采用合适的时间尺度重新计算经验系数能提高方程的性能，但如何确定经验系数与时间、土壤理化性质之间的定量关系还需要做更多的工作。