0 引言
中国的沙漠铁路通车里程很长,沙埋铁轨、风蚀路基和磨蚀设备等风沙灾害对沙漠铁路安全运行产生了极大威胁[1]。因此,大量防护措施被布设于风沙灾害严重路段以保障风沙区交通运行安全。风沙灾害防护体系防护效益评价成为国内外学者持续关注的热点问题。
在研究早期,沙漠铁路风沙灾害防护依赖于防护林等生物措施,相关研究也主要围绕生物防护措施展开,通过野外实测或风洞模拟获取风速分布,使用风速降低程度表征生物防护措施的防护效益[2-3]。但是,随着沙漠铁路向自然条件更加恶劣地区延伸,受气候干旱、土壤贫瘠和低温冻害等因素制约,生物防护措施布设受到极大限制,挡沙墙等机械防护措施逐渐成为主要防护措施。同时,由于机械防护措施几何参数、相似条件更易于测量、表达,风洞模拟成为防护效益评价的重要手段。国内外学者采用风洞模拟实验方法,测定机械防护措施速度场,划分流场功能区,量化了机械防护措施材料、高度、孔隙度等结构特征对于防护效益及阻沙率的影响[4-7]。随着现代测量技术的不断进步,国内外学者又将风洞模拟实验和粒子成像技术相结合,实现了沙粒运动轨迹的可视化,描述风沙两相流湍流场,分析沙粒碰撞的力学和能量过程,初步提出了机械防护措施周围沙粒的运动特性[8-10]。风洞模拟实验方法极大推动了我们对于机械防护措施防护机理的理解,但净风实验并未考虑风沙两相流的重要影响,而携沙风实验沙粒相似性受到广泛质疑,风洞模拟实验也存在明显的局限性。
计算流体动力学(Computational Fluid Dynamics,CFD)依托流体力学、数值方法和计算机科学,从计算方法出发,利用计算机快速计算能力得到流体控制方程的近似解。与野外实测和风洞模拟实验相比,CFD技术面向自然场景,采用1∶1建模方式,突破了流相和相似性等问题的制约[11],且实验过程更加便捷、经济。近年来,国内外学者使用雷诺平均、大涡模拟等方法,对挡沙墙、草方格等风沙灾害防护措施周围流动进行研究[12-16],使用CFD技术结合可视化手段,对各种防护措施周围流动机理与局部运动情况进行分析,基于模拟实验进行工程优化设计。CFD技术进一步推动了面向工程的流体力学尤其是多相流体力学的发展,已逐渐成为计算分析机械防护措施周围复杂风沙两相流运动的重要工具。
青藏铁路二期工程由青海格尔木至西藏拉萨,全长1 142 km。其中,轻度以上风蚀区长度约269 km,尤以错那湖沿岸风蚀最为强烈[17]。由于自然环境条件恶劣,生物防治措施在该区域难以施行,错那湖沿线沙害路段布设了大规模的工程治沙措施。然而,当前防护体系需要定期清理积沙,耗费大量人力物力,防护体系亟待综合评价和系统优化。鉴于此,本研究基于野外调查和CFD技术,使用欧拉双流体模型对错那湖段防护体系三维流场进行数值模拟,解析风沙两相流涡量、湍流强度和沙物质斯托克斯数,以期阐明错那湖段防护体系风沙两相流运动特性,为沙漠铁路风沙灾害防治提供理论依据与科技支撑。
1 研究区概况
2 研究方法
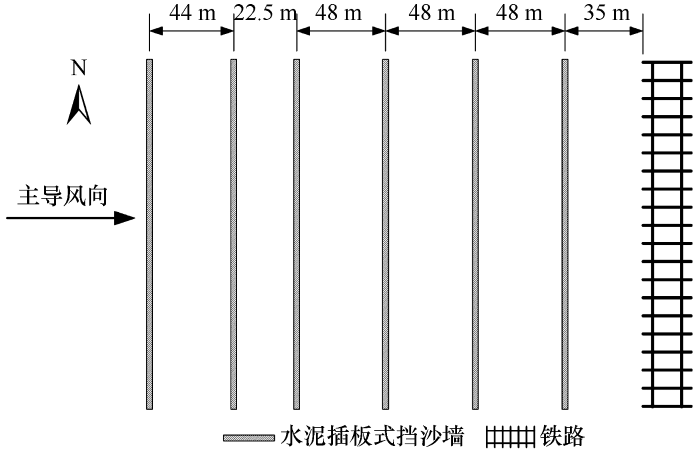
2017年8月,对青藏铁路错那湖段防护体系进行野外调查,调查内容包括:水泥插板式挡沙墙尺寸、铁路路基基础参数、沉积物情况以及错那湖段风信资料。错那湖段挡沙墙防护措施由结构相同的6道挡沙墙组成(图1)。为进一步简化模型,本文模拟了靠近铁路路基的两道挡沙墙周围的风沙两相流运动情况,对数值模拟参数设置及结果进行风洞验证后,使用Fluent欧拉双流体模型进行流场求解,基于风沙两相流相关理论,结合可视化分析,总结风沙两相流在挡沙墙周围的输运规律。
图1
图1
青藏铁路错那湖段挡沙墙防护措施
Fig.1
Control measures of wind-sand disaster in the Cuona section of QTR
2.1 控制方程及理论基础
在欧拉双流体模型中,将离散项视为流体求解,铁路沿线横向风速马赫数Ma≪1,流动满足不可压缩牛顿型流体运动N-S方程,对于任意相q,连续性方程及动量方程分别为:
式中:uqi是q相速度矢量在i方向上的分量;αq是q相的体积分数;ρq是q相的密度;p是所有相共享的压力;νq是q相的运动黏性系数;Sqi为源项。在实际求解中,气体动量方程中源项为0,沙物质动量方程中源项包含重力、压力梯度力及拖曳力。
在沙物质运动的过程中,颗粒的重力、压力梯度力以及拖曳力占主导作用,Syamlal-O’Brien模型用于描述沙相颗粒物质所受的拖曳力[22]。在两相流流动Syamlal-O’Brien模型中,相之间的曳力可以表示为:
式中:αg是气体体积分数,曳力函数CD采用Dalla Valle给出的形式:
在风沙两相流中,沙物质颗粒的雷诺数Res为[23]:
式中:ds为颗粒直径;Us、Ug分别为沙物质与气体速度;vg为气体运动黏性系数。
vr,s是与沙物质相关的末端速度:
式中:
N-S方程可通过速度压力耦合迭代求解速度场与压力场。本文流动的雷诺数较大,使用Realizable k-ε模型对N-S方程中雷诺应力项进行封闭。Realizable k-ε模型是在湍动能k单方程的基础上,引入湍流耗散率的双方程模型,同时在Standard k-ε模型的基础上改进了湍流模型常数Cμ,改进后的模型在流动分离和复杂二次流动预测中有很好的表现[24]。对于欧拉双流体模型,q相的湍动能k和湍流耗散率ε的输运方程及雷诺应力计算公式为:
式中:μq是q相的分子黏度;μqt为湍流黏度;Gk是由于平均速度梯度引起的湍动能;σκ、σε分别为湍动能和湍动耗散率对应的普朗特数。在Realizable k-ε模型中常数取值为:C1ε=1.44,C2=1.9,σκ=1.0,σε=1.2。
对不可压缩牛顿流体动量方程求旋度,得到涡量动力学方程:
对于有势力场,方程最后一项为0,涡量动力学方程可以写作:
公式左边为涡量沿流体质点轨迹的增长率,右边最后一项为涡量分子的黏性扩散,右边第一项为涡量生成项,sij是质点的变形率张量。使用涡量动力学方程,可以解释流场内涡量的生成与耗散,从理论上分析挡沙墙发挥防护作用的原理。
2.2 几何模型与网格划分
使用无网格模拟预实验,结合相关参数分析,挡沙墙后速度旋度具有在水平方向不可忽略的分量,进一步证实了进行三维数值模拟的必要性。由无网格模拟预实验得知流场在8 s之后趋于稳定,本文选取10 s后流场进行数据分析。
数值模拟实验的地物模型按照实地测量的尺寸建模,完全满足几何相似性,其中单个挡沙墙高2 m,宽1.8 m,平均孔隙度30.64%;路基高度4.85 m,长度21 m。通过无网格模拟确定了合理的计算域,调整后的三维计算域长184 m、宽5.4 m、高25 m。使用Ansys meshing模块进行非结构化网格划分,目标体尺寸2 m,网格体积增长率1.1,在靠近边界区域使用局部网格加密技术,进一步保证数值模拟的准确性。沙障插板孔隙、插板表面、立柱及路基表面尺寸分别为目标体尺寸的2.5%、15%、25%、25%,由于本文并未对边界层流动进行研究,受限于计算机性能,为增加沙障周围网格数量、提升沙障周围网格质量,未绘制近壁区域边界层网格。划分非结构化网格943万,平均网格质量0.85,平均扭曲度0.194,在Fluent中合并为238万多面体网格以减少计算资源加快模拟进程。
2.3 参数设置与计算求解
根据实际工况进行边界条件设置:近地表及接触挡沙墙、路基表面设置为具有粗糙高度的无滑移边界,壁面使用标准壁面函数;计算域上壁面、左右壁面设置为光滑对称边界,目的在于控制计算域大小,在实际环境中这些壁面并不存在;出口设置为压力出口,压力梯度
错那湖段平均海拔4 500 m,为准确模拟高原地区低压的气动力环境,根据ISO-2533-1975计算空气基础参数。在数值模拟求解中使用了代数多重网格法(AMG)加速收敛,迭代残差下降0.001视为收敛。使用Patch Conforming方法生成网格,在Fluent中使用Phase Coupled SIMPLE进行速度压力迭代。具体参数设置如表1所示。
表1 数值模拟具体参数设置
Table 1
| 参数 | 数值 | 参数 | 数值 |
|---|---|---|---|
| 地表、挡沙墙表面粗糙度/m | 0.05 | 空气密度/(kg·m-3) | 0. 752 |
| 路基表面粗糙度/m | 0.08 | 空气黏度/(Pa·s) | 1.6347×10-5 |
| 湍流强度 | 0.24 | 气压/Pa | 56 600 |
| 湍流耗散率 | 0.5 | 沙粒密度/(kg·m-3) | 2650 |
| 温度/K | 256.95 | 平均粒径/m | 1×10-4 |
| 重力加速度/(m·s-2) | 9.79 | 沙相比例/% | 0.02 |
Fluent中基于边界条件设置,对不同网格内物理量进行离散,代入连续性方程及动量方程,获得特征矩阵进行迭代求解。假设流体满足三维雷诺平均(RANS)方程,并存在于4 500 m标准大气环境之中;在计算域内地面为非滑移边界,流体以不可压缩的稳定入流速度的方式进入。使用Realizable k-ε模型对动量方程中雷诺应力项进行封闭,通过N-S方程结合速度压力耦合算法求解速度场与压力场。
2.4 数值验证与数据处理
为进一步量化和简化结果,选取计算域内11个XY特征截面(图2)进行数据处理,分析不同特征截面的流场特征;综合流场分布特征,选择Z=-1.975 m截面进行流场特征分析。
图2
图2
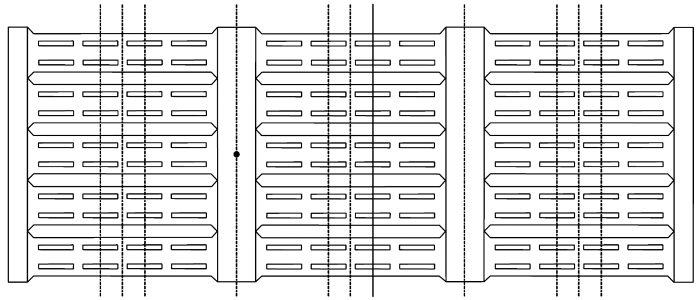
特征截面YZ平面示意图(挡沙墙模型高度2 m,宽度3×1.8 m,坐标原点位于从左往右第四个截面中部(h=1 m),实线位置为Z=-1.975 m XY截面位置)
Fig.2
YZ characteristic section (The sand-blocking fence height 2 m width 1.8 m model consist of three fences, the origin is located in the middle of the fourth cross section from left to right, the solid line is Z=-1.975 m XY section)
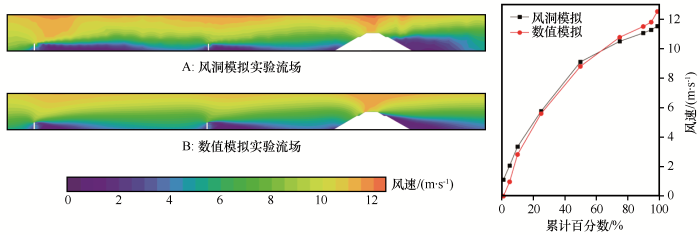
为验证数值模拟的参数设置与网格划分,将数值模拟结果与风洞模拟实验结果对比。风洞模拟实验在北京林业大学风沙物理实验室完成,风洞全长24.5 m,试验段长12 m,试验段横截面积0.6 m×0.6 m,风速脉动和湍流强度分别小于1%和0.8%。根据研究区大风季节风速分布情况和青藏铁路沿线沙物质起动风速[15,18],将轴心风速设定为9 m·s-1。以1∶50的模型实物进行模拟,使用三维移测系统和KIMO热线风速仪观测风速,风洞中风速测点以气流复杂结构为排列原则,分布在挡沙墙前30 cm至路基后50 cm范围内,取每个风速观测点30 s风速平均值为该测点时均风速,对点时均风速进行克里金插值获得流场。
由图3可知,风洞模拟与数值模拟流场整体运动规律相似,由于风洞模拟近壁面速度使用插值得到,第一道沙障后低速区相较数值模拟更长,路基后低速区范围更广。对流场内100×1300个克里金插值点进行统计,由于边界层风洞测量设备存在 ±3%的误差,数值模拟实验速度范围更广,测量的分辨率导致了气流结构在挡沙墙周围出现明显差异,数值模拟流场能更清楚地看到挡沙墙后速度变化情况。由于实验设备的限制,在风洞模拟实验中也无法获得速度矢量数据,无法对其涡量及气动力特性进行深入研究。借助可视化工具与统计手段,数值模拟能直观准确地定量分析风沙两相流中速度矢量以及涡量情况。
图3
风沙两相流在流经挡沙墙时会由无旋流动变为有旋流动,涡的作用会导致流体能量的损失,并使沙相沉积物的拖曳力发生变化获得二次赋能。使用气相物质的涡量来说明流场中涡量的分布情况,计算公式如下:
湍流强度是湍流中脉动均方根与平均风速的比值,能表征流场中阵风强度的大小,在三维笛卡尔坐标系中计算公式如下:
式中:I表示湍流强度;u′、v′、w′分别是速度在X、Y、Z方向的脉动。
涡旋结构会造成颗粒物浓度的选择性聚积,原因是颗粒的惯性阻碍了它们随流线的运动,这种现象也被称为局部富集效应。基于Kolmogorov时间尺度的斯托克斯数St是沙物质响应时间
式中:Ug为气相物质速度;
防风效能是平均风速比来流风速减小数值的百分比,是体现防护措施防护效益的一项重要指标,本文将风速降低60%的区域称为遮蔽效应区。防风效能的计算公式如下:
式中:Ux,z为距离挡沙墙x、高度Z处的平均风速;U0,z为试验高度Z处的初始风速,本文初始风速为入口速度15 m·s-1;Ex,z为距离挡沙墙x、高度Z处的防风效能。文中将速度进行归一化处理,归一化速度U/U∞是当地流速与来流速度的比值,归一化速度小于0.4时,防风效能大于60%。
3 结果与分析
3.1 流场时空分布特性
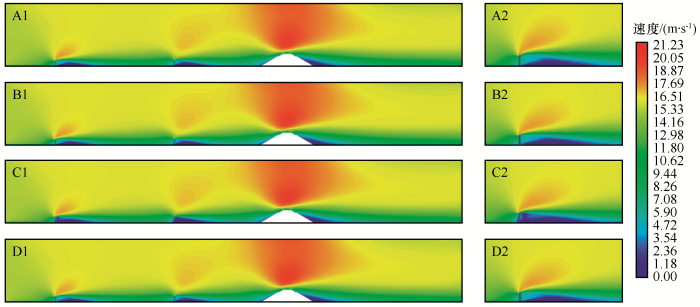
对比不同XY特征截面流场,挡沙墙立柱及其附近截面能量耗散更大,低速区明显大于挡沙墙中部截面,流动中具有不可忽略的水平速度分量,进一步论证了使用三维数值模拟才能准确模拟挡沙墙周围风沙两相流运动(图4)。在不同XY特征截面上,流场不尽相同,但整体运动规律相似。气流在第一道挡沙墙前2.5 H范围内遇阻减速;经过挡沙墙时发生转捩,能量在此处发生大量耗散;在挡沙墙及路基后发生边界层分离;在挡沙墙后1.5 H范围产生狭缝加速效应,挡沙墙后1.5 H~12 H范围速度降低明显。第一道挡沙墙前后速度降低更显著、狭缝加速区更长,第二道挡沙墙后低速区范围相较第一道更广。
图4
图4
计算域XY特征平面流场图(A. Z=0 m平面气相物质流场图,B. Z=-0.9 m平面气相物质流场图,C. Z=-1.975 m平面气相物质流场图,D.计算域气相物质平均流场图)
Fig.4
Flow field of XY characteristic section (A.Air flow filed of Z=0 m plane, B. Air flow filed of Z=-0.9 m plane, C. Air flow filed of Z=-1.975 m plane, D.averaged air flow filed of computational domain)
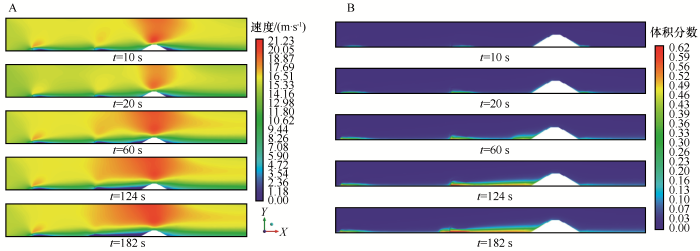
结合数据统计,在挡沙墙与路基之间2 m高度范围内,气流与沙物质速度平均值分别为3.17、3.00 m·s-1,气流与沙物质速度小于9 m·s-1的面积分别为69.82%、73.90%,沙物质在运动中减速更明显。对计算域非定常时变流场图进行分析,计算域内最大流速出现在路基上部,最小流速出现在沙障及路基后部;没有沙物质堆积时,挡沙墙后遮蔽效应区面积为65.34%,当前防护措施能发挥较好的防护作用(图5A)。随着时间的推移,沙物质在挡沙墙后不断沉积,路基及铁轨上逐渐出现沙物质,危及列车行车安全。
图5
图5
计算域XY特征平面时变流场(A)和时变沙物质体积分数(B)
Fig.5
XY characteristic section of time-varying flow field (A) and time-varying sand volume fraction (B)
防护效益与遮蔽效应区面积与沙物质堆积体积密切相关,随着沙物质堆积高度不断增加,起始沉积位置不断前移,防护效益不断减弱,124 s后铁路路基开始有部分积沙。沙物质最大体积分数可达0.62,最大堆积密度1 668.18 kg·m-3。沙物质沉降初期,两道挡沙墙后沙物质堆积高度基本一致,由于第二道挡沙墙后速度低速区范围更广,随着时间推移,第二道挡沙墙后沙物质堆积高度逐渐高于第一道挡沙墙。182 s时第二道挡沙墙后沙物质堆积高度为第一道挡沙墙的3.96倍,如果沙物质继续堆积,有掩埋防护措施的风险(图5B)。在实际应用中,为使防护体系持续发挥良好防护效益,防护体系需要定期清理积沙,消耗大量人力物力。
3.2 气相物质运动特性
气流穿过挡沙墙时,速度方向发生大幅变化,速度旋量的产生使能量大量耗散,穿过挡沙墙产生的速度旋量造成了流场变化,狭缝加速后的涡旋使沙物质更容易沉积。根据速度矢量及涡量分布情况,将流场划分为如图6所示7个功能区。气流在Ⅱ区遇阻减速,在挡沙墙上部抬升、加速,流场速度在Ⅲ区达到最大值,由于挡沙墙的存在,风沙两相流在穿过Ⅶ区时产生涡旋,在Ⅴ区、Ⅵ区旋流进一步发展,能量不断损耗,流场在Ⅵ区达到速度最小值、防风效能最大值,速度场在Ⅳ区逐渐恢复,耗散减速区、涡旋沉降区内防风效能在46%以上。
图6
图6
计算域流场功能区划分 (Ⅰ.初始速度区,Ⅱ.遇阻减速区,Ⅲ.加速抬升区,Ⅳ.速度恢复区,Ⅴ.耗散减速区,Ⅵ.涡旋沉降区,Ⅶ.狭缝加速区)
Fig.6
Velocity function division of flow field (Ⅰ.Initial velocity region,Ⅱ.Velocity reduction region,Ⅲ.Accelerate and uplift region,Ⅳ.Velocity recovery region,Ⅴ.Dissipate and decelerate region,Ⅵ.Sediment and vortex region,Ⅶ.Slit accelerate region)
两道挡沙墙后的流动具有相似性,由于两道沙障之间流动速度远小于入口处来流速度,第二道挡沙墙来流速度较小,经过第二次能量损耗,其遮蔽效应区大于第一道挡沙墙后遮蔽效应区。挡沙墙后1H~3H截线范围内涡量显著高于其他位置,气流在穿过挡沙墙时能量大量损耗,两道挡沙墙后速度旋量基本在0.5H~2.5H达到峰值,涡量在0.5H~3.5H激增。这样复杂的流动情况是无法借助传统风洞测量得到的,数值模拟便捷地提取大量网格点数据,能获得高分辨率的流动情况。
图7
图7
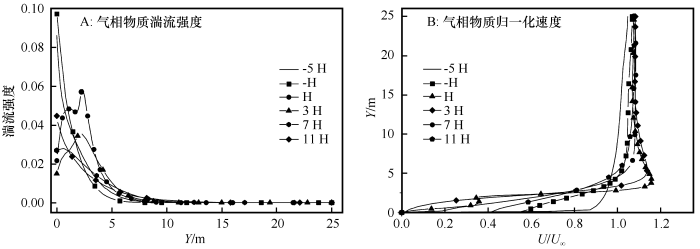
第一道挡沙墙前后不同Y截线气相物质特征值
Fig.7
Characteristic value on Y cutting line around the first fence
结合流场,对气相物质的涡动力学特性进行进一步分析,流场中涡量的生成项ω⋅∇U主要由挡沙墙贡献,旋流在穿过挡沙墙时产生,动能在涡旋中损失,质点变形率张量sij在挡沙墙附近达到最大值,由于涡量分子的黏性扩散作用,在挡沙墙后一段距离,涡量又逐渐减小,流速逐渐回复。能量在穿过挡沙墙时最大损耗量可达100%,铁路路基与挡沙墙间平均能量损耗55.31%。
3.3 沙物质输运特性
在气相旋流作用下,沙粒受力方向发生改变,逐渐运动到涡旋之间的剪切区域。受能量内耗、粒子碰撞的影响,当沙粒无法获得足够的离心力及压力梯度力时,沙物质逐渐聚集、沉降。在风沙两相流运动中,沙物质的运动还与颗粒振动、粒子间碰撞及粒子周围流动情况密不可分。
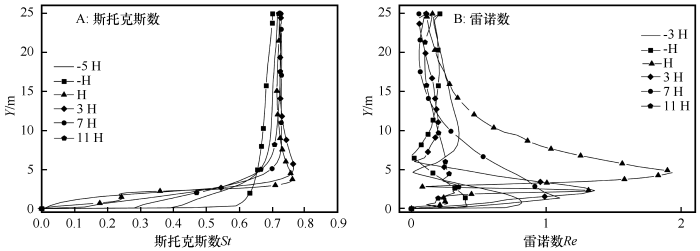
由于局部富集效应,沙物质在挡沙墙后1H~1.5H开始沉积,沙物质的沉积与基于Kolmogorov 时间尺度的斯托克斯数St密不可分。当0<St<1时,沙物质的局部富集效应随着St升高而升高。当粒子周围雷诺数大于1时周围流动变为湍流,湍流的出现可能使沙物质旋转、振动,进一步加大能量损耗,沙物质更易沉积。根据第一道挡沙墙周围气相物质特征值(图7)、沙物质无量纲常数(图8),风沙两相流速度旋量在穿过挡沙墙时产生,沙粒在狭缝加速区难以沉积,跟随气流运动到耗散减速区以及涡旋沉降区,在运动路径上,湍流强度大、流动复杂,由于空气密度远远小于沙粒密度,沙粒在此流动作用下逐渐减速,涡旋的进一步富集作用,沙物质在该区域大量沉积。
图8
图8
第一道挡沙墙前后不同Y截线上沙物质的无量纲常数
Fig.8
Dimensionless constant on Y cutting line around the first fence
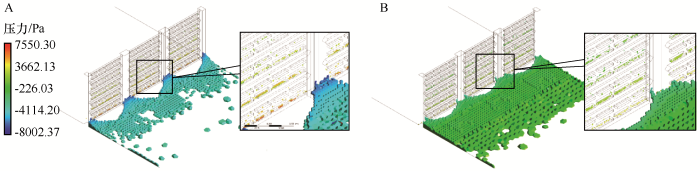
对计算域内沙物质体积分数进行统计分析,当沉积体积分数达到最大体积分数的90%时,在68.2%置信区间内气流与沙物质之间速度差值小于末端速度,将体积分数大于该数值的区域视为完全沉降区域。由沙物质60 s时在两道挡沙墙后堆积情况可知,两道挡沙墙前部基本没有沙物质沉积;第一道挡沙墙后堆积位置相较第二道挡沙墙距离挡沙墙更远,第一道挡沙墙后堆积沙物质表面的气压梯度力相较第二道挡沙墙后更高;第一道挡沙墙后堆积高度0.09 m,堆积体积0.97 m3,第二道挡沙墙后堆积高度0.15 m,堆积体积3.24 m3 (图9)。
图9
图9
第一道挡沙墙(A)及第二道挡沙墙(B)后沙物质堆积
Fig.9
Sand sediment volume of the first sand-blocking fence (A) and the second sand-blocking fence (B)
由于挡沙墙立柱后耗散大、速度低,比挡沙墙后其他位置更易积沙,虽然在其他位置沙物质从挡沙墙后1H~1.5H开始沉积,但是剪切和涡旋作用,沙物质在立柱后直接开始堆积,不均匀堆积使沙物质堆积位置更容易前移,防护措施的防护效益也随着沙物质堆积高度升高不断降低。
3.4 防护措施的优化
在以往研究中,国内外学者多用最大防护效益衡量防护体系的防护作用,然而在风沙灾害防治实践中,防护体系布设应追求长期防护效果而非最大防护效益。阻输结合和近阻远固的防护体系建设思想在前人研究中有所提及但并未付诸实践[7],以防护体系内风沙两相流动力特性研究为基础,设计了一种阻输结合的防护措施以提高防护体系的防护效益。
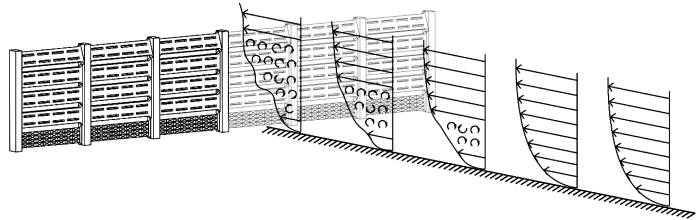
由涡动力学分析可知,防护措施风沙两相流的能量损耗主要由挡沙墙贡献,涡量生成量与挡沙墙结构密不可分,整个防护措施中低速区大小与防护措施间距离息息相关。从挡沙墙结构入手,使挡沙墙上部挡板适当倾斜,以增加气流能量在挡沙墙上部的耗散量;挡沙墙下部挡板使用PE网或复合大孔隙材料,让气流在挡沙墙下部能顺利通过,沙物质起始沉降位置后移,这种结构理论上可以有效提高防护效益。新型挡沙墙正置图如图10所示,将其气流运动方向调向可以得到反置的新型挡沙墙。
图10
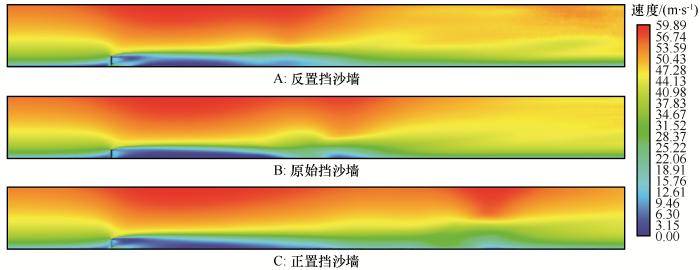
在极端大风天气下(风速32 m·s-1),对阻输结合的新型挡沙墙进行数值验证,改进后挡沙墙能使速度低速区显著后移,沙源物质一般在沙障后10~12 m开始沉积(图11)。正置挡沙墙防护效益远远高于反置挡沙墙及原始挡沙墙,相较原始挡沙墙,改进后的正置挡沙墙能使起始沉积位置后移1.47倍,将防护效益提高至原来的1.32倍以上,能有效提升防护效益、减少防护体系维护成本。在当前防护体系内建议布设4排及以上挡沙墙,两排沙障之间的间距控制在46~75 m。该阻输结合的挡沙墙有望成为提高防护效益、维持长效防护效益的新型防护措施,在风沙区铁路大量推广。
图11
图11
新型挡沙墙极端大风天气下的数值验证流场
Fig.11
Flow field of new sand-blocking fence under extreme gale weather
基于本文阻输结合的新型挡沙墙,可以进一步开发不同配置的上部挡板倾斜、下部多孔介质的阻输结合新型挡沙墙,采用不同方式的结构调整,使挡沙墙远地端能量耗散加大、近地端输运能力增强,进一步提高防护措施的防护效益,挡沙墙下部的多孔介质也可以考虑采用生态材料,探索绿色、环保的工程防护措施。同时,基于新型挡沙墙的评估结果,在今后的防护体系建设中可以使用近固远阻的防护体系建设思想,将新型挡沙墙布设在防护体系最前端,并适当增加防护措施与防护目标之间的距离,在提高防护效益的同时保证更长的防护时间,减少人力清理成本,设计复合型的防护体系取代当前铁路沿线单一的防护措施布设方式。
4 结论
青藏铁路错那湖段挡沙墙防风效果较好,但随沙物质不断堆积,遮蔽效应区面积不断增加,防护效益逐渐减弱。第二道挡沙墙后遮蔽效应区范围更广,其沙物质堆积体积也大于第一道挡沙墙。
计算域内流场可划分为初始速度区、遇阻减速区、集流加速区、速度恢复区、耗散减速区、涡旋沉降区和狭缝加速区7个功能区。集流加速区可以防止沙物质在铁轨上堆积,能量在耗散减速区、涡旋沉降区损失,沙物质在这些区域沉降,从而达到防护效果。
挡沙墙周围沙物质受涡旋作用局部富集,在离心力、拖曳力和压力梯度力作用下,逐渐运动到涡旋之间的剪切区域。沙物质在挡沙墙后1H~1.5H开始沉积。挡沙墙立柱后耗散大、速度低,比挡沙墙后其他位置更易积沙,沙物质在立柱后能直接沉积,使得沙物质堆积位置更容易前移。
上部倾斜、下部大孔隙阻输结合的新型挡沙墙能有效增大能量在远地端的耗散,使沙物质在近地端沉积位置后移,全面提高和长效维持防护效益,具有在风沙区铁路推广的潜力。
参考文献
Characteristics of the disastrous wind-sand environment along railways in the Gobi area of Xinjiang,China
[J].
Windbreaks:Their Influence and Value
[M].
Snow control on the high-ways
[J].
Wind protection by model fences in a simulated atmospheric boundary layer
[J].
A wind tunnel simulation of the mean velocity fields behind upright porous fences
[J].
Shelter effect efficacy of sand fences:a comparison of systems in a wind tunnel
[J].
Threshold velocity for wind erosion:the effects of porous fences
[J].
Evaluating the optimal porosity of fences for reducing wind erosion
[J].
Trajectories of saltating sand particles behind a porous fence
[J].
Computational fluid dynamics for urban physics:importance,scales,possibilities,limitations and ten tips and tricks towards accurate and reliable simulations
[J].
Computational fluid dynamic modeling of drifting particles at porous fences
[J].
Modelling and predicting wind velocity patterns for windbreak fence design
[J].
Numerical simulation of wind sand movement in straw checkerboard barriers
[J].
Design of a windbreak fence to reduce fugitive dust in open areas
[J].
Response of dune activity on the Tibetan Plateau to near future climate change
[J].
Particle cluster effects in the numerical simulation of a circulating fluidized bed
[M]// Avidan A A.
A new k-ϵ eddy viscosity model for high Reynolds number turbulent flows
[J].





 甘公网安备 62010202000688号
甘公网安备 62010202000688号