风是塑造地表形态的主要驱动力和地球表面重要的可再生资源，风力及其在时空尺度上的变异特征，是风沙地貌、土壤风蚀和沙漠化等领域研究的重要内容，也是风能资源开发利用重点关注的问题。风速概率分布是统计风速数据、进行风能资源评价的重要手段。其中，Weibull分布函数^［1］由于能够较好地反映实际风速频率分布而得到广泛应用^［2-11］。然而，相关研究主要证实了Weibull分布函数对描述风速概率分布的适用性，没有对该函数中的常数项可能存在的时空变化规律进行更深入的挖掘。陈练等^［12］利用中国557个气象站点长达40年的日均风速，统计得到日均风速的Weibull分布函数，并计算了平均风能密度和可利用风能时数，但没有考虑分布函数中参数的月际变化规律。有些学者虽然给出了Weibull分布函数中逐月、逐年不同的参数固定值^［13-14］，以及参数的月际变化规律^［15］，但未能建立能够反映月、年变化的统一概率分布函数，导致不同时间尺度风速分布之间缺乏应有的联系。此外，已有研究大多为日平均甚至月平均风速的概率分布，由于数据时间分辨率太低，导致在起沙风速统计、风能资源评价等应用中存在计算精度不足。

本文以地处内蒙古高原西部、风沙活动频发、风能资源丰富的阿拉善右旗为例，通过分析不同时间尺度整点风速的概率分布，尝试建立不同时间尺度的风速概率分布函数，以期为中国北方沙区风况数据的高效统计以及风能资源的快捷评价和预测提供有益参考。

采用的气象数据为阿拉善右旗气象站（39°13′N、101°41′E，海拔1 510 m）1960年1月1日至2020年12月31日整点风速数据。数据来源于中国气象数据网（http：//data.cma.cn/）。其中，1960—2015年数据用于统计不同时间尺度的风速累积频率分布，2016—2020年数据用于对所得到的风速累积概率分布函数进行检验。

不同时间尺度的平均风速，采用相应时段内的全部整点风速进行统计得到，包括1960—2015年逐年平均风速、1—12月逐月和1~365 d逐日多年平均风速。1960—2015年逐年、月、日风速频率分布，采用相应时段内的风速进行统计。将统计得到的频率数据，利用TableCurve 2D v5.01软件（SYSTAT Software Inc.）进行拟合分析，分别得到各时间尺度的风速概率分布函数，用均方根误差来检验风速概率分布函数对实际风速频率的拟合优度。

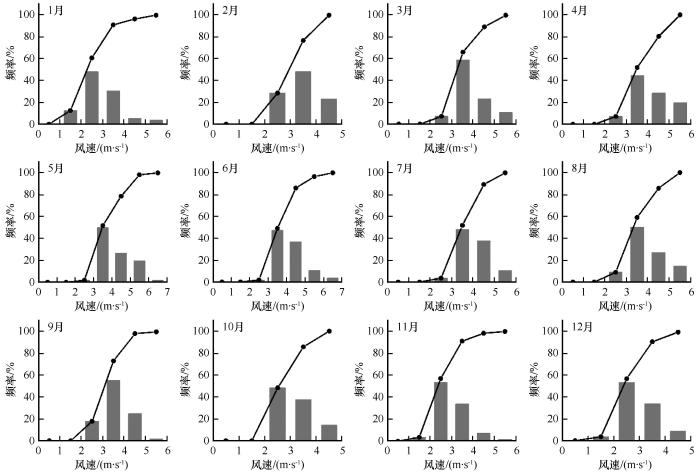
阿拉善右旗多年平均风速为3.63 m·s^-1，年均风速最大为5.00 m·s^-1（1972年），最小为2.86 m·s^-1（1992年）。总体而言，月平均风速以4—5月最大，在56年内只有5月和6月出现过平均风速大于6.0 m·s^-1的风速；11月至次年1月风速最小（表1）。2—6月，高风速频率逐渐增加，7月至次年1月高风速频率逐渐降低（图1）。

统计表明，逐日、逐月、逐年风速累积概率分布均符合WeibullCum函数分布：

式中：P_{（d，m，y）}为某日（1~365）或某月或某年风速小于U（m·s^-1）的累积概率（%）；A、B、C、D为分布函数中的常数项。

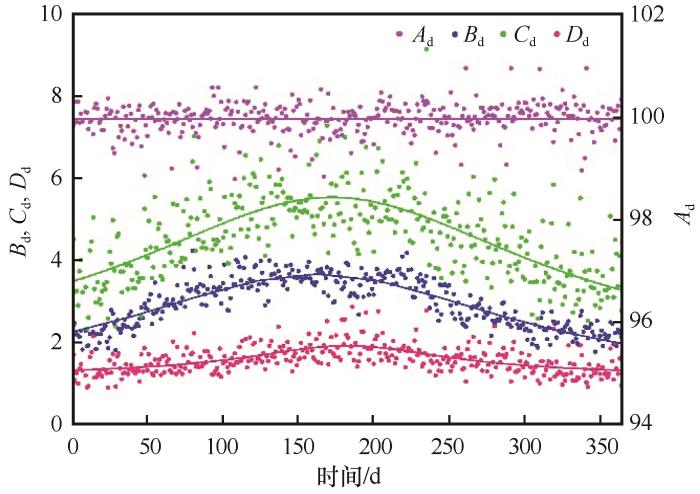
将逐日风速累积概率分布函数中的常数项A、B、C和D分别命名为A_d、B_d、C_d和D_d。其中，A_d在1~365 d中呈微小波动变化特征（标准差为0.31），不随日期发生趋势性变化，而是接近于一个定值99.94；B_d、C_d、D_d则不同，均随日期变化而表现为1—4月逐渐增大，5—7月处于峰值，8—12月逐渐减小至1月初的水平（图2）。进一步统计表明，B_d、C_d、D_d逐日变化趋势满足关系式（2）：

式中：x为日，介于1~365。B_d的函数关系式中，a=0.9285、b=2.7317、c=162.78、d=157.52；C_d的函数关系式中，a=1.5897、b=3.9262、c=172.51、d=165.49；D_d的函数关系式中，a=1.1872、b=0.7249、c=182.23、d=85.66。

将A_d=99.94代入（1）式，同时联立B_d、C_d、D_d的函数关系式，即可计算任意日期、任意风速范围内的风发生的概率。以4月10日为例（d=101），该日期10 m·s^-1以下风速发生的累积概率为P_d（U=10）=95.89%，11 m·s^-1以下风速发生的累积概率为P_d（U=11）=97.29%，则4月10日10~11 m·s^-1风速发生的概率为P_d（U=11）- P_d（U=10）=1.4%。17 m·s^-1以下风速发生的累积概率为P_d（U=17）=99.33%，则当日大风概率为1-P_d（U=17）=0.67%。

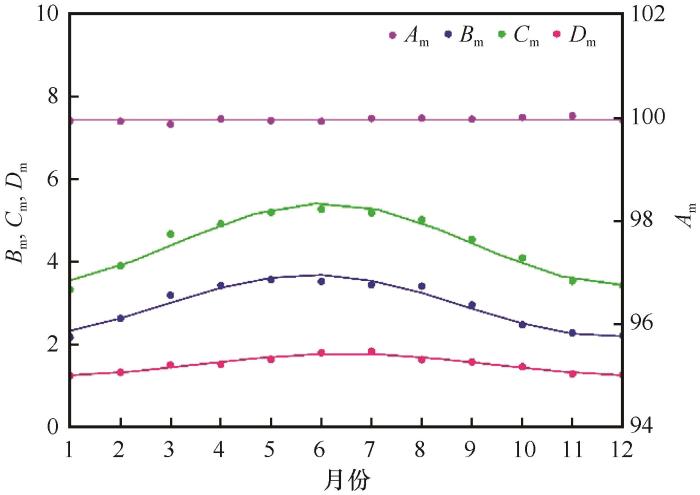
将逐月风速累积概率分布函数中的常数项A、B、C和D分别命名为A_m、B_m、C_m和D_m。其中，A_m为定值（A_m =99.94±0.09），不随月份而变化；B_m、C_m、D_m随月份不同而变化（图3），且满足相同形式的函数关系式（3）：

式中：x为月份。联立WeibullCum分布函数和（3）式，即可计算任意月份、任意风速范围内的风发生的概率。

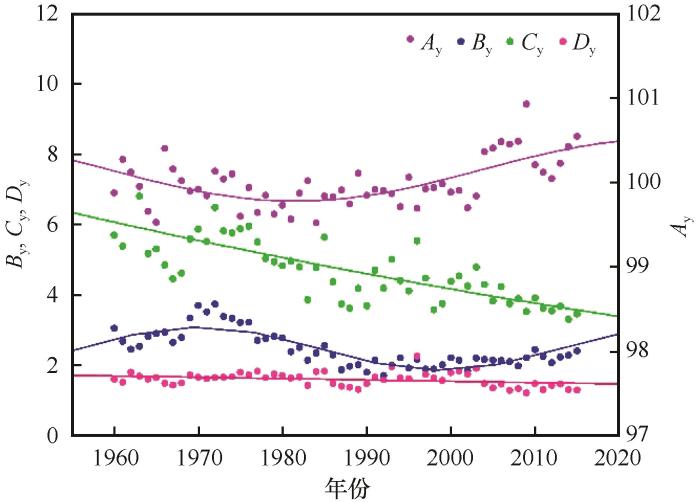
将逐年风速累积概率分布函数中的常数项A、B、C和D分别命名为A_y、B_y、C_y和D_y。结果表明，1960—2015年4个常数项均发生有规律的变化（图4）。其中，A_y和B_y的变化显示出一定的周期性，C_y和D_y 略具减小趋势。A_y、B_y、C_y、D_y分别与年份之间大致满足如下相关关系：

式中：x为年份。联立WeibullCum分布函数和（4）式，即可计算任意年份、任意风速范围内的风发生的概率。同时，利用（4）式，估算A_y和B_y的变化周期分别约为89年和57年。

大于临界起沙风速的风称为起沙风。临界起沙风速取决于地表植被覆盖和沙粒粒径、含水率等诸多因素^［16］，但在起沙风的统计中，一般并不考虑植被覆盖和沙面含水率等因素。陈渭南等^［17］在塔克拉玛干沙漠腹地的观测表明，该地区干燥、裸露沙丘沙的冲击起动风速约为6 m·s^-1（气象站观测的10 min平均风速，与整点风速记录相同）。在阿拉善右旗邻近的巴沙丹吉林沙漠，2 m高度的临界起沙风速被确定为5 m·s^-1［18］，同样接近于气象站观测的6 m·s^-1风速。本文采用的风速数据全部为气象站观测资料，因此将研究区临界起沙风速确定为6 m·s^-1，风速≥6 m·s^-1的风为起沙风。

利用逐日风速累积概率分布函数，计算逐日起沙风概率和可能时数。方法如下：

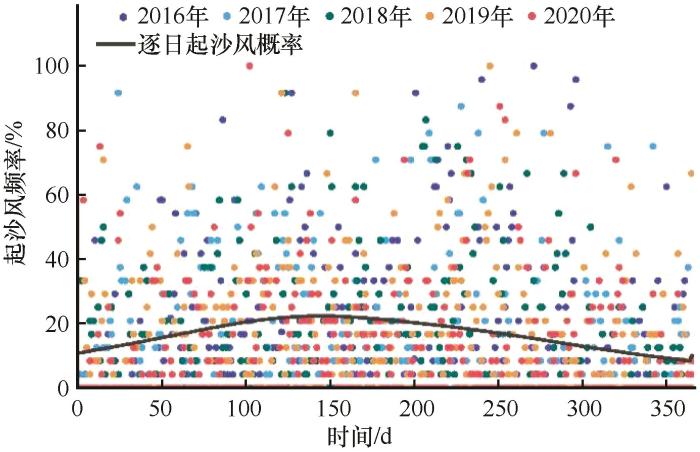
式中，P_d（U≥6）为某日起沙风概率；P_d（U=6）为当日风速等于6 m·s^-1的累积概率；T_d为当日起沙风可能时数（h）；T_d0为每日小时数（24 h）。计算表明，逐日起沙风发生概率和可能时数表现为第1~147天小幅度上升，第139~149天（5月18—28日）出现日起沙风概率和可能时数峰值（P_d（U≥6）= 22.3%，T_d（U≥6）=5.4 h）；147天以后日起沙风概率和可能时数逐渐减小至全年最低水平。逐日起沙风概率和可能时数最小值（P_d（U≥6）=8.4%， T_d（U≥6）=2.0 h）出现在第354~364天（12月19日至12月29日）。对比2016—2020年逐日实际起沙风频率与逐日风速概率分布函数计算得到的逐日起沙风概率，两者差异较大（图5），说明逐日风速分布具有很大的不确定性，利用概率分布函数进行日风速预测有局限性。

利用月风速累积概率分布函数，计算逐月起沙风概率和可能时数。方法如下：

式中：P_m（U≥6）为某月起沙风概率；P_m（U=6）为当月风速等于6 m·s^-1的累积概率；T_m为当月起沙风可能时数（h）；T_m0为每月小时数。逐月起沙风发生概率和可能时数表现为1—6月逐渐增大，6月出现全年起沙风概率的第一个峰值（P_m（U≥6）=23.1%，T_m=166.3 h）；7—12月起沙风概率和可能时数持续降低。起沙风概率最低月份是11月（P_m（U≥6）=11.4%，T_m=82.1 h）。对比2016—2020年逐月起沙风统计频率与采用逐月风速概率分布函数计算得到的逐月起沙风概率发现，前者符合后者的变化趋势（图6），均方根误差较小（2016—2020年均方根误差依次为0.027、0.026、0.026、0.027、0.030），说明逐月风速概率分布函数的预测能力较好。根据2016—2020年统计结果，逐月风速概率分布函数对5、6月的预测偏高；起沙风频率在8月份出现第二个峰值，但风速概率分布函数没有检测出该峰值，表明该分布函数对8月风速的预测能力欠佳。

利用年风速累积概率分布函数，计算阿拉善右旗逐年起沙风概率和可能时数，方法如下：

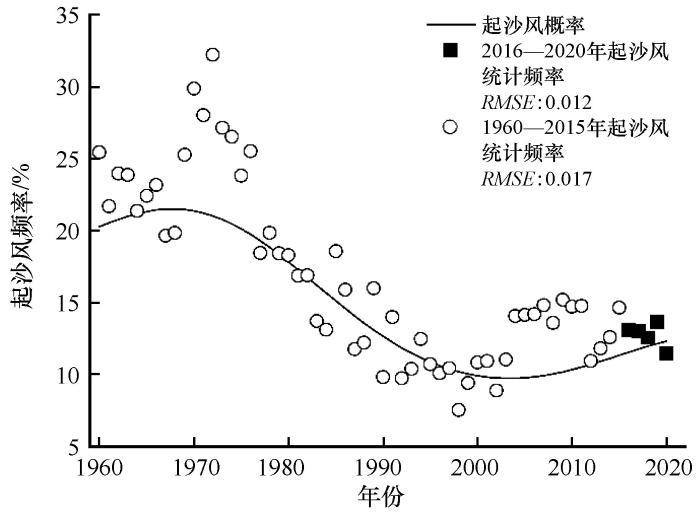
式中：P_{y（U ≥6）}为某年起沙风概率；P_y（U=6）为当年风速等于6 m·s^-1的累积概率；T_y为当年起沙风可能时数（h）；T_y0为每年小时数（8 760 h）。结果表明（图7），逐年起沙风发生概率和可能时数表现为1960—1968年逐渐增大，1968年出现多年起沙风概率和可能时数峰值（P_{y（U ≥6）}=21.5%，T_y=1883.4 h）；1969—2003年起沙风概率逐渐降低，2003—2015年起沙风概率逐渐增加，2003年是起沙风概率和可能时数最低年份（P_y（U≥6）=9.7%，T_y=849.7 h）。多年年平均起沙风概率为15.0%，可能时数为T_y=1316.4 h。

利用2016—2020年起沙风统计频率对上述逐年风速概率分布函数进行检验，发现该函数预测能力非常好，2016—2020年起沙风统计结果与函数预测结果之间的均方根误差（RMSE）仅为0.012（图7）。此外还可以看出，2016—2020年起沙风发生频率低于前56年平均水平。

阿拉善右旗风速在不同时间尺度上的累积概率都符合WeibullCum分布函数，表明该函数在描述风速累积概率分布时具有一定的普适性。函数中的4个常数项在逐日、逐月和逐年变化方面都表现出一定的规律性，这一特征使得该分布函数在引入时间变量后具备了预测能力。根据各时间尺度起沙风概率预测结果和实际发生频率统计结果，日起沙风概率预测效果较差，逐月起沙风概率预测能力明显提高，年尺度上的起沙风概率预测效果最好。

中国国土面积广阔，跨越不同的生物气候带，风况环境差异很大，虽然可以预期WeibullCum分布函数能够描述不同区域风速累积概率分布规律，但该函数中的4个常数项是否具有时空变化规律，尚需开展更深入和系统的研究。