0 引言
土壤颗粒分离、搬运和沉积发生与发展是风蚀研究的核心内容[3],对建立适用于中国北方地区的风蚀过程模型至关重要。土壤颗粒分离,即细颗粒脱离土壤母体进入空中,是其中的首要环节。在数十年风沙物理研究史中[4-5],颗粒分离时的临界动力条件和沙尘释放速率备受关注。气流直接吹蚀、跃移颗粒碰撞磨蚀、土壤团聚体在运动中破碎是3种基本分离方式[6]。对于松散床面,考虑气流拖曳力和重力作用,可从力矩平衡方程得到气流吹蚀时的临界起动风速表达式[7]。当粒径较小时,即使松散床面,颗粒间的内聚力也不可忽略。假设内聚力正比于粒径,仍可按同样方法推导出形式简单的临界起动风速公式[8]。跃移沙粒冲击松散沙土起尘速率正比于碰撞速度的2或3次方[9],对岩石磨蚀速率大约正比于入射颗粒的动能[10]。玻璃微珠对6种土壤的碰撞磨蚀实验表明[11],磨蚀速率与碰撞速度平方成正比。基于接触力学和强度理论的磨蚀模型[12-13]可用于探讨跃移颗粒对土壤的碰撞磨蚀过程,磨蚀变量代表了单位时间内的碰撞次数、土壤抗压强度和杨氏模量、入射沙粒动能和密度等综合效应,干燥致密土壤的磨蚀速率与之成正比[14]。不同于前两种分离方式,土壤团聚体在运动中的破碎过程和机制尚未完全被揭示。玻璃和陶瓷等脆性材料在受到冲击后所产生的碎片数量和尺寸满足特定的标度律。进而,可从理论上导出土壤团聚体破坏释尘的粒度分布[15]。虽然风沙运动中的颗粒空中相碰时有发生[16],但是与地面碰撞是土壤团聚体破坏的主要方式。
从大分子片段到细胞,从沙粒、石块到巨石,乃至地壳板块和超新星,均存在碰撞破碎现象。这种看似尺度上的巨大差异,但某种程度上内部破坏机制却存在一般性规律。对土壤团聚体跃移后与地面碰撞过程开展模拟实验,探讨土壤团聚体破碎时的临界破碎速度、粉尘释放量与粒径分布规律,揭示土壤团聚体与地面碰撞过程的破碎机制,对发展、完善土壤风蚀动力学模型具有重要意义。
1 材料与方法
1.1 团聚体制备
室内模拟实验需要制备球形团聚体以代替土壤颗粒开展碰撞破碎实验。由于制备过程中不可避免地会产生微裂纹及孔洞等微观上的缺陷,为减少团聚体形态差异对研究结果的影响,统一采用球形硅胶模具制作土壤球形团聚体。具体制备过程如下:①采集华北平原红黏土(38.31°N、114.37°E)、河套平原灌淤土(40.70°N、107.41°E)、黄土高原西部黄土(36.30°N、103.96°E)若干。土样预处理包括破碎、研磨、筛分,利用标准分样筛得到粒径小于63 μm土样备用。②将红黏土与灌淤土、黄土按照质量比1∶3混合形成其余两种混合土样。根据土壤质地分类标准,5种土样分别属于黏土、砂土、壤土、砂质黏土和壤质黏土。③筛分后的土样加水混合成半干状态,取适量泥块揉搓成团并置于粒径2、3、4、5、6 cm的球形硅胶模具之中。考虑实验的重复性和制作残次品,每种粒径的球形团聚体至少10个。④土壤团聚体在硅胶模具中静置24 h后基本成型。此时,团聚体含水率较高,由于自然晾干周期较长,利用烘箱在110 ℃下烘烤8 h取出备用。图1为烘干后不同粒径的黏土球形团聚体。尽管形状不同,土壤团聚体材料与此前磨蚀实验[14]的5种人工土壤基本一致。因此,没再单独开展压缩实验测定其抗压强度σ与杨氏模量E。
图1
1.2 碰撞实验
实验前,对5种土样制成5种粒径的若干球形团聚体依次编号,利用分析天平称量各团聚体的初始质量。实验时,球形团聚体置于实验场地中央,在某个高度以零初速度释放,经自由落体运动后,与水平刚性地面发生正碰并破碎。水平地面材料为陶瓷砖,其抗压强度远大于土壤团聚体,碰撞导致地面形变较小,故将水平地面近似看作刚体。团聚体碰撞速度如下式:
式中:h为团聚体释放高度;g为重力加速度,取9.81 m·s-2。
实验后,记录每个碎块的序号,并分别称量碎块质量mi。为方便后续分析,根据球体质量公式计算每块碎块的等效体积直径di :
式中:ρ为团聚体密度。
不同质量的碎片对应某一等效体积直径,最小分辨粒径为质量最小碎块的等效体积直径。实验中,最小分辨等效体积直径为2 mm。原因:一是小于此粒径的碎片已较难识别和称量;二是称量采用千分之一天平,其千分位为估读值,此粒径以下的碎块质量小于0.010 g,此时称量越小,误差越大。小于此粒径的碎块由团聚体原始质量与所有称量碎块的差值得到,这部分认为是粉尘释放量,主要包含微小碎片和细粉。
确定土壤团聚体临界破碎速度是本实验的难点。由于碰撞速度通过自由落体运动间接得到,为尽可能减少实验误差、提高精度,最终以10 cm高度为间隔从低到高依次释放,并观察团聚体表面的细微变化。当表面出现裂纹时,认为该高度为团聚体临界释放高度,碰撞速度为临界破碎速度。确定临界破碎速度后,继续增加释放高度,观察、统计不同释放高度下碎块的分布情况。
1.3 临界破碎速度和粒径分布
为分析土壤团聚体碰撞临界破碎速度v与密度ρ、粒径d、抗压强度σ、杨氏模量E参数之间的关系,选取ρ、d、E为3个独立的基本量,根据Π定理[17],得到两个无量纲参数Π1和Π2:
根据脆性材料碰撞破坏模型[13],无量纲数
式中:C和α由实验数据确定。方便起见,对
式中:d为粒径;P(d)为小于某一粒径d的累积概率;β为形状参数,也称为模数,与分布的分散性有关;η是比例参数,控制分布曲线的大小[20]。
本文选取等效体积直径d表征碎片尺寸分布的参数,对实验数据拟合,确定β、η参数值。为方便分析,对
2 结果与分析
2.1 碰撞破碎过程
球形土壤团聚体与刚性地面碰撞,按碎片分布分为无损状态、损伤状态和破碎状态[21]。观察团聚体碰撞过程,团聚体释放高度较低时,碰撞产生的作用力较小,土壤团聚体表面无明显裂痕以及细小碎片产生。此时认为团聚体处于无损状态。
图2
图2
不同数量贯穿裂纹产生的碎片分布
Fig.2
Distribution of fragments produced by different number of penetration cracks
图3
2.2 临界破碎速度
上述破碎过程分析中,仅讨论了有关裂纹形成和断裂产物的定性描述,不同破碎状态定量判定能更好分析碎片的形成与分布。在无损状态下,团聚体保持完整,无细小碎片产生,但损伤或者破碎状态下,团聚体破碎均会形成碎片和细微粉尘。临界破碎速度的确定能区分碰撞破碎状态,有利于分析碎片的粉尘释放和粒径分布。
以实验数据计算无量纲参数
图4
图4
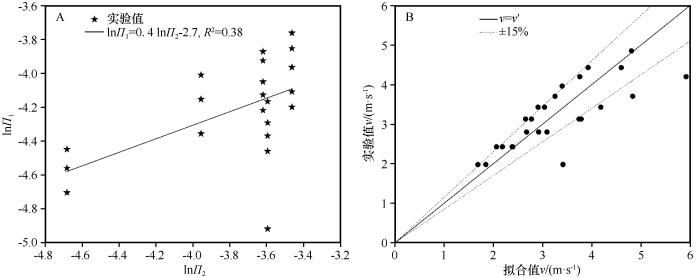
无量纲参数Π1与Π2线性拟合(A)及拟合值与实验值对比(B)
Fig.4
Linear fit of dimensionless parameter Π1 to Π2 (A) and comparison of fitted values and experimental values (B)
关系式中拟合优度R2=0.38,说明两个无量纲参数之间相关性较差,量纲分析时可能忽略了某些重要物理量。实验发现,粒径d对v有显著影响,考虑粒径影响对公式进一步修正。系数C和粒径的经验关系为:
式中:γ为待定参数。由实验数据拟合,v最终表达式为:
式中:γ=0.013 m1/2。
为进一步验证
经验公式准确性较低的原因:一是团聚体碰撞断裂过程中,材料的断裂表面能、泊松比、材料内部缺陷形状及分布、裂纹扩展、受力方式及受力状态等因素都会影响断裂破碎过程。在v、d、 ρ、σ、E参数关系的基础上进一步提高公式准确性,需要考虑碰撞过程相关的其他参数或物理量。二是团聚体破碎过程对内部缺陷敏感,很难准确测量其弹性模量和抗压强度,而文中不同粒径团聚体选用一个特定的弹性模量与抗压强度,也可能会导致理论值偏离实验值。
受实验手段限制,基于物理实验的团聚体破碎细观尺度的研究受到很大制约,本文并未进一步探索与讨论,进而给出准确性更高的经验公式。
2.3 粉尘释放量
碰撞破碎过程中粉尘释放量对起尘量有重要意义。以原始质量与所有碎块质量的差值为粉尘释放量,如图5所示,不同类型的土壤团聚体产生细微碎片和粉尘有所差别。
图5
图5
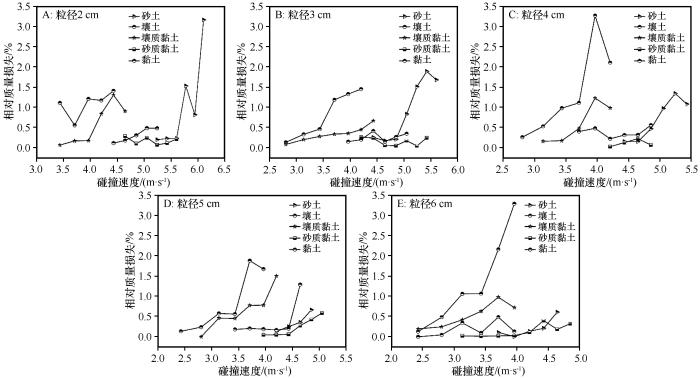
不同粒径球形团聚体不同碰撞速度时的相对质量损失
Fig.5
Relative mass loss of spheroids with different particle sizes at different impact velocities
随碰撞速度增大,各土壤团聚体同一粒径下相对质量损失总体呈上升趋势,团聚体粒径越大,临界破碎速度越小。不同粒径下,壤土相对质量损失随速度变化最为显著,平均相对质量损失为1.1%,同一碰撞速度下更容易产生细微粉尘,其余4种土壤的相对质量损失大部分小于1%。
砂土与壤土和黏土相比,在同一粒径下,其临界破碎速度更大,这意味着砂土团聚体相较于壤土和黏土更不容易破碎。砂土粒径在2、3 cm时粉尘释放量随碰撞速度快速增加(图5A、B),这是由于实验时碰撞速度过大,导致团聚体完全破碎而释放出更多的粉尘。黏土相对质量损失的变化介于壤土和砂土之间,平均相对质量损失小于0.5%。对混合土样而言,分析黏土和壤土以及砂质黏土和砂土的变化,二者的相对质量损失都有较大程度降低,这表明壤土和砂土中掺杂黏土能有效改善其力学特征,减少粉尘释放量。
2.4 碎片尺寸分布
表1 不同土壤类型团聚体碎片统计
Table 1
| 土壤 类型 | 粒径 /cm | 样本数 /个 | 释放高度 /cm | 各高度释放 次数 | 碎片数量 /个 | 土壤 类型 | 粒径 /cm | 样本数 /个 | 释放高度 /cm | 各高度释放 次数 | 碎片数量 /个 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 黏土 | 2 | 6 | 90~140 | 1 | 15 | 砂土 | 5 | 4 | 90~120 | 1 | 27 |
| 3 | 6 | 80~130 | 1 | 27 | 6 | 5 | 70~110 | 1 | 24 | ||
| 4 | 6 | 70~120 | 1 | 56 | 壤质黏土 | 2 | 6 | 60~110 | 1 | 31 | |
| 5 | 6 | 60~110 | 1 | 79 | 3 | 7 | 50~110 | 1 | 31 | ||
| 6 | 6 | 30~80 | 1 | 65 | 4 | 5 | 50~90 | 1 | 33 | ||
| 壤土 | 2 | 5 | 60~100 | 1 | 21 | 5 | 6 | 40~90 | 1 | 54 | |
| 3 | 6 | 40~90 | 1 | 33 | 6 | 6 | 40~90 | 1 | 46 | ||
| 4 | 6 | 40~90 | 1 | 40 | 砂质黏土 | 2 | 6 | 110~160 | 1 | 20 | |
| 5 | 6 | 30~80 | 1 | 37 | 3 | 7 | 90~150 | 1 | 38 | ||
| 6 | 6 | 30~80 | 1 | 52 | 4 | 4 | 90~120 | 1 | 29 | ||
| 砂土 | 2 | 6 | 140~220 | 1 | 27 | 5 | 7 | 70~130 | 1 | 53 | |
| 3 | 6 | 100~200 | 1 | 47 | 6 | 8 | 50~120 | 1 | 54 | ||
| 4 | 6 | 100~200 | 1 | 49 |
粒径2、3、4 cm砂土团聚体释放高度间隔为20 cm,其余团聚体释放高度间隔均为10 cm。
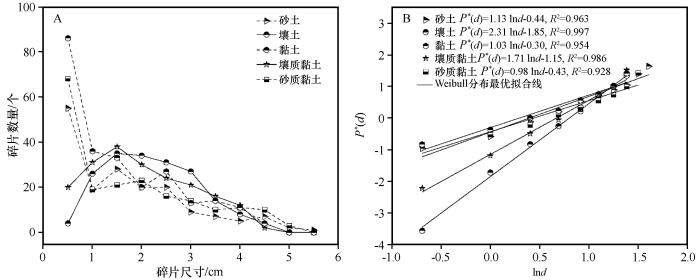
不同土壤碎片尺寸分布如图6A所示,壤土和壤质黏土碎片尺寸分布左倾,逐渐接近正态分布,粒径分布较为集中;砂土、黏土和砂质黏土接近于指数分布,分布相对分散,碎片主要集中在粒径1 cm以下。基于碎片尺寸分布,不同土壤类型团聚体碎片能够很好地服从Weibull分布,如图6B所示,这进一步表明单颗粒团聚体碰撞实验的有效性和合理性。分布函数中,β值与碎片分布分散性有关,其值越大,碎块粒径分布越集中。砂土、壤土、黏土、壤质黏土和砂质黏土β值分别为1.13、2.31、1.03、1.71、0.98。壤土和壤质黏土β值最大,接近β=2的标准Weibull分布,也称为Rayleigh分布,其概率密度函数近似正态分布;砂土、黏土和砂质黏土β值接近1,其概率密度函数近似指数分布,这与图6A分布基本一致。故不同模数的Weibull累积分布函数可以描述不同类型土壤的碎片尺寸分布。η为破碎程度参数,在断裂破碎研究中,其值可以反映材料断裂破碎的难易程度。碎片尺寸分布中表示累计粒度分布百分数达到50%时所对应的粒径,其反映碎片的中位粒径d50。砂土、壤土、黏土、壤质黏土和砂质黏土d50分别为1.48、2.23、1.34、1.96、1.55 cm,这表明大部分碰撞碎片的等效体积直径小于2.5 cm。
图6
图6
不同土壤团聚体碎片的碎片尺寸分布和Weibull分布
Fig.6
Fragment size distribution and Weibull distribution of different soil aggregates
3 结论
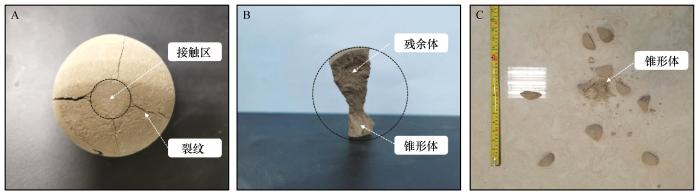
低速碰撞过程中,黏土、砂土、壤土、砂质黏土、壤质黏土5种土壤人工制备的球形团聚体破碎过程由无损状态过渡为损伤或者破碎状态,团聚体破碎状态主要是沿经线平面形成贯穿裂纹,在卸荷过程中产生较为对称的碎片,贯穿裂纹极少形成分叉或次生裂纹。较高速度下,接触区形成锥形体,锥形体周围形成次生裂纹,裂纹发散贯穿并爆破整个球体。
建立了土壤团聚体临界破碎速度与直径、密度、抗压强度和杨氏模量物理参数之间的经验公式。临界破碎速度拟合值与实验值相关性较好。
不同类型的土壤团聚体粉尘释放量有所差别。壤土粉尘释放量随速度变化显著,而黏土、砂土、砂质黏土、壤质黏土的粉尘释放量大部分小于团聚体质量的1%。壤土和砂土中掺杂黏土能有效改善其力学特征,减少粉尘释放量。
双参数Weibull分布函数能够描述碰撞破碎后团聚体的碎片尺寸分布规律。壤土和壤质黏土碎片尺寸分布接近模数为2的Weibull概率密度函数,而砂土、黏土和砂质黏土服从模数为1的分布。团聚体受内部微孔洞、微裂纹、杂质等局部缺陷影响,碰撞碎片分散性不同于玻璃、陶瓷等脆性材料。
参考文献
Wind erosion research in China:past,present and future
[J].
A simple expression for wind erosion threshold friction velocity
[J].
A new model for dust emission by saltation bombardment
[J].
Rate of wind abrasion on Mars
[J].
Erosion model for brittle materials under low speed impacts
[J].
A scaling theory for the size distribution of emitted dust aerosols suggests climate models underestimate the size of the global dust cycle
[J].
Midair collisions enhance saltation
[J].
On physically similar systems: illustrations of the use of dimensional equations
[J].
Size distribution functions for rock fragments
[J].
Three-parameter Weibull distribution with upper limit applicable in reliability studies and materials testing
[J].
Experimental study on the fragment characteristics of marble spheres under repeated impacts
[J].
Impact crushing of concrete for liberation and recycling
[J].
The statistical interpretation of the strength of float glass for structural applications
[J].
Silicon carbide-titanium diboride ceramic composites
[J].






 甘公网安备 62010202000688号
甘公网安备 62010202000688号