风沙沉积物搬运是地球环境地貌形成的主要因素^［1-4］。这种搬运导致沙尘气溶胶的排放，形成沙波纹和沙丘，并在很大程度上导致了沙漠化的蔓延。因此，准确预测风沙搬运过程及其地貌影响具有重要意义。风沙流内颗粒的3种运输方式，很大程度上取决于颗粒粒径d。一旦离开床面，粒径非常小（d ≲ 60 μm）的颗粒一般会以悬浮的方式被搬运，而直径大于500 μm的颗粒一般不会从地面扬起，但可以进行蠕移运动，即沿表面滚动或滑动。中等大小的颗粒通过跃移搬运，这包括在靠近地面跳跃的颗粒与沉积物床面碰撞时导致新颗粒的释放^［5-6］。跃移约占总输沙量的3/4^［1］，因而是风沙流中最重要的搬运模式。

典型的跃移运动可划分为起跳、上升、降落和冲击-溅起4个子过程。一般认为，饱和风沙流内气流对沙粒起跳和冲击-溅起两个子过程的影响可以忽略不计^［7-9］。而颗粒在上升段和降落段的平均速度随高度的变化则蕴含着气流与跃移沙粒相互作用的丰富信息，这是风沙跃移研究中的核心问题。在这一方面，需要同时测量不同高度的大量跃移颗粒的速度。其中，上升段与风沙颗粒释放过程相关，而降落段与风沙流的侵蚀性相关。由于与气流作用时间存在差异，颗粒上升和降落到某一高度的速度也必然存在差异。到目前为止，风沙物理学者们采用理论和实验的方法已对跃移颗粒平均速度随高度的变化做了大量的研究工作，然而，将颗粒在上升段与降落段进行分别讨论却鲜有报道。主要原因可能是将大量跃移颗粒的运动过程进行阶段划分在技术上还存在挑战。

风沙颗粒测速方法主要分为数值模拟和实验测量。自1985年Aarhus大学风沙物理学研讨会的启发性贡献后^［10-11］，跃移的数值模拟逐渐成为风沙研究中的活跃领域，极大地提高了人们对于跃移运动的理解。理论计算的精度取决于可用的初始条件（起跳速度和角度）、假设的有效性以及模型的简化程度。然而，风沙流内颗粒运动复杂， 牵涉沿风向加速度、气流的湍流波动、气流中颗粒间碰撞及颗粒对床面冲击等因素^［12］，马格努斯效应、萨夫曼升力和静电力等也在理论模型中难以考虑^［13-14］。因此，以目前对跃移物理机制的理解，数值模拟还无法满足跃移计算的要求，实验观测仍然是认识跃移运动规律的重要手段。

跃移颗粒速度的实验观测主要涉及两种方法：①基于激光多普勒方法的单点测量技术，例如粒子动力学分析仪（PDA）；②基于摄影方法的全流场测量技术，例如粒子图像测速技术（PIV）和高速摄影（HSP）。由于气流和颗粒速度都存在波动，单点测量虽然能在较短的时间内获得满足统计要求的数据量，但不能同步测量距沙床不同位置的颗粒速度^［15-17］，所得到的颗粒速度与高度关系的准确性还有待商榷。PIV方法通过互相关算法获得目标区域的平均速度，能同时满足数据量和同步观测的要求，但这种方法适用于粒子分布均匀的高浓度流场。然而，对于跃移沙粒，即使在很小的范围内，不同颗粒的速度也可能差异很大。因此，PIV给出的一个探测窗口内的平均速度，忽略了跃移粒子间速度的巨大差异性^［18］，难以对粒子运动过程进行细分（如上升段和降落段）。相比之下，HSP 技术可产生更平滑、几乎连续的颗粒图像序列并提供单个沙粒的可靠运动轨迹，并由此得到跃移颗粒在起跳、上升、降落以及粒-床碰撞等各阶段的速度特征。但HSP技术却难以获得具有统计意义的数据量。Zou等^［13］在风洞中使用高速摄影技术测量颗粒速度时检测到的最大样本颗粒数量仅为21个，在较大高度（50~60 mm）有时仅检测到一个颗粒，所得结果不符合大样本量的要求。

综上所述，各种测速手段均存在局限性。理论模型还不成熟、不能满足跃移运动计算的要求，单点测量技术（PDA）不能同步获得颗粒速度与所在高度的数据信息，PIV技术不能对跃移粒子的运动过程进行准确划分，而HSP技术在获取大量数据上存在困难。近年来，高速摄影技术（HSP）以及颗粒轨迹追踪技术的发展，使我们从高时间分辨率的沙粒运动图像序列中获得大量统计数据成为可能。本文通过自主开发的由简单的手动操作和计算机控制操作相结合的颗粒轨迹追踪技术^［9，19］获得了大量粒子在不同高度的数字化轨迹，进而获得了颗粒在上升段和降落段的速度信息，并以此为基础推导出颗粒在上升段和降落段的水平速度和垂直速度沿高度的变化形式，这对风沙物理学的研究有重要意义。

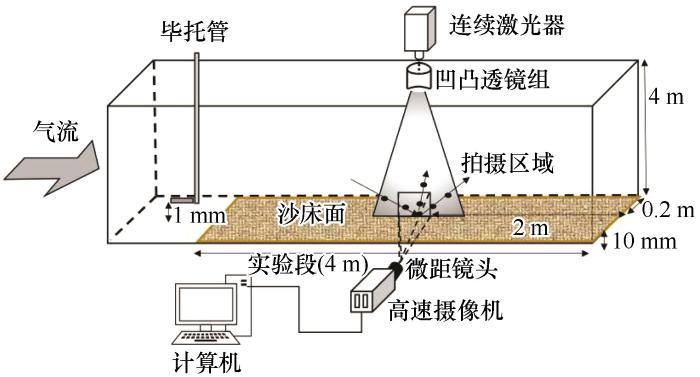
实验在中国科学院沙漠与沙漠化重点实验室的风沙环境风洞中进行。风洞总长10.5 m，测试段长4 m。测试段的横截面积为0.4 m×0.4 m。风洞中的自由风速可在1~35 m·s^-1调节。测试段的边界层厚度约为120 mm。图1为实验布置示意图。

用毕托管在实验段前端未铺设沙样的底面上方（约1 mm）可测得未受干扰的风速廓线。实验的主要目的是测量不同高度和自由流风速下不同大小跃移颗粒的平均速度。将人工打磨良好的密度为2.65×10³ kg·m^-3的干燥球形石英沙筛分为4个粒径组：0.1~0.2、0.2~0.3、0.3~0.4、0.4~0.5 mm。将准备好的沙样铺满整个测试段（厚度约为10 mm）以保证跃移充分发展。

测量开始前，先轻轻地将沙面刮平，并在风机打开后等待50~60 s使气流达到稳定后再进行拍摄。图像的捕捉区域设定在距离实验段口2 m处的风洞子午面位置。通过运用凹凸透镜组，将连续激光器所发射的532 nm激光光束转变为片光源。采用尼康短焦镜头（AF Micro Nikkor 60 mm f/2.8D，Nikon，东京，日本）与 Phantom V310高速数码相机（16 GB RAM，Vision Research Company，http：//www.visionre-search.com）所构成的高速摄影系统，获取到采集频率为每秒5 000帧、空间分辨率为800像素×600像素的沙粒运动图像序列。经过标定，图像的比例系数为每像素7.5×10⁻⁵ m。相机拍摄的目标区域大约为宽60 mm、高 45 mm。每次持续拍摄的时间约为5.6 s，从而获得28 000帧连续的图像序列。运用自主研发的轨迹追踪算法处理连续图像序列^［19］，得到一条条颗粒运动的数字化轨迹，从而获得给定高度的平均速度。

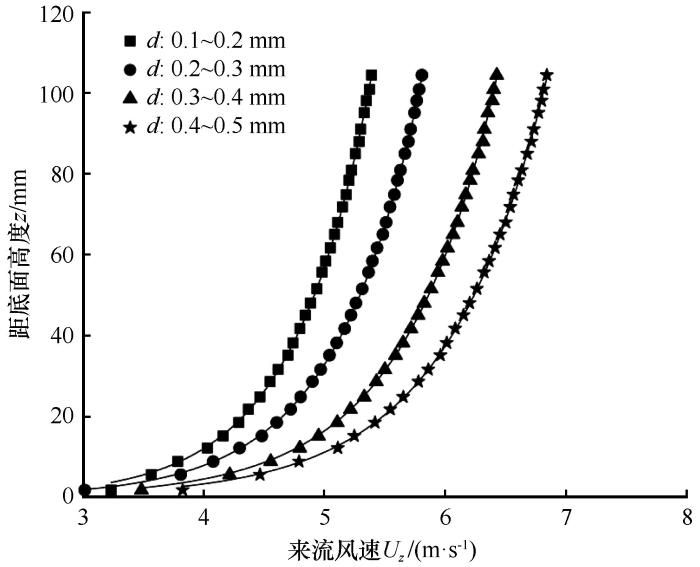
图2显示的风廓线可以用方程U_z=［u_*/κ］·ln（z/z₀）近似模拟，其中κ=0.4，为冯·卡门常数，z₀表示床面的有效粗糙度。通过对此方程进行拟合，可以得到摩阻风速（u_*）和粗糙度z₀。此外，我们在图2中看到，从约100 mm高度开始，风速随高度变化很小。因此，我们认为每个实验组中的平均自由风速（U）大约是对应于最大测量高度的风速值。由此得到，在实验中，4组沙样分别暴露在4个自由风速（U）下：5.5、5.9、6.5、6.9 m·s^-1，对应的摩阻风速（u_*）分别为 0.26、0.28、0.31、0.33 m·s^-1。床面的有效粗糙度（z₀）分别为0.0243、0.0260、0.0258、0.0261 mm。

颗粒的临界起动剪切风速（u_*t ）可通过式u_*t ≈0.1sgd估算，其中s为颗粒与流体的密度比，g为重力加速度，d为颗粒粒径。沙粒开始运输后维持持续运输的冲击阈值（u_*ti ）约为临界起动剪切风速（u_*t ）的80%^［1］。各组实验条件列于表1中。

风沙流中颗粒通过某一固定点的速度波动定义为颗粒湍流强度。颗粒湍流强度由风的湍流，颗粒-床面碰撞以及气流间颗粒的碰撞引起^［17］。湍流强度特征预示着均值的代表性。根据测量到的每个颗粒的瞬时速度，颗粒通过某一高度时的水平方向与垂直方向上的湍流强度可以根据式（1）被计算出来。由此，可分别分析湍流强度在水平方向和垂直方向随高度的变化特征。

式中：Tvx、Tvz分别是颗粒在水平方向和垂直方向的颗粒湍流强度；v¯x为平均水平速度，v¯z是平均垂直速度；vx,i是颗粒i的水平速度；vz,i为颗粒i的垂直速度；N为所测量的颗粒数。

为了使结果具有在不同实验条件下的适用性，在表征平均水平速度沿高度变化关系时，将涉及到的风速、颗粒速度和测量高度均进行了无量纲化处理：

式中：zr、ur、v¯rxzr分别为相对高度、相对高度zr处的相对风速、颗粒相对平均水平速度；Z为大气边界层厚度（120 mm）；g为重力加速度；d为沙粒粒径；u_*为摩阻风速；u_*ti 为维持跃移的冲击阈值。

由于颗粒在上升和降落过程中都可能会通过某一特定高度，我们将分别讨论颗粒轨迹在上升段和降落段颗粒的平均速度随高度的变化。判断的依据是在颗粒数字化轨迹中所在高度随时间增加的轨迹为上升段，反之为降落段。

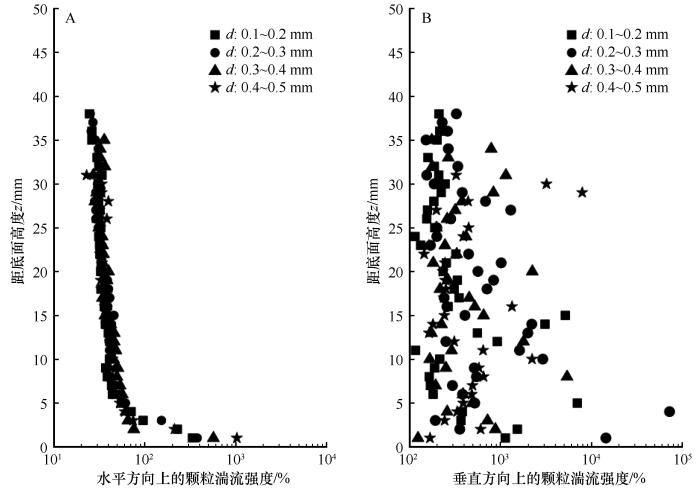
从图3A可以看到，4组实验沙样在水平方向上的颗粒湍流强度均在床面至3 mm高处呈急剧减小，而3 mm以上则随高度呈缓慢减小趋势，表明近床面的粒-床碰撞以及较大的空气湍流可能是颗粒水平湍流强度在床面至3 mm高处呈急剧减小的主要原因，而3 mm高度以上随高度减小的空气湍流可能起主导作用。图3B所示的垂直方向的颗粒湍流强度比水平方向上的颗粒湍流强度至少大1~2个数量级，最大值甚至接近1 000。这也表明颗粒在垂直方向上的湍流强度随高度变化非常复杂，没有明显的规律性。由于我们的实验是在较低的风速条件下进行，距床面3 mm以上高度气流中粒子间相互碰撞的概率不大，表明粒子与床面的碰撞可能是近床面颗粒产生垂直方向湍流强度变化的主要原因，而距床面3 mm以上高度，颗粒垂直方向上的湍流强度除了空气湍流影响外，可能还与颗粒旋转产生的升力、气流的拖拽力、自身的重力以及其他一些未知力的综合作用相关。

具有不同轨迹的跃移颗粒通过特定高度产生速度分布。在本文中，我们主要关注颗粒平均速度，但具有统计学意义的平均值必须从高质量的测量数据中获得，而这可以通过颗粒速度的分布模式来判断。通过颗粒轨迹追踪算法^［19］可以从高速摄影图像序列中获得大量颗粒的数字化轨迹，从而获得关于颗粒速度概率分布的丰富信息。然而，由2.1节计算的颗粒湍流强度可知，获取有统计学意义的颗粒平均垂直速度所需要的数据量要远大于颗粒平均水平速度，而颗粒数又随高度急剧减少。因此，根据我们的实验数据，对于水平速度统计的最大测量高度为27 mm，对于垂直速度统计的最大测量高度为18 mm。从床面开始以3 mm为一个高度区间进行统计。

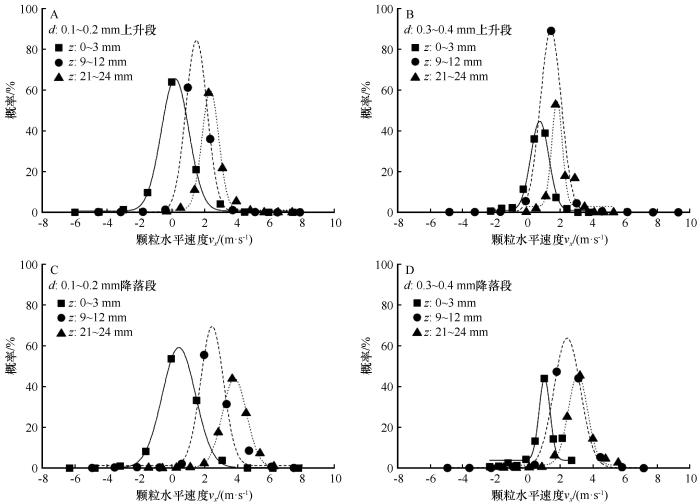
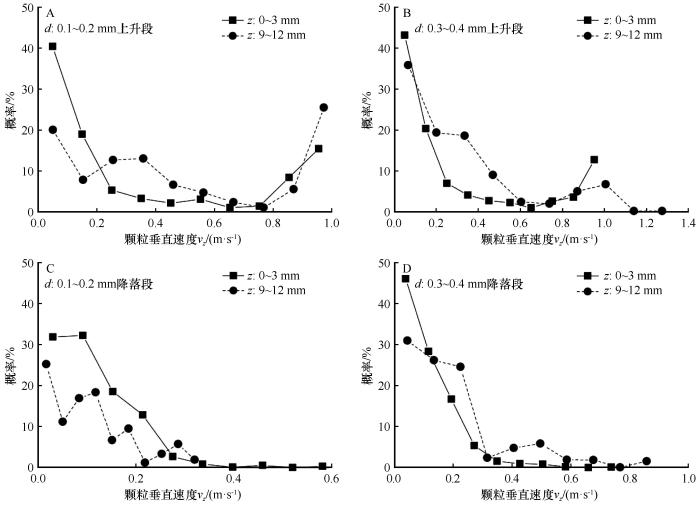
我们仅选择其中的一部分来展示不同尺寸组（0.1~0.2 mm和 0.3~0.4 mm）在不同高度（0~3、9~12、21~24 mm）下的速度分布。图4A、B和图4C、D分别显示了上升段和降落段颗粒水平速度的典型概率分布，图5A、B和图5C、D分别显示了颗粒上升段和降落段垂直速度的典型概率分布。颗粒在上升段和降落段的水平速度分布均很好地符合正态分布，这与前人整合上升段和降落段的研究结果相似^{［13.17，20-21］}。而上升段和降落段的颗粒由于在垂直方向上具有非常大的颗粒湍流强度（图3B），其垂直速度概率分布相对比较分散，但分布范围较窄（约0~1 m·s^-1）。因此，图4中颗粒水平速度的平滑概率分布模式，可以产生具有统计学意义的平均水平速度。而图5中颗粒垂直速度较小的变化范围对其统计平均值亦影响不大。

平均水平速度沿高度变化关系是评价风沙流动能变化的一个重要参数，因而也可确定风沙流侵蚀性沿高度的变化^［13］。尽管风沙研究者^{［13，17-18，20，22］}普遍认为水平平均颗粒速度随高度的变化有v¯x(z)=azb的幂函数增加趋势，且与风速大小成正比、与颗粒大小呈反比，但测量的结果仍存在较大差异。如Yang等^［18］使用PDA在近床面区域的测量结果普遍比Zou等^［13］使用高速摄影的测量结果大两倍以上，最大差异甚至超过6倍。

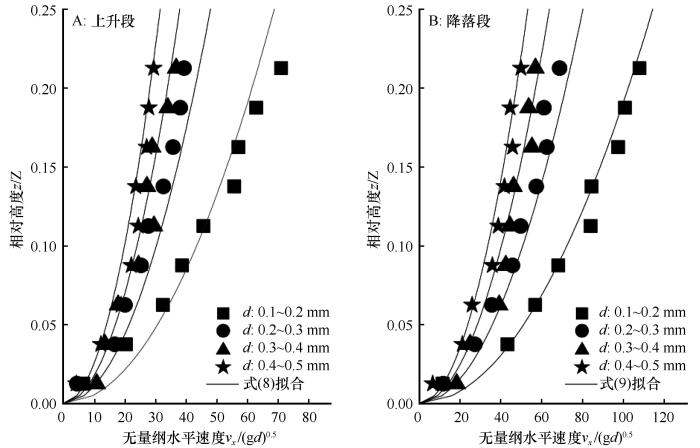
对图6所示的颗粒上升段和降落段的无量纲水平平均速度随高度的变化采用公式v¯rx(zr)=a(zr)b 进行最小二乘法拟合，结果表明，所有实验组的回归参数b均接近0.5。因此，上升段和降落段无量纲水平平均速度与相对高度可使用式（5）继续拟合：

各实验组使用式（5）拟合得到的回归系数aup和adown列于表2中。

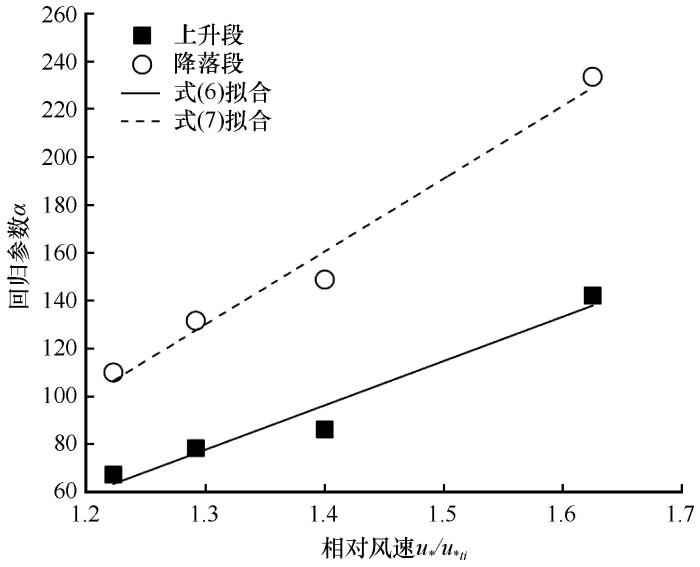
表2中的回归系数aup和adown分别是关于相对风速ur的函数，关系图如图7所示，关系方程分别为式（6）和式（7）。

结合式（5）~（7），分别得到了颗粒在上升段和降落段的无量纲平均速度与相对风速及相对高度的关系方程，即式（8）和式（9）：

由图6可知，式（8）和式（9）能很好地反映颗粒在上升段和降落段的无量纲平均速度随相对高度的变化关系。

式（8）和式（9）表明，颗粒平均水平速度随高度和风速增加而增加，但随颗粒尺寸减小而减小。

Dong等^［17］的PDA试验结果表明，多数情况下气流中沙粒的垂直速度比水平速度小1~2个量级。Yang等^［18］的PIV试验表明，平均垂直速度小于平均水平速度的4%。这些结论与本实验较为接近，不同的是，他们都考虑的是颗粒的整个运动过程，没有划分上升段与降落段进行单独分析。理论上讲，颗粒的垂直速度应随高度按式（10）变化：

式中：vp(z)是颗粒在高度z处的垂直速度；vp0颗粒垂直起跳速度；g是重力加速度。

事实上，由于床面的反弹、气流中颗粒间的碰撞^［23-24］、空气湍流引起的升力、马格努斯力以及一些其他未知的因素，颗粒垂直速度的变化远比式（10）复杂。垂直方向上较大的颗粒湍流强度（图3B）也反映了垂直速度的复杂性。

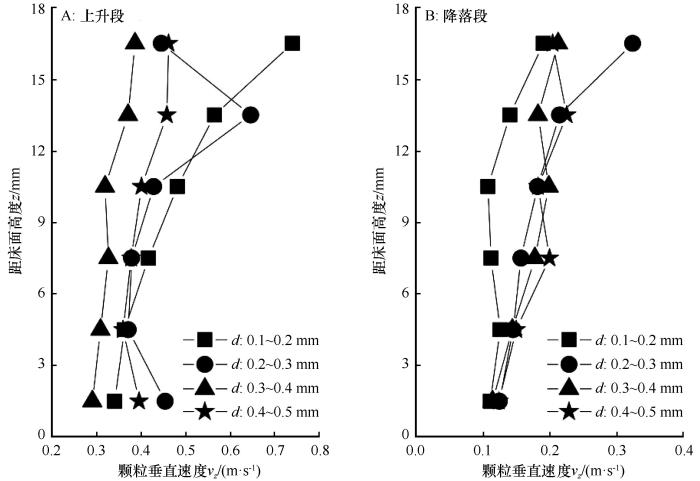
从图8A可以看到，上升段的颗粒垂直平均速度随高度有缓慢的增加趋势，在贴近床面区域，其大小接近水平平均速度，但平均水平速度随高度呈幂指数增加（图6A），因此，随高度增加垂直速度与水平速度的差距越大，在测量的最高点处，相差接近10倍。在降落段，随着颗粒接近床面，垂直平均速度逐渐减小并趋于一个定值，这个定值约是0.12 m·s^-1（图8B）。Shao等^［25］曾报道了风洞中跃移运动的“靶”（overshoot）现象。图8B中各垂直平均速度沿高度变化曲线更像是靶点的分支。对比图8A和图8B，上升段的平均垂直速度主要在0.3~0.7 m·s^-1变化，而降落段的平均垂直速度主要在0.1~0.3 m·s^-1变化，表明上升段的垂直平均速度略高于降落段。垂直平均速度随高度变化的深入理解还需要进一步研究。

我们通过颗粒轨迹追踪算法与高速摄影技术（HSP）的结合获得了风洞中大量跃移粒子的数字化轨迹，将粒子运动过程细分为上升段和降落段并分别分析了颗粒速度随高度的变化特征。大量的样本数量确保了颗粒平均速度具有统计学意义。

主要结论如下：①水平方向上的颗粒湍流强度在床面至3 mm高处呈急剧减小，而3 mm以上则随高度呈缓慢减小趋势，表明空气湍流可能是引起水平方向上颗粒湍流强度变化的主要原因。垂直方向上的颗粒湍流强度比水平方向高1~2个数量级，且随高度变化非常复杂，没有明显的规律性。②水平速度服从正态分布，而垂直速度则分布分散且变化范围较窄（0~1 m·s^-1）。③上升段和降落段的平均水平速度均与高度的平方根以及相对风速（u_*/u_*ti ）成正比。降落段的平均水平速度约是上升段的1.6~1.8倍。④上升段和降落段的颗粒垂直平均速度均随高度有缓慢的增加趋势，上升段的垂直平均速度略高于降落段。

一般来说，水平平均速度与高度具有很好的相关性，而垂直速度随高度的变化特征还需进一步深入研究。