基于标准化地下水指数的酒泉绿洲地下水干旱特征

doi:10.7522/j.issn.1000-694X.2024.00093

基于标准化地下水指数的酒泉绿洲地下水干旱特征

王楠^,^1a, 吴丽丽^,^1b, 温小虎^,², 杨林山², 尹振良², 方锦杰³

1a.甘肃农业大学，理学院，甘肃兰州 730070

1b.甘肃农业大学，信息科学技术学院，甘肃兰州 730070

2.中国科学院西北生态环境资源研究院，甘肃兰州 730000

3.兰州大学数学与统计学院，甘肃兰州 730000

Drought characteristics of groundwater in Jiuquan Oasis based on the standardized groundwater index

Wang Nan^,^1a, Wu Lili^,^1b, Wen Xiaohu^,², Yang Linshan², Yin Zhenliang², Fang Jinjie³

1a.College of Science /, Gansu Agricultural University，Lanzhou 730070，China

1b.College of Information Science and Technology, Gansu Agricultural University，Lanzhou 730070，China

2.Northwest Institute of Eco-Environment Resources，Chinese Academy of Sciences，Lanzhou 730000，China

3.School of Mathematics and Statistics，Lanzhou University，Lanzhou 730000，China

通讯作者: 吴丽丽（E-mail： Wull@gsau.edu.cn）温小虎（E-mail： xhwen@lzb.ac.cn）

收稿日期: 2024-06-06 修回日期: 2024-10-10

基金资助:

中国科学院先导项目.  XDB0720202
黄河流域生态保护和高质量发展联合研究一期项目.  2022-YRUC-01-0601
中国科学技术协会青年人才托举工程项目.  YESS20200089
中国科学院青促会会员项目.  2022435

Received: 2024-06-06 Revised: 2024-10-10

作者简介 About authors

王楠（2000—），女，河北人，硕士研究生，从事人工智能与数据挖掘研究E-mail：wangyaya171@163.com , E-mail：wangyaya171@163.com

摘要

地下水干旱不仅严重制约着区域的社会经济发展，还给地下水资源管理带来了巨大挑战。以酒泉绿洲为例，根据11个观测井1985—2017年的月地下水位数据，选用6种概率分布函数构建了标准化地下水指数（Standardized Groundwater Index， SGI），并利用K-S检验（Kolmogorov-Smirnov test）和AIC准则（Akaike information criterion）进行分布函数的优选。结果表明：Gev分布和Beta分布在不同时间尺度上均展现出较强的适用性。采用K-Means聚类法将11个观测井的SGI分为持续下降型、下降-上升型以及2002—2006年发生突变型。STL（Seasonal and Trend decomposition using Loess）分解结果显示，持续下降型观测井的地下水干旱情况由非干旱持续恶化成中度-重度干旱，下降-上升型观测井的地下水干旱情况不显著，2002—2006年发生突变型观测井在经历突变后，地下水干旱情况长期维持在中度-重度水平。此外，地下水观测井SGI的季节峰值集中在冬季的12、2月和春季的3、5月。

关键词： 地下水干旱 ; 标准化地下水指数 ; K-Means聚类 ; STL分解 ; 酒泉绿洲

Abstract

Groundwater drought not only severely restricts the socioeconomic development of the region， but also brings great challenges to groundwater resource management. Therefore， in this study， taking Jiuquan Oasis as an example， six different probability distribution functions were selected to construct the standardized groundwater index （SGI） by analysing the monthly groundwater level data of 11 observation wells from 1985 to 2017， and the K-S test and the AIC criterion were used for the preference of the distribution functions. The results show that the Gev function and the Beta function show strong applicability in different time scales. Based on this， this paper adopts K-Means clustering method to classify the SGI of 11 observation wells into three categories： continuously declining type， declining-rising type， and mutation type between 2002 and 2006. The results of the decomposition show that the groundwater drought condition of the "Continuously declining" wells deteriorated from non-drought to moderate-severe drought， the “Declining-rising” wells had insignificant groundwater drought conditions， and the "Mutation between 2002 and 2006" wells maintained the groundwater drought condition at the moderate-severe level for a long period of time after experiencing the mutation. In addition， the seasonal peaks of SGI in groundwater observation wells were concentrated in December and February in winter and in March and May in spring. The results of the study provide a basis for the scientific management of groundwater resources in the Jiuquan oasis.

Keywords： groundwater droughts ; standardized groundwater index ; K-Means clustering method ; seasonal-trend decomposition using LOESS method ; Jiuquan Oasis

PDF (4692KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王楠, 吴丽丽, 温小虎, 杨林山, 尹振良, 方锦杰. 基于标准化地下水指数的酒泉绿洲地下水干旱特征. 中国沙漠[J], 2025, 45(1): 121-130 doi:10.7522/j.issn.1000-694X.2024.00093

Wang Nan, Wu Lili, Wen Xiaohu, Yang Linshan, Yin Zhenliang, Fang Jinjie. Drought characteristics of groundwater in Jiuquan Oasis based on the standardized groundwater index. Journal of Desert Research[J], 2025, 45(1): 121-130 doi:10.7522/j.issn.1000-694X.2024.00093

0 引言

地下水对干旱和半干旱区的绿洲发展和人类生存至关重要，它提供了约50%的饮用水、40%的工业用水及20%的农业灌溉供水^［1］。然而，随着人类需求的增长，地下水资源短缺问题加剧^［2］。干旱是具有长期性、广泛性和破坏性的自然灾害^［3-4］，一般可分为气象干旱、水文干旱、农业干旱以及社会经济干旱4类^［5］。近年来，地下水干旱备受关注，有学者认为地下水位降低、地下水储量减少，进而导致地下水资源短缺的现象即为地下水干旱^［6］，其隐蔽性强、持续时间长、滞后性明显，对农业、生态环境以及社会经济构成严重威胁^［7-8］。因此，加强对干旱和半干旱区地下水干旱特征的认识，对于干旱风险评估和水资源的规划管理具有重要意义。

早期对地下水干旱的研究多基于实测数据或模型模拟的地下水位数据，目的在于构建相关指数以描述地下水的干旱状况^［9-10］，如借鉴标准化降水指数（Standardized Precipitation Index， SPI）的构建方法，通过非参数正态得分变换，构建标准化地下水指数（Standardized Groundwater Index， SGI）^［11］。由于地下水系统受地质、气候和人类活动等因素影响，地下水位数据呈现长期趋势和季节性波动，因此，拟合函数的选择对SGI的评价结果至关重要，不同的拟合函数可能导致不同的评价结果，合适的概率分布函数可以更有效地反映地下水位的变化特征^［12-13］。传统的地下水干旱指数构建方法，如基于水量平衡的方法^［14］、利用原位地下水观测数据的统计应用或水文模型模拟^［15-16］，受限于监测井空间分布的不均匀性。随着遥感技术的发展，基于NASA重力恢复和气候实验（GRACE）卫星观测数据的地下水干旱研究因其全球观测分布均匀且不受地面观测站点的限制等优势，为地下水干旱研究提供了全新视角^［17-18］，但目前由于长时间序列地下水位数据的缺乏以及GRACE卫星观测数据在空间、时间分辨率上的局限性^［19］，一定程度上制约了其在地下水干旱领域的应用。因此，对于小尺度区域、具备长时序观测的地下水位数据而言，SGI依然是研究地下水干旱的有效指标。

酒泉盆地是河西走廊重要的商品粮和农作物种植基地，也是中国西北重要的农业灌溉区^［20］。该地区由于独特的地质构造拥有丰富的含水层，地下水系统的补给主要依赖祁连山河水的渗透^［21］。然而，干旱大陆性气候导致该地区年降水量稀少，蒸发量大，地表水资源有限，地下水成为了支撑绿洲农业发展的宝贵资源。近年来，随着农业和工业的快速发展，酒泉盆地的用水需求急剧增加，给地下水资源管理带来了巨大压力^［22］。鉴于此，本研究选取酒泉绿洲作为研究区，利用最优拟合分布函数构建SGI，以探究该地区的地下水干旱特征，同时，采用STL法（Seasonal and Trend decomposition using Loess， STL）将SGI序列进行分解，以揭示地下水位的长期趋势和季节性变化规律。

1 数据与方法

1.1　数据与研究区概况

本研究选取酒泉绿洲内11个地下水观测井1985—2017年的月地下水位数据（图1）。酒泉绿洲位于甘肃省西北部河西走廊西端，北接巴丹吉林沙漠与内蒙古接壤，南靠祁连山脉与青海相连，属于典型的大陆性干旱气候^［23］。年平均气温为5.8~10 ℃，年降水量为117.5 mm，集中在6—8月，年潜在蒸发量为2 148.8 mm。观测井所在的流域总面积约2.81万km²，主河道全长370 km，多年平均径流量为6.37亿m³，地下水资源总量为7.79亿m^3［24］。

图1

新窗口打开| 下载原图ZIP| 生成PPT

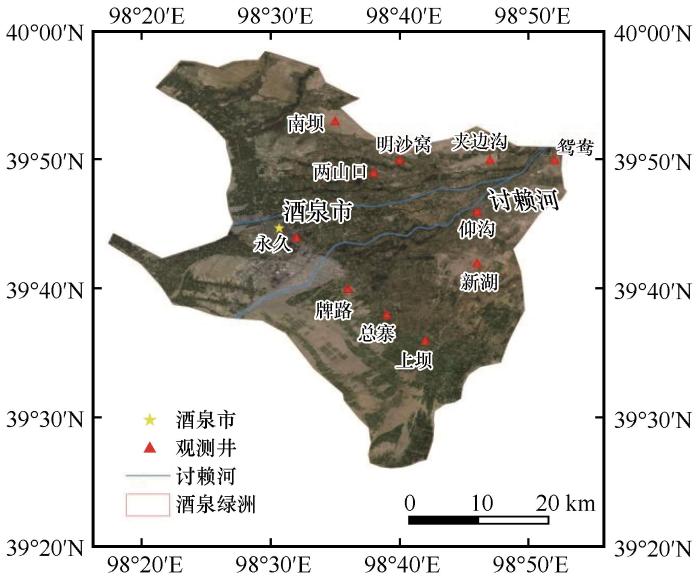
图1 酒泉绿洲11个地下水观测井的分布

Fig.1 Distribution map of 11 groundwater observation wells in Jiuquan Oasis

酒泉绿洲农田防护林主要依靠灌溉生存^［25］，灌溉水源主要来自讨赖河引水和地下水。讨赖河河水渗透到地下，形成地下水资源^［26］，地下水在酒泉盆地细土平原顶部出露，形成泉水。从地质条件来看，酒泉盆地西临嘉峪关断裂和文殊山隆起，东接高台隆起。受多次构造运动的影响，南部祁连褶皱带与戈壁平原被格尔木断裂、狼尾山-牛头山断裂以及河西走廊南缘深大断裂分隔。此外，盆地南部白垩纪—第三纪地层的阻隔导致山区与戈壁平原形成了两个独立的地下水系统^［27］，山区前沿的大断裂阻碍了山区基岩裂隙水向戈壁平原的补给。因此，从戈壁平原到细土平原，酒泉盆地形成了完整的补给、径流、排泄水文地质单元，含水层从单一的厚层砂砾石含水层过渡到双层或多层细粒含水层，厚50~400 m，内部含有丰富的第四纪松散沉积物^［28］。地下水位自西南向东北逐渐变浅，南部山前地带的地下水深超过100 m，盆地中部为20~40 m，讨赖河出口处则小于10 m。

1.2　研究方法

1.2.1　SGI的计算

参数化方法构建SGI^［29］。选取6种拟合分布函数——对数正态（lgN）分布、极值（EV）分布、广义极值（GEV）分布、伽马（Gamma）分布、贝塔（Beta）分布和威布尔（Weibull）分布对原地下水月平均水位序列 $x_{0_{i}}$ 进行归一化处理，得到新序列 $x_{i}$ ：

x_{i} = \frac{x_{0_{i}} - m i n (x_{0_{i}})}{m a x (x_{0_{i}}) - m i n (x_{0_{i}})}

（1）

然后，对归一化后的序列进行参数拟合，求得拟合分布的累积频率分布 $F_{\begin{matrix} x, j \end{matrix}}$ ：

F_{x, j} = \int_{- \infty}^{x} f_{x, j} (t) d t

（2）

式中：j=1，2，3，4，5，6，对应6种拟合分布函数。最后，逆标准化 $F_{x, j}$ ，得到SGI值：

S G I_{j} = Φ^{- 1} (F_{x, j})

（3）

非参数化方法构建SGI。首先，将原地下水月平均水位序列 $x_{0_{i}}$ 排序得到新序列 $x_{1_{i}}$ ；其次，将新序列 $x_{1_{i}}$ 在区间 $(\frac{1}{2 n} ~ 1 - \frac{1}{2 n})$ 内等分并赋概率值 $P_{i}$ ：

P_{i} = \frac{1}{2 n} + \frac{i - 1}{n} (i = 1,2, \dots, n)

（4）

接着，逆标准化 $P_{i}$ 得到 $S G I_{i}$ 值：

S G I_{i} = ϕ^{- 1} (P_{i})

（5）

最后，将 $S G I_{i}$ 值重新按时间排序，得到非参数化的 $S G I$ 值。

利用SGI进行地下水干旱的识别，旨在准确评估地下水干旱的严重程度，SGI值与地下水干旱等级的对应关系如表1所列^［30］。

表1 SGI 的干旱识别

Table 1 Drought tecognition at SGI

SGI取值区间	干旱等级
$S G I > 0.0$	非干旱
$- 1.0 < S G I \leq 0.0$	轻度干旱
$- 1.5 < S G I \leq - 1.0$	中度干旱
$- 2.0 < S G I \leq - 1.5$	重度干旱
$S G I \leq - 2.0$	极端干旱

新窗口打开| 下载CSV

1.2.2　最优拟合分布函数的检验方法

K-S检验（Kolmogorov-Smirnov Test）^［31］通过比较实际样本数据的累积分布函数（ $F_{2 (x)}$ ）与理论分布的累积分布函数（ $F_{1 (x)}$ ）之间的最大差距 $D$ 来评估两者之间的相似性。

D = m a x | F_{1 (x)} - F_{2 (x)} |

（6）

在显著性水平 $α$ （ $α$ =5%）下，若D>D（n， $α$ ）（n为样本容量），就有理由拒绝原假设，即认为样本分布函数与理论分布函数之间存在显著差异。

AIC准则^［32］（Akaike information criterion）是一种基于信息论的模型拟合优度评估方法，综合考虑了模型的复杂度和拟合程度，通过比较实际值与预测值的差异来选择最佳模型，AIC值最小即为最佳。

A I C = 2 k - 2 l n (L)

（7）

式中：k是模型参数的数量；L是似然函数值。

拟合分布函数的优选步骤。首先，对每个地下水观测井的6种函数拟合结果进行K-S检验，以判断其是否适用于拟合SGI，若K-S检验通过，则认为该函数可以用于拟合SGI。若通过K-S检验的函数种类唯一，则视该函数为最优拟合函数；若6种函数均未通过K-S检验，则采用非参数化方法构建SGI；若通过K-S检验的函数种类不唯一，则需要进一步计算AIC值，视AIC值最小的函数为最优拟合函数。

1.2.3　时空分析方法

K-Means聚类法。K-Means聚类是无监督学习算法，通过迭代分配数据点至最近的簇中心并更新中心位置，直至中心稳定或达到预设的迭代次数^［33］，聚类过程中使用平方欧几里得距离（SED）衡量观测井之间的相似性。优化目标是最小化每个点到簇中心的平方误差总和A，以确定数据点的簇归属。

A = m i n \sum_{i = 1}^{k} \sum_{x \in k_{i}} {|| x_{k} - m_{i} ||}^{2}

（8）

式中： $x_{k} = (x_{1}, x_{2}, \dots, x_{n})$ 是属于 $k_{i}$ 簇的数据； $m_{i}$ 是 $k_{i}$ 类的质心。

STL法。STL法（Seasonal and Trend decomposition using Loess）是水文时间序列分解中通用且稳健的方法^［34］，该方法利用局部加权回归技术LOESS（Locally Estimated Scatterplot Smoothing），通过自适应加权每个数据点的邻域精准捕捉时间序列的局部结构，将其分解为趋势、季节性和残差3个核心分量^［35］：

Y_{t} = T_{t} + S_{t} + R_{t}

（9）

式中： $Y_{t}$ 、 $T_{t}$ 、 $S_{t}$ 和 $R_{t}$ 分别表示原始时间序列数据、趋势分量、季节分量和残差分量。 $T_{t}$ 反映时间序列的长期增减趋势， $S_{t}$ 揭示周期性波动， $R_{t}$ 包含随机波动和异常值，体现非周期性特征。

趋势强度（ $F_{t}$ ）反映SGI随时间的长期变化显著程度，季节强度（ $F_{s}$ ）则衡量SGI在每月这一特定时间周期内的周期性波动幅度，这一指标与地下水位的季节性变化紧密相关，残差代表了SGI变化中未被趋势和季节性分量所解释的部分，反映了SGI变化的不稳定性和随机性。

F_{t} = m a x [0,1 - \frac{V a r (R_{t})}{V a r (T_{t} + R_{t})}]

（10）

F_{s} = m a x [0,1 - \frac{V a r (R_{t})}{V a r (S_{t} + R_{t})}]

（11）

2 不同时间尺度下SGI的最优拟合分布函数

2.1　不同时间尺度下SGI的K-S检验通过率和拟合函数优选率

SGI-1（1月尺度）反映干旱特征的月度变化；SGI-3（3月尺度）反映干旱的季节性特征，通常与农业地下水干旱密切相关；SGI-6（6月尺度）和SGI-12（12月尺度）在长期尺度上反映干旱变化的特征，更适合描述地下水干旱的长期趋势变化^［35］。

由表2可知，Gev分布和Beta分布在不同时间尺度上均具有较高的通过率，6种拟合函数的K-S检验通过率均随时间尺度增大而提高。由于地下水位月度数据分布特性复杂且易受极端天气导致的极端值的影响，在使用概率分布函数进行拟合时误差显著，导致SGI-1的K-S检验通过率普遍偏低，最高通过率仅为36.36%。

表2 6种拟合函数在不同时间尺度下的K-S检验通过率 (%)

Table 2 K-S test pass rates for the six fitting functions at different time scales

时间尺度	拟合函数
时间尺度	lgN	Ev	Gev	Gamma	Beta	Weibull
SGI-1	0.00	18.18	36.36	0.00	36.36	18.18
SGI-3	0.00	72.73	81.82	18.18	54.55	63.64
SGI-6	9.09	72.73	81.82	36.36	81.82	63.64
SGI-12	54.55	90.91	90.91	72.73	81.82	72.73

新窗口打开| 下载CSV

K-S检验结合AIC准则进一步反映了拟合函数的优选率。由表3可知，Gev分布在1、3、6、12月尺度下的优选率分别为66.67%、66.67%、44.44%和0；Beta分布在1、3、6、12月尺度下的优选率分别为50.00%、50.00%、55.56%和100.00%；而lgN分布和Gamma分布在该研究区的优选率始终为0。Gev分布和Beta分布在各个时间尺度上的优选率均高于其他分布，这显示了其在酒泉绿洲地区的适用性。

表 3 6种拟合函数在不同时间尺度下的优选率 (%)

Table 3 Preferences of six fitting functions at different time scales

时间尺度	拟合函数
时间尺度	lgN	Ev	Gev	Gamma	Beta	Weibull
SGI-1	0.00	0.00	66.67	0.00	50.00	14.29
SGI-3	0.00	0.00	66.67	0.00	50.00	14.29
SGI-6	0.00	12.50	44.44	0.00	55.56	0.00
SGI-12	0.00	0.00	0.00	0.00	100.00	12.50

新窗口打开| 下载CSV

2.2　最优拟合函数的确定

鉴于同一地区在不同时间尺度下地下水干旱的严重程度存在差异，合理选取适用于不同时间尺度的最优SGI拟合分布函数至关重要。1月尺度下最优拟合函数的分布结果如表4所列，非参数方法更适合SGI-1的计算，Gev分布也具有一定适用性。进一步确定3、6、12月尺度下的最优拟合函数（表5）。3月尺度下，Gev分布具有明显优势，即Gev分布在较短时间尺度内能较好地拟合酒泉绿洲的地下水位变化；6月尺度下，Gev和Beta分布都有较好的适用性；12月尺度下，Beta分布的优势更加明显，即Beta分布能更好地拟合酒泉绿洲地下水位的长期变化情况。

表4 SGI-1最优拟合函数的选取

Table 4 Selection of the optimal fitting function for SGI-1

观测井名称	拟合函数						最优拟合函数
观测井名称	lgN	Ev	Gev	Gamma	Beta	Weibull	最优拟合函数
夹边沟	0/323.42	0/-46.98	0/-49.94	0/131.45	0/-44.48	0/42.55	非参数
两山口	0/-1 355.99	0/-312.84	0/-1 541.62	0/-1 477.33	0/-1 176.65	0/-1 388.76	非参数
明沙窝	0/125.13	0/-104.65	1/-138.95	0/-31.48	0/-77.72	0/-111.29	Gev
南坝	0/-111.29	0/284.08	0/73.47	0/37.66	0/153.93	0/99.17	非参数
牌路	0/230.44	0/-88.09	1/-116.26	0/33.19	1/-99.33	1/-64.44	Gev
上坝	0/111.52	0/110.08	0/12.99	0/16.61	0/-30.81	0/-2.89	非参数
新湖	0/393.68	0/72.67	0/34.21	0/188.46	1/-13.12	0/119.13	Beta
仰沟	0/206.90	0/-352.19	0/-346.10	0/-41.77	0/-272.49	0/-244.92	非参数
永久	0/163.55	1/-172.01	0/-194.49	0/-50.35	0/-153.29	0/-154.05	Ev
鸳鸯	0/94.09	0/-84.76	1/-125.89	0/-47.96	1/-74.50	0/-105.74	Gev
总寨	0/180.38	1/-183.30	1/-202.89	0/-33.06	1/-170.34	1/-149.76	Gev

注：通过K-S检验为1，未通过K-S检验为0。

新窗口打开| 下载CSV

表5 观测井的SGI在不同时间尺度下的最优拟合函数

Table 5 Best-fit functions of SGI for each well at different time scales

观测井名称	时间尺度
观测井名称	SGI-3	SGI-6	SGI-12
夹边沟	Gev	Ev	Beta
两山口	非参数	非参数	Beta
明沙窝	Gev	Gev	非参数
南坝	Beta	Beta	Beta
牌路	Gev	Beta	Beta
上坝	Weibull	Beta	Beta
新湖	Beta	Beta	Beta
仰沟	Gev	Gev	Beta
永久	Gev	Gev	Beta
鸳鸯	Beta	Beta	Beta
总寨	Gev	Gev	Weibull

新窗口打开| 下载CSV

3 SGI的时空变化特征

SGI-3、SGI-6以及SGI-12虽具有明显的优势拟合分布，但长时间尺度的数据平滑处理不可避免地削弱了重要的短期波动信息，而SGI-1与长时间尺度的SGI在趋势性和季节性上保持高度一致，且其记录了逐月数据信息，充分代表了SGI的总体趋势及年度季节性变化。因此，本节针对SGI-1进行K-Means聚类和STL时间序列分解，以探讨SGI的时空变化特征。

3.1　空间聚类

采用K-Means聚类法，SGI-1数据作为聚类变量，依据SGI变化趋势将观测井划分为3类：持续下降型、下降-上升型以及2002—2006年发生突变型（图2）。

图2

新窗口打开| 下载原图ZIP| 生成PPT

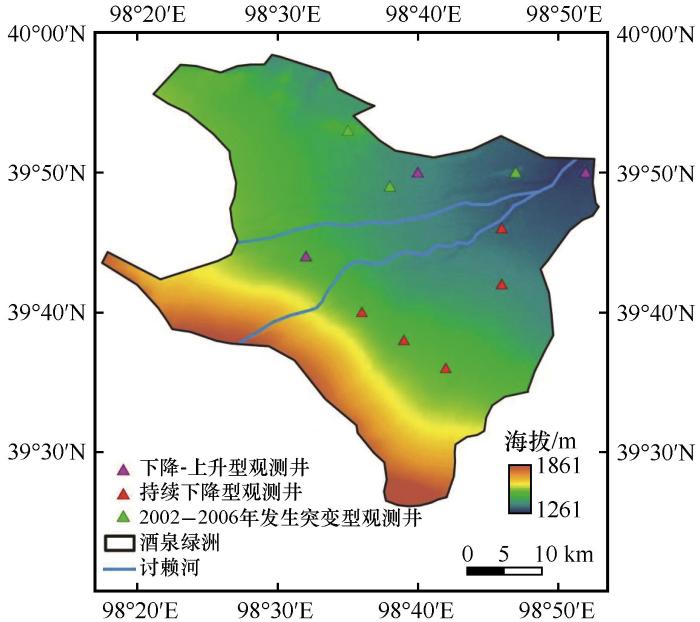
图2 根据K-Means聚类划分观测井类型的空间分布

Fig.2 Spatial distribution of observation wells classified according to K-Means clustering

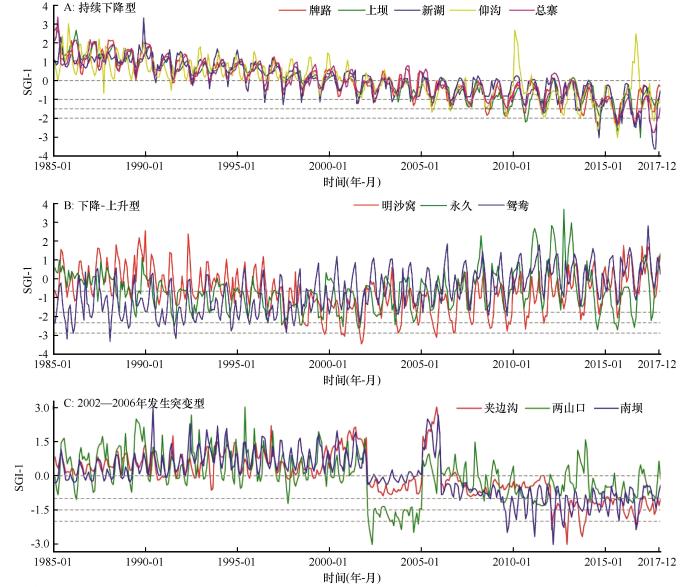
结合图2、3，观察到不同类别观测井的干旱特征各异。讨赖河南部支流的观测井（牌路、上坝、新湖、仰沟、总寨）表现为持续下降型，SGI-1值为-4.0~3.0，并随时间下降。自2001年起，其SGI-1<0，地下水开始趋向干旱，2001—2017年在轻度干旱至中重度干旱波动。讨赖河北部支流的观测井（明沙窝、永久、鸳鸯）呈现下降-上升型变化。1985—2002年，明沙窝和永久的SGI-1值逐渐下降，地下水由非干旱转向轻至中度干旱，鸳鸯在1999年之前大多表现为轻度干旱。自2002年起，SGI-1值回升，特别是在2010—2017年多数时间SGI-1>0，干旱状况有所缓解，地下水逐渐恢复。2002—2006年发生突变型的观测井（夹边沟、两山口、南坝），SGI-1值在2002年前表现为非干旱，但随后急剧下降，夹边沟和南坝出现轻度干旱，两山口则恶化至重度甚至极端干旱。尽管2005—2006年SGI-1值短暂回升至非干旱状态，但2006—2017年再次趋向干旱，且干旱程度较突变前更为严重。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 最优拟合分布下SGI-1的聚类结果

Fig.3 Clustering results of SGI-1 under the best-fit distribution

持续下降型观测井因远离河水，地表水补给匮乏，加之灌溉面积扩张，灌溉期过度抽取地下水，导致讨赖河南部SGI-1持续下降，干旱加剧。下降-上升型观测井与南部支流形成鲜明对比，1985—2002年SGI-1下降受当时灌区灌溉设施老化导致的渗漏大、输水能力差的影响；2002年后SGI-1值的上升主要得益于水库与河流对地下水的补给作用（明沙窝井靠近夹边沟水库、永久井位于文殊沙河边、鸳鸯井靠近鸳鸯池水库），以及节水灌溉技术如喷灌、滴灌的普及应用。2002—2006年发生突变型观测井在地理位置上呈现出独特性和局部性，其SGI-1的变化趋势受多种因素影响：2002年，该地区重点培育“五大产业”，加快发展特色农业，特别是肃州区的奶牛养殖和制种产业推动了粮食作物、饲草作物和造林面积的显著增长，产业结构的调整使得水资源过度利用，导致SGI-1突然下降^［36］；随后，2004年造林面积骤降71%，2005年渔业生产下滑，造林面积再降22.70%，同时保证灌溉面积减少1.20万hm²，使得SGI-1在2005年年初显著上升^［37］；2005—2006年，牛存栏量下降11.8%，在此期间，种植结构的持续调整以及降水分布的不均匀导致SGI-1值的不稳定^［38］；然而，自2006年起，种植结构逐渐稳定，水资源管理和利用也趋于合理，SGI-1值逐渐趋向平稳。

3.2　STL分解结果

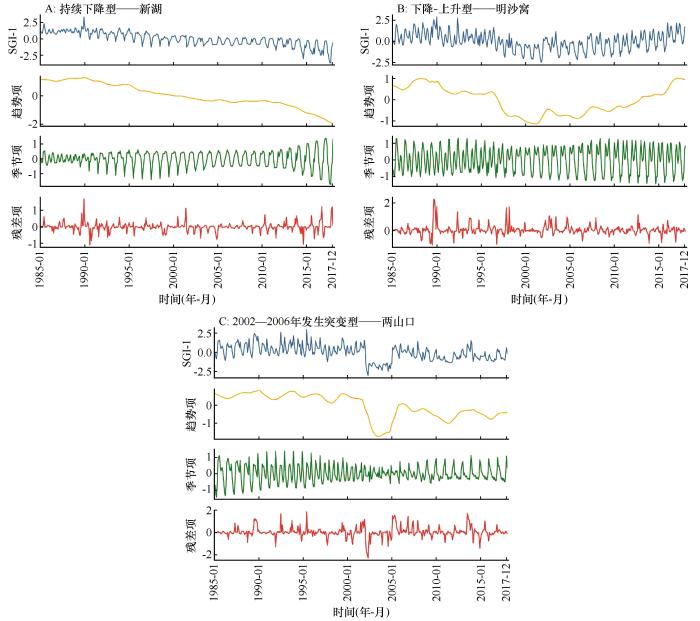
将11个观测井的SGI-1进行STL分解，得到其趋势项、季节项和残差项，选取3个代表井展示分解结果。

图4中3个代表井的趋势变化与3.1节讨论的聚类结果一致。剔除季节性和残差影响后，趋势项曲线更为平滑：持续下降型观测井趋势项持续走低；下降-上升型观测井呈现先降后升的明显特征；而2002—2006年发生突变型观测井在指定年份间经历显著突变，其余时段保持相对稳定。表6数据显示，11个地下水观测井的趋势强度均超过0.6，表明其长期变化趋势显著。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 代表井的STL分解结果

Fig.4 STL decomposition results for representative wells

表 6 SGI-1的趋势强度、季节强度及季节峰值

Table 6 Trend intensity， seasonal intensity and seasonal peak of SGI-1

指标	观测井名称
指标	夹边沟	两山口	明沙窝	南坝	牌路	上坝	新湖	仰沟	永久	鸳鸯	总寨
趋势强度	0.842	0.699	0.749	0.774	0.914	0.951	0.899	0.683	0.671	0.841	0.953
季节强度	0.187	0.520	0.773	0.480	0.766	0.774	0.767	0.401	0.756	0.861	0.832
季节峰值	5月	11月	5月	5月	2月	3月	12月	12月	2月	5月	3月

新窗口打开| 下载CSV

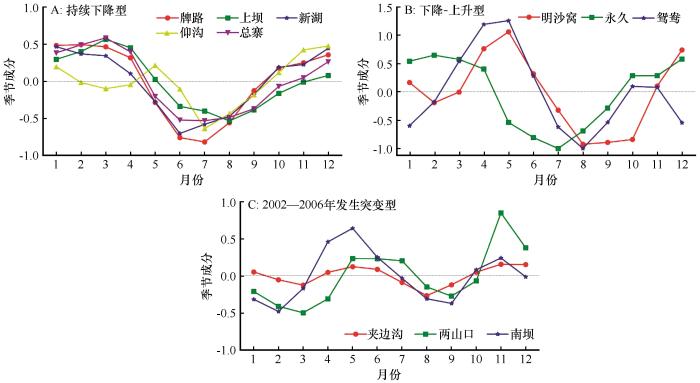
3类地下水观测井均表现出较强的年度季节性，图5显示了3类观测井的月度季节成分在一年内的变化规律。持续下降型观测井SGI的季节成分在5—9月为负值，地下水位较低；在3—6月季节成分呈下降趋势（仰沟为5—7月）；7月至次年3月又逐渐变大，即地下水位开始上升。下降-上升型观测井SGI的季节成分在6月中旬至9月中旬呈现负值，此外，永久观测井在4月中旬至6月中旬、明沙窝观测井在1月中旬至3月和9月中旬至11月、鸳鸯观测井在11—12月的季节成分也呈负值。2002—2006年发生突变型观测井SGI的季节成分在零值附近波动，特别地，在1—3月及8—10月季节成分小于零，显示出地下水位的季节性下降。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 SGI-1的年度季节成分

Fig.5 Annual seasonal component of SGI-1

季节强度是衡量SGI序列季节性波动规律性的指标。观测井的季节强度较高，特别是牌路、上坝、永久的季节强度超过0.7，SGI季节性波动尤为显著，而夹边沟的季节强度较低（0.1873），SGI季节性变化相对平缓（表6）。SGI季节峰值（指一年中地下水位最高的月份）通常出现在冬季的12、2月和春季的3、5月，与农业活动紧密相关。春季（3—5月）气温回暖，土壤解冻，灌溉需求增加，推动SGI上升。夏季（6—8月）高温蒸发量大，许多作物此时生长旺盛，灌溉需求达到高峰，大量抽取地下水导致SGI季节成分普遍为负。秋季（9—10月）作物成熟，灌溉减少，地下水开采量下降，SGI季节成分开始转正。受其他人类活动，如工业用水、生活用水以及地下水位的变化可能存在一定滞后性的影响，个别观测井在非灌溉期SGI的季节成分也呈负值。

4 结论与展望

4.1　结论

地下水是淡水资源的重要组成部分，过度开采地下水导致干旱区绿洲面临严重的地下水干旱问题。本文通过构建标准化地下水指数（SGI）分析了酒泉绿洲地下水干旱的动态变化特征。首先，选用lgN分布、EV分布、GEV分布、Gamma分布、Beta分布和Weibull分布6种概率分布函数构建酒泉绿洲11个地下水观测井的SGI，并基于K-S检验与AIC准则得到结论：Gev分布和Beta分布在长期和短期内均具有较好的拟合优势，且Beta分布的适用性随时间尺度的增加而增强。基于此，本文运用K-Means聚类法将观测井在最优拟合分布下的SGI分为3类：持续下降型、下降-上升型以及2002—2006年发生突变型，并通过STL时间序列分解法揭示了这3类观测井SGI的趋势和季节性变化特征：持续下降型观测井因远离河流和农业灌溉期大量抽取地下水，SGI持续下降，地下水干旱程度由2000年前的非干旱逐步恶化至轻度甚至重度干旱；下降-上升型观测井在1985—2002年因灌溉设施老化而SGI下降，2002年后因水库补给和节水灌溉技术普及而SGI小幅上升，地下水干旱程度不明显；2002—2006年发生突变型观测井在2002年受农业政策影响SGI值下降，2005—2006年因种植结构调整和降水不均再次突变，2006年后随种植结构的稳定SGI值趋于稳定但持续为负，地下水干旱表现为长期持续的中度至重度干旱。此外，受农业灌溉用水增加大量抽取地下水的影响，SGI的季节峰值主要集中在冬季的12、2月和春季的3、5月。

4.2　展望

一方面，SGI的构建对概率分布函数的选择较为敏感，不同的拟合分布函数可能导致截然不同的结果^［12］。未来研究将致力于探索更为优化的方法，减少对特定分布函数的依赖，提高评估精度。另一方面，当前研究主要关注地下水干旱本身，而实际上地下水干旱与传统干旱类型（气象干旱、水文干旱、农业干旱和社会经济干旱）之间相互影响、相互作用^［5］。为了全面理解干旱现象及其驱动因素，未来研究需要将地下水干旱与其他类型干旱相结合。这将有助于深入分析气候变化和人类活动对地下水资源的长期影响，以期为水资源的可持续利用和干旱风险的防范提供更为科学的依据。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Qiu

China faces up to groundwater crisis

［J］.Nature，2010，466（7304）：308.