0 前言
沉积物粒度特征是反映物源和沉积地环境信息——流体动力性质和条件、气候等的敏感性指标[1-2],被广泛应用于风成、海洋、湖泊、河流和浊流沉积环境的比较和沙丘成因分析鉴别[2-8]。沉积物的粒度特征也是影响其输移量的重要参数,为防沙工程设计提供了重要参考。平均粒径(Mz)、分选系数(σ)、偏度(SK)、峰度(Kg)是粒度分析中常用的粒度参数。过去广泛采用的粒度参数计算方法是Trask于1930年提出的。这种方法需要从累积频率分布曲线图上读出特定的累积百分数所对应的粒径[9],耗时耗力并且受人为因素影响较大。目前,计算沉积物粒度参数的方法主要有Folk-Word图解法[10]和矩法[11-13]。Folk-Word图解法的Mz、σ、SK的计算公式形式稳定;针对Kg公式,为了适用于特定系统,德尔和李玉文先后于1970年、1988年进行了改进[14],但公式的实质仍然未变,都着眼于粒度分组区间的某种比例关系。Folk-Word图解法2007年被确定作为中国海洋地质地球物理调查的国家标准[15]。矩法运用数理统计原理定量表征粒度特征[16]。激光衍射(LD)法作为一种新型的粒度测定方法具有样品需求量少(1~3 g)、快速、测量范围广等优势,并且可以大大提高测定效率,从而简化矩法公式的运用[17]。矩法计算公式通用的有两种:McManus矩法[11]和Friedman矩法[13]。两种矩法Mz和σ的计算公式一致,区别在于SK和Kg的计算。Friedman矩法SK和Kg的计算采用传统的统计学方式,分别用离差三次方、四次方对应除以标准差(分选系数)的三次方、四次方。就SK而言,当粒度频率曲线对称分布时,离差三次方后正负离差可以相互抵消,因而SK的分子等于0,则SK=0;当粒度频率分布不对称时,正负离差不能抵消,就形成了正或者负的SK。SK绝对值越大,表示其粒度频率曲线的峰所对应的粒径值偏离平均粒径程度越高。在计算SK时,将离差三次方除以分选系数是为了将SK值转化为相对数,Kg类似[18]。而MaManus矩法SK和Kg的计算分别采用三阶中心矩、四阶中心矩进行消阶,其物理意义尚不清楚[19]。Kg和σ都反映数据的集中趋势,所不同的是,Kg越大,数据越集中,恰恰与σ的数值意义相反。所以,从统计学意义上看,Kg和σ应当负相关,这与前人的研究结论一致[20]。
沉积物的粒度特征主要受物源和沉积环境的影响。虽然风沙流的运移机制以及运移过程中沙粒所产生机械作用是极其复杂的,但沙物质粒度分布特征同沙源物质属性具有直接关系[1]。新疆塔克拉玛干沙漠风成沙粒径以极细沙为主,平均粒径为0.121 mm(3.05 Φ)[21];古尔班通古特沙漠[22]和乌兰布和沙漠[23]优势粒级为细沙和极细沙,平均粒径分别为0.095 mm(3.40 Φ)、0.14 mm(2.83 Φ)。当环境中搬运介质动力过强时,而未达到沉积物粗粒部分所需的动力,细粒物质随动力流流失,表现为亏损状态,粗粒部分就地沉积,粒度频率曲线表现为负偏;而沉积物细粒部分含量高,说明这一环境搬运介质动力不足,粒度频率曲线表现为正偏[24]。所以,偏态多与沉积环境相关。粒度频率曲线上的细尾和粗尾部分对于判断沉积物所处的环境最为关键。据前人研究,风成沙、河流沙多正偏,海岸沙多负偏[24]。
风成沉积物以细颗粒为主,且物源和水动力较单一。本文采集3组风成沉积物样本,共222个,分别用Folk-Word图解法、McManus矩法、Friedman矩法计算平均粒径(Mz)、分选系数(σ)、偏度(SK)、峰度(Kg),比较3种粒度参数计算方法的异同点,为寻找适合风成沉积物粒度参数计算方法提供重要依据。
1 材料与方法
3组样本分别用S55(内蒙古自治区额济纳旗额策S315公路两侧55个)、M98(青海省玛多98个)和R69(四川省若尔盖69个)表示。粒度测试在中国科学院兰州资源环境科学大型仪器区域中心完成。用Mastersizer3000激光粒度仪进行分析,测量范围为0.01~3 500 um,重复测量的相对误差≤0.5%,准确性误差[-1,1]。扫描速度快达10 000次·s-1,可根据需要自行设定。
表1 图解法和矩法粒度参数计算方式
Table 1
2 结果与分析
Folk-ward图解法根据沉积物粒度频率累积曲线上特定的体积百分比所对应的粒径来计算粒度参数,比如Φ5、Φ95分别表示概率累积曲线上从粗粒一端开始累积直到累计体积达到5%、95%时所对应曲线上的粒径值,忽略了小于5%和大于95%部分,误差较大。Folk-ward图解法是在还没有激光粒度仪以及计算机技术不太发展的时期提出的。随着信息技术的发展,矩法由于含有比Folk-ward图解法更加全面的粒度信息而得到广泛的应用。根据已有的资料累积和野外试验,研究者发现沉积物大多为多相体系,因此决定了峰态曲线除有一个明显的主峰外,还存在多个次峰,在此方面矩法比图解法具有优越性。矩法是利用一次矩、二次矩、三次矩、四次矩来分别定义Mz、σ、SK、Kg,所含信息丰富,具有统计学意义。MaManus矩法和Friedman矩法Mz和σ参数的计算方法一致,差别在于SK和Kg参数的计算。根据表1可以看出使用MaManus矩法计算的SK和Kg是有量纲的,与使用Friedman矩法计算的SK和Kg参数存在本质的差异。
3组样品粒度参数统计值均呈现了两个明显的特征(表2):①使用图解法计算的SK均出现了负值。E55样品SK最小值为-0.47,最大值为0.16,平均值-0.19;M98样品最小值为-0.50,最大值为0.10,平均值为-0.29;R69样品最小值为 -0.66,最大值为-0.06,平均值为-0.41。两种矩法计算的SK均无负值出现。②使用Friedman矩法计算的Kg偏大,3组样品使用图解法和McManus矩法计算的Kg相差较小,而其分别与Friedman矩法均相差10以上,最大可达16。所以,针对不同方法计算的粒度参数应建立不同的等级划分,比如就分选性而言,分选中等与分选好的界限因不同的计算方法而异。结合3组样品特征,分析以上差异仅仅是由公式形式导致的,与沉积环境和沙源无关。
表2 3组沉积样粒度参数统计值
Table 2
| 粒度参数 | E55样品组 | M98样品组 | R69样品组 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 最小值 | 最大值 | 平均值 | 标准差 | 最小值 | 最大值 | 平均值 | 标准差 | 最小值 | 最大值 | 平均值 | 标准差 | |||
| Mz1957 | 1.95 | 3.41 | 2.71 | 0.38 | 2.10 | 5.10 | 3.07 | 0.57 | 1.38 | 3.76 | 2.77 | 0.45 | ||
| Mz1982(Mz1988) | 2.07 | 3.66 | 2.91 | 0.43 | 2.11 | 4.95 | 3.22 | 0.53 | 0.62 | 3.82 | 3.02 | 0.40 | ||
| σ1957 | 0.70 | 2.06 | 1.22 | 0.26 | 0.52 | 2.30 | 1.20 | 0.35 | 0.49 | 2.28 | 1.28 | 0.31 | ||
| σ1982(σ1988) | 1.18 | 1.98 | 1.46 | 0.18 | 0.99 | 2.12 | 1.37 | 0.21 | 0.98 | 2.11 | 0.52 | 0.21 | ||
| SK1957 | -0.47 | 0.16 | -0.19 | 0.17 | -0.50 | 0.10 | -0.29 | 0.12 | -0.66 | -0.06 | -0.41 | 0.10 | ||
| SK1982 | 0.73 | 2.74 | 1.89 | 0.48 | 0.52 | 3.66 | 1.89 | 0.58 | 0.98 | 3.71 | 2.16 | 0.53 | ||
| SK1988 | 1.42 | 2.17 | 1.78 | 0.14 | 0.92 | 2.19 | 1.65 | 0.16 | 1.51 | 2.29 | 1.93 | 0.16 | ||
| Kg1957 | 0.92 | 2.87 | 1.89 | 0.65 | 1.00 | 2.66 | 1.65 | 0.35 | 1.02 | 3.28 | 2.29 | 0.51 | ||
| Kg1982 | 3.65 | 12.01 | 7.62 | 1.99 | 2.02 | 18.65 | 7.57 | 3.08 | 2.60 | 19.18 | 7.55 | 3.00 | ||
| Kg1988 | 2.20 | 2.78 | 2.39 | 0.13 | 1.73 | 2.80 | 2.21 | 0.16 | 2.05 | 2.81 | 2.45 | 0.18 | ||
单位为Φ,除SK1957、SK1982、Kg1957、Kg1982外,粒度参数都带有单位。
2.1 不同解析方法对应的平均粒径、分选系数差异
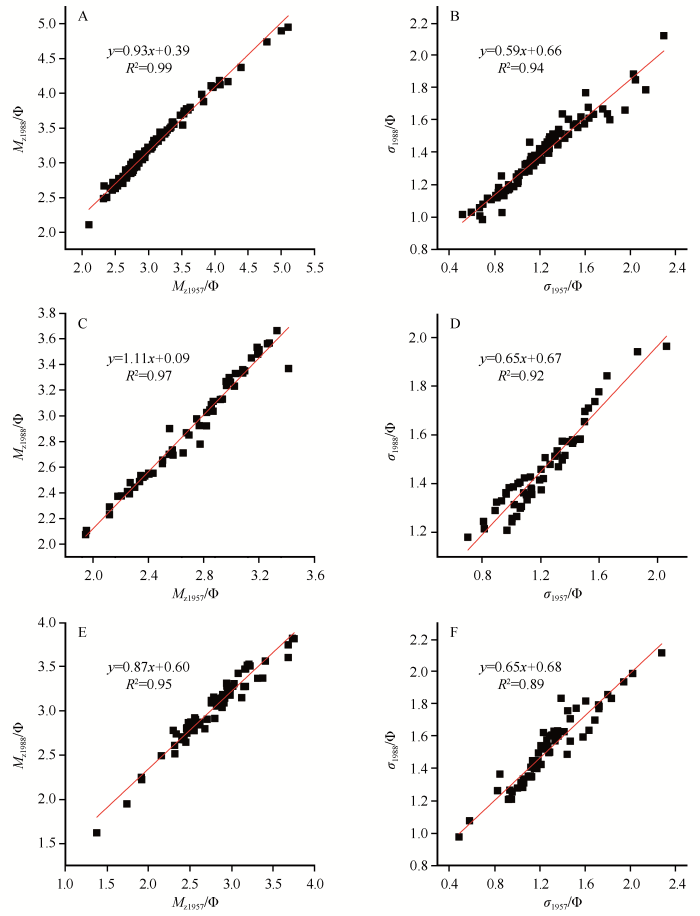
使用图解法和矩法计算的E55、M98和R69组样品Mz和σ具有很强的相关性,相关系数分别为0.99、0.99、0.97和0.98、0.99、0.95,双尾显著检验显示,在0.05的水平下相关性显著。对二者建立回归模型(图1),并进行显著性检验,结果表明6个回归模型均在0.05的水平下,斜率显著不为0。
图1
图1
图解法和矩法计算的平均粒径(Mz)和分选系数(σ)回归分析(A、B:E55;C、D:M98;E、F:R69)
Fig.1
The regression models of Mz and σ for Graphical-Method(abscissa) and Moment-Method(ordinate)
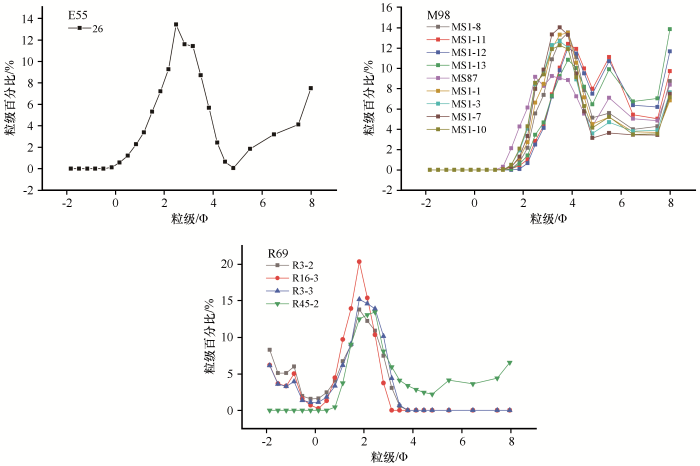
对3组样品Mz、σ之差进行统计分析,用矩法减去图解法。结果表明:208个风成沉积物的Mz和σ都表现出矩法计算结果大于图解法;其余14个风成沉积物中,有8个样本Mz和σ的矩法计算结果小于图解法,6个样本的Mz之差为正、σ之差为负。E55组中编号26的样品Mz和σ之差都为负值;M98组中编号MS1-8、MS1-11、MS1-12、MS1-13、MS87样品Mz和σ之差均为负值,MS1-1、MS1-3、MS1-7、MS1-10中Mz之差为正,σ之差为负;R69组中R3-2、R16-3的Mz和σ之差均为负值,R3-3、R45-2的Mz之差为正,σ之差为负(表3)。图解法较适用于数据分布特征接近正态分布的情况,而当沙物质粒度频率分布曲线为单峰且正偏时,矩法计算结果要大于图解法[13]。E55组26号样品Mz1957为3.41 Φ,Mz1988为3.37 Φ,粒度频率曲线显示其峰值在2.5 Φ左右,因此为正偏(图2)。矩法计算结果却小于图解法,原因是其粒度频率分布曲线右尾的作用。中值粒径为7.9 Φ时,沙物质含量7.49%,超过5%,造成Φ95增大。根据Folk-Word图解法公式可知,Mz和σ也会不同程度地增大。M98组样品Mz1957、Mz1988均在3.97~5.10 Φ,对比频率粒度分布曲线图可知仍然为正偏,部分曲线右尾明显上翘,有次峰;MS1-3、MS1-7、MS1-10样品频率粒度分布曲线次峰微弱,右尾较低,故其Mz差值为正,且均大于0.10 Φ;R69组样品除R45-2有上翘的右尾外,其余3条曲线左尾明显,但其曲线峰所对应的粒径值在2 Φ左右,依旧正偏(图2)。R3-3、R45-2样品两种计算方法之差基本持平,出现了正值。曲线的尾部在粒度分析中至关重要,特别是当曲线多峰时且主峰和次峰不明显时,情况更为复杂。
表3 典型样品粒度参数(Mz、σ)统计值
Table 3
| 样品组 | 编号 | Mz1957 | Mz1988 | σ1957 | σ1988 | Mz1988 - Mz1957 | σ1988 - σ1957 |
|---|---|---|---|---|---|---|---|
| E55 | 26 | 3.41 | 3.37 | 2.06 | 1.96 | -0.05 | -0.10 |
| M98 | MS1-8 | 4.40 | 4.37 | 1.80 | 1.64 | -0.03 | -0.16 |
| MS1-11 | 4.79 | 4.74 | 1.82 | 1.60 | -0.05 | -0.22 | |
| MS1-12 | 5.00 | 4.89 | 1.95 | 1.66 | -0.11 | -0.29 | |
| MS1-13 | 5.10 | 4.95 | 2.14 | 1.78 | -0.16 | -0.35 | |
| MS87 | 4.20 | 4.16 | 2.05 | 1.85 | -0.03 | -0.20 | |
| MS1-1 | 4.07 | 4.18 | 1.60 | 1.57 | -0.04 | -0.09 | |
| MS1-3 | 4.08 | 4.12 | 1.76 | 1.67 | 0.11 | -0.03 | |
| MS1-7 | 3.97 | 4.08 | 1.64 | 1.61 | 0.10 | -0.02 | |
| MS1-10 | 3.97 | 4.09 | 1.68 | 1.63 | 0.12 | -0.04 | |
| R69 | R3-2 | 3.69 | 3.60 | 2.28 | 2.11 | -0.09 | -0.17 |
| R16-3 | 3.38 | 3.37 | 1.83 | 1.83 | -0.01 | -0.004 | |
| R3-3 | 3.13 | 3.15 | 1.94 | 1.93 | 0.02 | -0.01 | |
| R45-2 | 3.32 | 3.37 | 2.02 | 1.98 | 0.05 | -0.04 |
图2
2.2 不同解析方法对应的偏态差异
偏态可作为分布不对称的测度,测度偏态的统计量是偏度(SK)。当SK为正时,表明频率分布曲线的峰相对于正态分布曲线偏左,曲线显示细延的右尾,此时为正偏或细偏;当SK为负时,表明峰偏右,频率分布曲线显示粗延的左尾,此时为负偏或者粗偏;当SK为0时,曲线对称分布。从表2可以看出,使用3种方法计算的SK存在差异,特别是使用Folk-ward图解法公式计算的SK相对于两种矩法来说,明显偏小,3组样品均有负值出现。E55组样品SK1957范围在-0.47~0.16,平均值为-0.19;M98组样品SK1957范围-0.50~0.10,平均值为-0.29;R69组样品SK1957范围-0.66~-0.06,平均值为-0.41。E55组样品SK1982、SK1988范围0.73~2.74、1.42~2.17 Φ,平均值为1.89、1.78 Φ;M98组样品SK1982、SK1988范围0.52~3.66、0.92~2.19 Φ,平均值为1.89、0.65 Φ;R69组样品SK1982、SK1988范围0.98~3.71、1.51~2.29 Φ,平均值为2.16、1.93 Φ;3组样品SK1982范围最大,数据离散度最高。
对3组样品偏态系数两两计算相关系数:E55组样品 SK1957和SK1982、SK1988的相关系数分别是0.35、0.65;M98组样品SK1957和SK1982、SK1988的相关系数分别是-0.45、0.56;R69组样品SK1957和SK1982、SK1988的相关系数分别是-0.86、-0.55。3组样品SK1957和SK1982、SK1988的相关系数均通过了置信水平为0.05的显著性检验。E55、M98、R69组样品两种矩法的相关系数分别为-0.04、-0.09、-0.43,均为负相关,并且只有R69组样品通过了显著性检验。另外还有一点要注意的是,使用MaManus矩法所计算的偏态系数带有量纲,是否可以计算其与其他变量的相关系数以及两者相关系数的意义尚不明确。综上,偏态参数不可互相替代。
2.3 不同解析方法对应的峰态差异
峰态是对数据平峰或者尖峰程度的测定。测定峰态的统计量为峰度(Kg)。Kg反映沉积物主要粒级集中程度。相对于正态分布而言,若沉积物粒度频率分布曲线较为高瘦,则表示主要粒级分布较集中,即在很窄的粒级范围内,曲线包围的面积越大。Kg和σ都反映数据集中程度,但Kg的数值意义与σ相反,Kg越大,粒级分布越高于正态曲线。使用图解法和McManus矩法计算的3组样品Kg相差较小,而与Friedman矩法均相差10以上,最大可达16。E55组样品Kg1957范围0.92~2.87,平均值为1.89;M98组样品Kg1957范围1.00~2.66,平均值为1.65;R69组样品Kg1957范围1.02~3.28,平均值为2.29。E55组样品Kg1982、Kg1988范围分别为3.65~12.01、2.20~2.78 Φ,平均值是7.62、2.39 Φ;M98组样品Kg1982、Kg1988范围分别为2.02~18.65、1.73~2.80 Φ,平均值为7.57、2.21 Φ;R69组样品Kg1982、Kg1988范围分别为2.60~19.18、2.05~2.81 Φ,平均值是7.55、2.45 Φ(表1)。Kg1957和Kg1988数量级相当,Kg1982数值跨度较大。因此,针对不同公式计算的Kg应有不同的定性解释标准。
对使用3种方法计算的Kg两两计算相关系数可知:3组样品Kg1957和Kg1982、Kg1988的相关系数较低且均无通过显著性检验,但两种矩法的相关系数分别为-0.77、-0.41、-0.43,均为负相关并且均通过了置信水平为0.05的显著性检验。
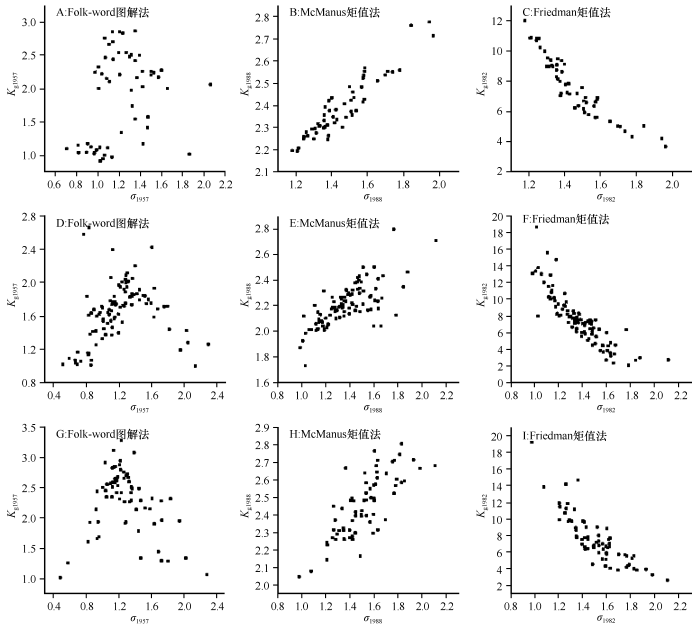
使用Folk-Word图解法计算的3组样品σ、Kg散点图没有呈现任何趋势;McManus矩法均正相关,E55、M98、R69组样品相关系数分别为0.94、0.73、0.78,Kg随σ的增加而增加;Friedman矩法均负相关,E55、M98、R69组样品相关系数分别为-0.93、 -0.87、-0.85,Kg随σ的增加而减小(图3)。由分析可知,Kg与σ的数值意义相反。所以,建议在数据分析时采用Friedman矩法。
图3
图3
σ相对于Kg的散点图(A、B、C:E55;D、E、F:M98;G、H、I:R69)
Fig.3
The scatter diagram of σ and Kg
3 结论
使用图解法和矩法计算的平均粒径和分选系数均呈高度相关性,与沉积环境无关,可互换; 3种计算方法得到的偏度和峰度均不可相互替代,与沉积环境和粒度频率分布曲线的形态关系密切。
当沙物质粒度频率分布曲线为单峰且正偏时,或者为双峰且主峰居左,矩法计算结果一般大于图解法,仍然有少数样品矩法略微小于图解法。对其粒度频率分布曲线分析可知,这些沉积物样品尾部上翘明显:E55组26号样品中值粒径为7.9 Φ时,沙物质含量7.49%,超过5%,造成Φ95增大。根据Folk-Word图解法公式可知,Mz和σ也会不同程度地增大。M98组样品粒级分布除有类似趋势外,其粒度频率分布曲线还有次峰。R69组样品除R45-2有上翘的右尾外,其余3条曲线左尾明显且所在粒级中值粒径对应的含量百分比超过5%;曲线峰值在2 Φ左右,小于Mz,依旧正偏。R3-3、R45-2样品两种计算方法之差基本持平,出现了正值。
沉积物粒度频率分布曲线的形态越简单(平尾、单峰、对称),不同方法计算的粒度参数的差异越小。曲线的尾部在粒度分析中至关重要,特别是当曲线多峰时且主峰和次峰不明显时,情况更为复杂。
从统计学上看,Kg应当与σ的数值意义相反,即二者负相关。所以,在风成沉积物粒度参数的分析中,建议采用Friedman矩法。
参考文献
Grain size characteristics of dune sands in the central Taklimakan Sand Sea
[J].
雅鲁藏布江河谷加查-米林段沙丘成因
[J].
雅鲁藏布江米林宽谷段新月形沙丘粒度分异研究
[J].
腾格里沙漠东南缘格状沙丘粒度特征与成因探讨
[J].
联系沙漠-黄土演变过程中耦合关系的沉积学指标
[J].
Effective grain size distribution analysis for interpretation of tidal-deltaic facies:West Bengal Sundarbans
[J].
Brazos River bar:a study in the significance of grain size parameters
[J].
Grain size determination and interpretation
[M]//Tucker M E.
Machine Processing of Geological Data
[R].
Exercises in Sedimentology
[M].
图解法与矩法沉积物粒度参数的对比
[J].
矩值法和图解法计算山区河流沉积物粒度参数的差异
[J].
南黄海沉积物粒度分布参数计算方法的比较
[J].




 甘公网安备 62010202000688号
甘公网安备 62010202000688号