0 引言
目前干旱半干旱区面积约占全球陆地面积的41%,受全球气候变化的影响,全球大部分地区干旱指数逐年上升,全球干旱面积仍有进一步增大的趋势[1]。水资源匮乏是限制这些区域发展的瓶颈,揭示区域水分循环和耗散的机制是研究干旱区水资源问题的前提和基础。水分循环和水汽耗散(主要指由植物蒸腾、土壤蒸发和冠层截留组成的生态系统蒸散发(ET))是这些地区最重要的生态过程[1-3]。干旱半干旱地区降水量有限,地下水和内陆河是大多数干旱半干旱区水资源的主要来源,尤其在干旱的荒漠区,通常沿内陆河及地下水位较浅的区域分布着荒漠河岸林,形成典型的荒漠绿洲景观,与周围的荒漠环境相比,植物蒸腾作用导致强烈的生态系统ET是主要的区域水汽耗散过程[4]。因此,深入研究荒漠河岸林生态系统ET及其控制机制,对于了解干旱半干旱地区的需水量与耗水量、提升区域水资源管理能力、增强荒漠生态系统稳定性、降低荒漠环境脆弱性具有重要意义[5-7]。干旱半干旱区内陆河多数属于季节性河流,地下水是荒漠河岸林植物最直接和最可靠的水资源[4,8]。由植物引起的地下水蒸散发(ETg)是荒漠河岸林生态系统ET的重要组成部分,准确估计ETg对于进一步研究河岸林生态系统水平衡、揭示荒漠河岸林水分运动机制、合理利用地下水、提供荒漠区水资源管理的新思路和维持区域可持续发展具有重要意义。
目前由于ETg存在时空可变性,估测生态系统ET的方法,在直接量化ETg上存在困难[9]。因此目前估算ETg并不使用ET测量方法,而主要采用水量平衡法、稳定同位素法、极限埋深法和昼夜水位波动法。昼夜水位波动法凭借其所需参数少、费用低和适合长期连续测量的优势成为目前研究ETg最广泛的方法[8-12]。基于昼夜水位估算ETg的方法首先由White[13]提出,随后很多学者对经典White方法进行改进。Hays[14]假设ETg只发生在地下水位下降期间进而估算日尺度ETg;Loheide[15]考虑地下水位波动区域内外连续地下水水流的影响,通过去趋势方法对小时尺度的ETg进行估算;Soylu等[8]基于傅里叶变换对White方法进行改良。考虑植物蒸腾和根系吸水之间存在的时滞效应,在计算日尺度ETg时,White、Hays和Soylu方法比Loheide方法具有更高的精度,被广泛用于荒漠河岸林ETg研究[16]。目前有许多技术可用于估测生态系统ET(涡度相关法、蒸渗仪法和波文比法),其中涡度相关法理论假设少,精度高,从气象学的角度实现对ET非破坏性的长期连续观测,是当前各生态系统应用最广泛的通量和ET监测方法。
本研究以黑河下游额济纳绿洲七道桥荒漠河岸胡杨林(Populus euphratica)为对象,基于数据的完整性和可靠性,选择2014年和2020年6—8月的地下水位数据,应用White、Hays方法和Soylu方法估算胡杨林的ETg,并将估算结果与生态系统ET进行相关性分析,分析ET与ETg差异的原因以及ETg主要影响因子。研究结果有助于进一步理解和认识荒漠河岸林的水分耗散状况,以期为遏制环境恶化、合理管理水资源和恢复绿洲生态提供合理依据。
1 研究区概况
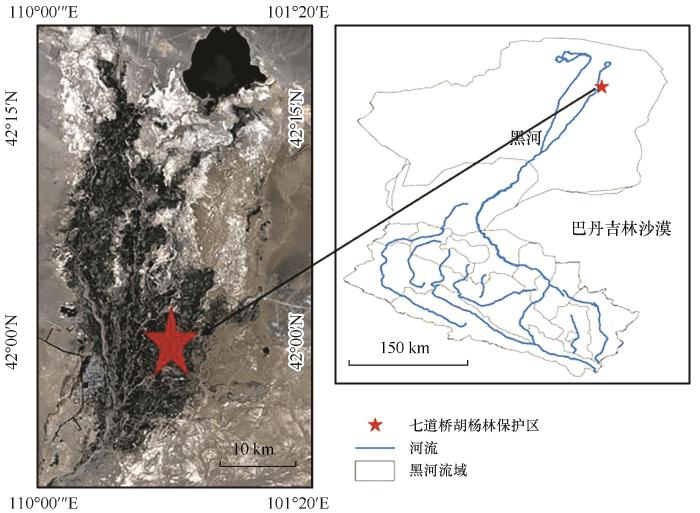
研究区位于黑河下游额济纳绿洲达来呼布镇东南的七道桥胡杨林保护区(41°59′N、101°10′E,海拔921 m,图1),面积1 333 hm2,该区域深居内陆,降水稀少,气候极端干旱,年平均降水量37.9 mm,集中在6—8月;而年平均潜在蒸发量2 225.8 mm(E-601测量水面蒸发),约为年平均降水量的60倍[6];年平均气温为8.9 ℃,7月平均气温最高(27 ℃),1月平均气温最低(-11.7 ℃)。该区域为典型的荒漠河岸林生态系统,主要由胡杨(乔木)、柽柳(灌木)和苦豆子(草本)组成,其中胡杨为研究区的优势建群种,林分特征和土壤质地如表1所列[2]。区域内布设涡度通量观测塔和地下水位监测井来监测涡度通量和地下水位变化。由该区域降水稀少,除每年固定月份(一般为3、9月各1次)的生态输水外,地下水为该区域植被的主要补给水源。
图1
表1 胡杨林分特征和土壤质地
Table 1
| 植被覆盖度 /% | 植株密度 /(株·hm-2) | 树高 /m | 胸径 /cm | 林龄 /a | 土壤质地 | ||
|---|---|---|---|---|---|---|---|
| 0—60 cm | 60—120 cm | 120—150 cm | |||||
| 75 | 350 | 10.1±1.7 | 22.9±4.8 | 30—60 | 沙壤土 | 沙土 | 沙、黏土混合 |
2 数据与方法
2.1 数据观测及预处理
2.1.1 地下水位数据观测及预处理
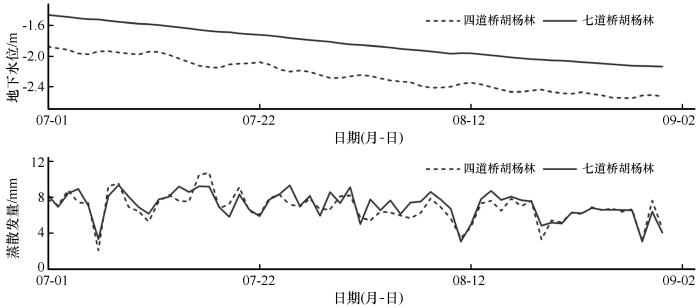
在七道桥胡杨林保护区涡度通量观测塔30 m处布设地下水位观测井,井深6 m,井内安装了HOBO自动水压传感器和水温传感器,同时在井外也安装了HOBO传感器监测外部大气压,每10 min监测1次。根据两个传感器记录的压强之差,获取相应的地下水位。研究区地势平坦,地表植被均一性好,距离主河道较远,且观测井附近无其他抽水井,地下水位变化主要受地表植被和生态输水的影响。考虑胡杨林群落尺度边界效应的影响,其蒸散发存在一定的时空异质性,七道桥一个地下水位观测孔的地下水位数据是否具有代表性存疑,因此将七道桥和四道桥胡杨林(位于七道桥2 km之外,其内也布设地下水位观测井)地下水位和蒸散发变化进行对比(图2),结果表明四道桥和七道桥胡杨林地下水位和蒸散发变化基本一致,说明在胡杨林群落尺度上,地下水位变化趋势是一致的,位于七道桥胡杨林的地下水位观测井数据可代表研究区地下水位变化状况。
图2
图2
2014年四道桥和七道桥胡杨林地下水位和蒸散发同期对照变化
Fig.2
Contrast changes of groundwater depth and evapotranspiration in the Populus euphratica forests in Sidaoqiao and Qidaoqiao in 2014
2.1.2 涡度数据观测及预处理
在研究区架设涡度通量塔观测七道桥胡杨林生态系统地气之间的水汽和能量交换,观测仪器和数据采集仪器如表2[18]所示。对涡度观测得到的原始通量数据,利用Eddypro软件进行异常值剔除、谱分析与校正、双坐标旋转校正、响应频率修正、超声虚温修正和空气密度变化校正,得到0.5 h平均通量数据[19-22];考虑夜间通量数据的可靠性和湍流稳定性,剔除夜间CO2通量为负值和摩擦风速u*<0.16 m·s-1的数据;缺失数据利用R语言的“REddyProc”包进行插补,利用入射短波辐射(Rg)、空气温度(Ta)和饱和水汽压差(VPD)与通量数据之间的关系以及通量数据的时间自相关性进行插补[23]。数据插补后,2014年和2020年能量闭合度均处于合理范围[24],可以基于波文比能量平衡对LE进行校正[12,25]。
表2 涡度观测数据及仪器
Table 2
| 仪器 | 名 称 | 观测及采集对象 | 采样间隔及频率 |
|---|---|---|---|
| 观测仪器 | 三维超声风速仪(CSAT3, Campbell Co, 美国) | 风速 | — |
| 开路式CO2/H2O分析仪(Li-7500A, LI-COR, 美国) | 水汽和CO2浓度 | ||
| 四分净辐射仪(CNR4, Kipp & Zonen, 荷兰) | 净辐射(Rn) | ||
| 相对温湿度传感器( HMP45C, Campbell,美国) | 气温(Ta)、湿度(RH) | ||
| 土壤热通量板( HFP, Hukse Flux Thermal Sensors B.V. , Delft, 荷兰。埋设在地下5 cm处,水平间隔0.5 m) | 土壤热通量(G) | ||
| 数据采集仪器 | CR3000数据采集器 | 通量观测数据、净辐射(Rn)、气温(Ta)、相对湿度(RH) | 采样间隔:30 min 采样频率:10 Hz |
2.2 数据处理与方法
2.2.1 地下水蒸散发
2.2.1.1 地下水蒸散发计算
研究区内生态系统ET有可能来自于4个水源:灌溉水、降水、土壤水、地下水。因此基于水量平衡,地下水蒸散发ETg可定义为:
2.2.1.2 地下水蒸散发计算方法
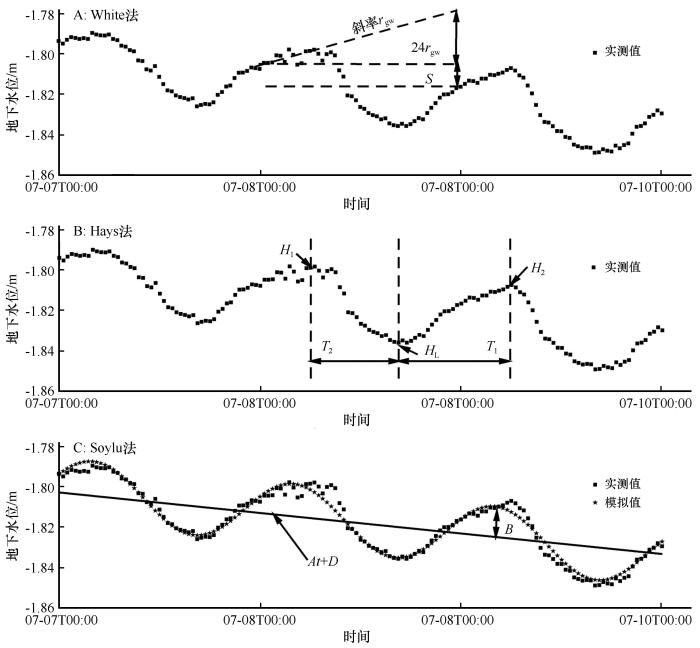
式中:ETg代表日尺度的地下水蒸散发(mm);Sy代表给水度;rgw代表地下水位恢复速率(mm·h-1);S代表24 h内地下水位的净上升或下降。Sy的取值主要与土壤质地有关,Loheide等[27]提出计算Sy的有效方法,根据研究区地下水所处深度的土壤质地数据,Sy的取值最终为0.08。rgw的取值由夜间水位恢复曲线拟合得到。White方法假设夜间ET为0,地下水恢复速率在1 d内是恒定的(大多数自然生态系统不满足这一假设)[1],用夜间地下水位恢复速率代表全天的地下水位恢复速率。原始的White方法rgw采用00:00—04:00的地下水恢复速率,本文在后文选择不同的时间窗口对rgw进行拟合,验证了使用00:00—04:00拟合地下水恢复速率是合理的。
图3
Hays方法。Hays[14]提出了一种采用灵活的时间周期计算ETg的方法,公式如下:
式中:H1是当天地下水位峰值(mm);H2是次日地下水位峰值(mm);HL是当天地下水位谷值(mm),T1是地下水位从当天谷值回升到次日峰值所需的时间(h),T2是地下水位从当天峰值下降到谷值所需要的时间(h)。该方法与White方法类似,但仅考虑H1和HL之间的蒸散发,并将其作为1 d的蒸散发。
Soylu方法。地下水位变化具有周期性和正弦性,Soylu等[8]将地下水位数据与时间序列进行经验拟合,提出如下公式:
式中:Z(t)代表t时刻的地下水位(mm);A代表水位变化趋势斜率(mm·h-1);D代表截距;B代表昼夜振幅(mm);E代表昼夜相位(h)
对地下水位进行去趋势后,得到地下水位日变化幅度2B,但实际去趋势处理会移除一部分ETg信号,削弱地下水位随时间序列上升和下降的幅度,因此将每日ETg简单地等同于Sy(2B)会低估每日ETg,需要引入比例因子k来进行校正[8],公式如下:
式中:k代表比例因子,k的大小取决于蒸腾曲线的形状和持续时间,主要与太阳辐射有关,使用每小时入射太阳辐射数据表示ETg曲线的日形状,对1 d内的太阳辐射数据进行迭代累积,然后对时间序列进行去趋势化,得到1 d的比例因子k[8]。
2.2.2 蒸散发计算
基于波文比能量平衡,强制能量闭合,对利用涡度系统得到的半小时尺度的LE数据进行校正,进而利用LE数据得到研究区生态系统半小时尺度的ET(mm)数据,计算公式如下[28]:
式中:ET代表生态系统半小时尺度的蒸散发量(若计算结果小于0,则用0表示);LE代表半小时尺度的潜热通量(MJ·m-2);L代表水的汽化潜热(2.45 MJ·kg-1);ρw代表水的密度。
2.2.3 相关性计算
Pearson相关系数是统计学上重要的三大相关系数之一,适用于分析两个存在线性关系且服从正态分布的连续变量之间的相关性程度。其取值范围为-1—1,当Pearson相关系数为0—1时,变量存在正相关性,当Pearson相关系数为-1—0时,变量之间存在负相关性,绝对值越大,相关性越强[29]。
目前还没有研究去定量该研究区地下水和土壤水对研究区ET的贡献,因此并不清楚该区域地下水蒸散发的实测值,无法利用其他评价模型精度的指标来评价模型好坏,但研究内降水稀少,远离河道,研究期内也无其他抽水灌溉事件发生,地下水位变化与研究区生态系统ET密切相关,ETg和ET之间存在较为一致的变化趋势,所以通过对胡杨林ETg(3种算法)和ET进行Pearson相关性检验,分析3种算法的计算精度。
3 结果与分析
荒漠河岸林生态系统蒸散中,植物蒸腾占据主导地位,由于降水稀少,地下水是植物蒸腾作用的主要水源,因此地下水蒸散发(ETg)在生态系统蒸散(ET)中占据很大比重,ETg与生态系统ET密切相关,将在很大程度上反映生态系统ET的变化。
3.1 地下水日动态变化
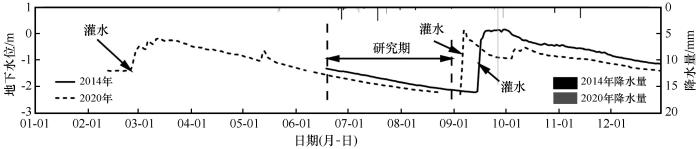
研究区分别在3月和9月发生灌水事件,灌水之后地下水位迅速上升,甚至地面出现积水,之后地下水位缓慢下降(图4);由于降雨事件发生较少,地下水位的变化未因其产生明显的波动。昼夜水位波动法适用于无降水、灌溉和抽水事件发生的时段,因2014年9月15日发生灌溉事件和2020年9月5日分别发生灌溉事件,且2014年只有6月19日至12月31日的地下水位监测数据,因此分别选取两年中6月19日至8月31日作为研究期,研究ETg日动态变化,该时间段内地下水位波动下降,除了仅有的几次微弱降雨事件发生,无灌溉和抽水事件发生。
图4
图4
2014年和2020年胡杨林地下水位日动态变化
Fig.4
Daily dynamic changes of Populus euphratica forest groundwater depth in 2014 and 2020
3.2 日尺度 ETg
3.2.1 White方法的最优时间窗口选取
图5
图5
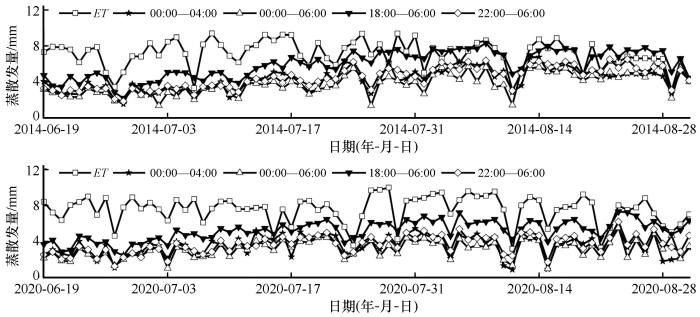
2014年和2020年采用White方法基于不同时间窗口估算的ETg与生态系统ET
Fig.5
ETg estimated based on White′s method in different time windows and ecosystem ET in 2014 and 2020
数据符合正态性检验,不同时间窗口估算的ETg与生态系统ET之间的Pearson相关系数(表3):00:00—04:00>18:00—06:00>22:00—06:00>00:00—06:00,因此采用White方法估算该区域ETg时,选择00:00—04:00计算地下水补给率最为合理。
表3 2014年和2020年采用White方法基于不同时间窗口估算的 ETg 与生态系统 ET 之间的Pearson相关性分析
Table 3
| 年份 | 00:00—04:00 | 00:00—06:00 | 18:00—06:00 | 22:00—06:00 |
|---|---|---|---|---|
| 2014 | 0.33** | 0.29* | 0.30** | 0.27** |
| 2020 | 0.45** | 0.37** | 0.40** | 0.43* |
*代表P<0.05,相关性显著;**代表P<0.01,相关性极显著。
3.2.2 Soylu方法的最佳移动窗口选取
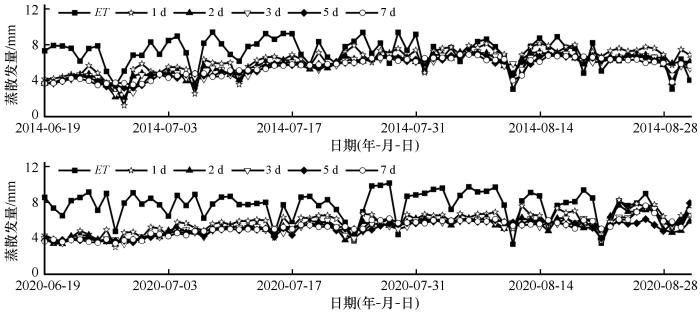
从Soylu方法计算ETg时采用1—7 d的移动窗口对地下水位动态变化进行24 h的拟合,移动窗口的选择对曲线的拟合具有一定的影响,时间窗口不同,昼夜振幅B不同,B的变化会直接影响ETg的计算,选择不同的时间窗口(1、2、3、5、7 d)对地下水变化曲线进行拟合,分别计算ETg(图6,k=1.9),并将计算结果与生态系统ET进行相关性分析。
图6
图6
2014年和2020年采用Soylu方法基于不同移动窗口估算的ETg与生态系统ET
Fig.6
ETg estimated based on Soylu method in different moving windows and ecosystem ET in 2014 and 2020
数据符合正态性检验,不同移动窗口估算的ETg与生态系统ET之间的Pearson相关系数(表4):1 d>2 d>3 d>5 d(7 d),因此采用Soylu法估算该区域ETg时,选择1 d的移动窗口最为合理。
表4 2014年和2020年基于Soylu方法不同移动窗口估算的 ETg 与生态系统 ET 之间的Pearson相关性分析
Table 4
| 年份 | 1 d | 2 d | 3 d | 5 d | 7 d |
|---|---|---|---|---|---|
| 2014 | 0.43** | 0.31** | 0.25* | 0.21 | 0.19 |
| 2020 | 0.41** | 0.29* | 0.21 | 0.19 | 0.15 |
*代表P<0.05,相关性显著;**代表P<0.01,相关性极显著。
3.2.3 日尺度 ETg 与生态系统 ET
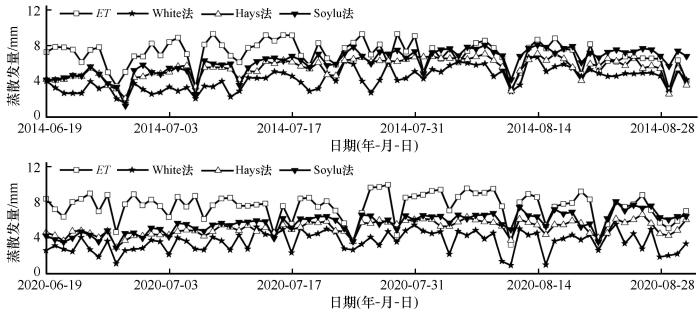
如图7所示,分别用White、Hays法和Soylu方法估算2014年和2020年胡杨林生长季旺盛期的ETg,并与同期生态系统ET进行比较,结果表明,采用3种方法模拟的ETg与生态系统ET的日变化趋势一致,但6月中旬至7月上旬ETg与生态系统ET差异明显,表明这一时期不仅地下水供应生态系统ET,土壤水等也参与生态系统ET过程;7月下旬至8月下旬,除White方法计算的ETg与生态系统ET有明显差异,其他两种方法计算结果与生态系统ET差异较小,表明这一时期主要由地下水供应生态系统ET。
图7
图7
2014年和2020年生长旺盛期胡杨林生态系统蒸散(ET)和地下水蒸散发(ETg)
Fig.7
Ecosystem evapotranspiration (ET) and groundwater evapotranspiration (ETg) of Populus euphratica forest during the peak of the growing season in 2014 and 2020
数据符合正态性检验,不同方法估算的逐日ETg与生态系统ET之间的Pearson相关性(表5):Hays>Soylu>White,Hays方法计算结果最好,其次是Soylu方法,White方法最差,因此选择Hays方法计算ETg是最合理的。
表5 2014年和2020年基于White、Hays法和Soylu法估算的 ETg 与生态系统 ET 之间的Pearson相关性分析
Table 5
| 年份 | White法 | Hays法 | Soylu法 |
|---|---|---|---|
| 2014 | 0.33** | 0.64** | 0.43** |
| 2020 | 0.45** | 0.59** | 0.41* |
*代表P<0.05,相关性显著;**代表P<0.01,相关性极显著。
3.3 日尺度 ETg 影响因素
图8
图8
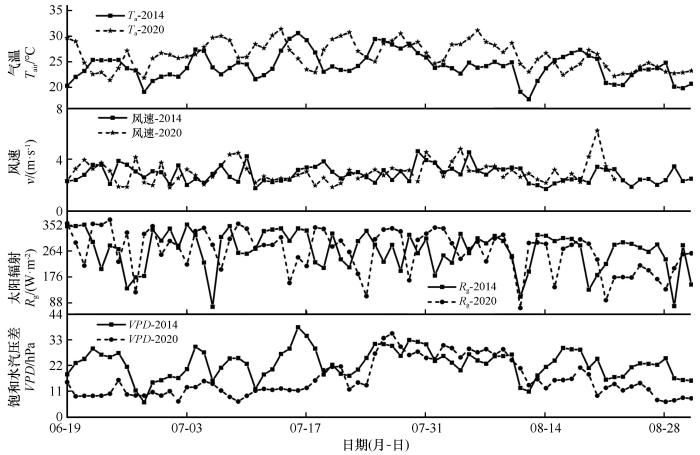
2014年和2020年生长旺盛期胡杨林生态系统气象因子变化
Fig.8
Variations of meteorological factors in Populus euphratica forest ecosystem during the peak growth season in 2014 and 2020
表6 2014年和2020年 ETg 与地下水位、气温、风速、太阳辐射和 VPD 之间的Pearson相关性
Table 6
| 年份 | 地下水位/m | 气温/℃ | 风速/(m·s-1) | 入射太阳辐射/(W·m-2) | VPD/hPa |
|---|---|---|---|---|---|
| 2014 | -0.41** | 0.47** | 0.02 | 0.50** | 0.60** |
| 2020 | -0.54** | 0.19* | 0.04 | 0.36** | 0.54** |
*代表P<0.05,相关性显著;**代表P<0.01,相关性极显著。
ETg(根据3.2Pearson相关性分析结果,ETg为Hays方法计算结果)与温度、太阳辐射和VPD存在显著的正相关关系(P<0.01),其中与VPD的相关性在所有影响因素里绝对值最大,相关性最强(2014:0.60, 2020:0.19);与地下水位之间呈显著的负相关关系(P<0.01);与风速无相关性(P>0.05),表明风速与ETg过程无关。
根据Pearson相关性分析结果,以地下水位、气温、太阳辐射和VPD为自变量,ETg为因变量,在R语言中进行多元逐步线性回归,对数据进行线性假设检验、正态性检验、同方差性检验、独立性检验、多重共线性检验(气温与VPD具有共线性)和异常值检验,由于气温和VPD具有共线性,因此以地下水位、太阳辐射和VPD为自变量,ETg为因变量,建立多元线性模型(多元线性回归假设检验通过),模型结果如表7所示。
表7 2014年和2020年地下水位、太阳辐射和 VPD 与 ETg 线性模型系数及 R2
Table 7
| 年份 | 自变量 | 代表符号 | 系数 | R2 | 调整后R2 | 模型P值 |
|---|---|---|---|---|---|---|
| 2014 | 地下水位/m | X1 | -2.276** | 0.685 | 0.672 | <0.01 |
| 太阳辐射/℃ | X2 | 0.008** | ||||
| 饱和水汽压差VPD/hPa | X3 | 0.081** | ||||
| 常量 | — | -2.388** | ||||
| 2020 | 地下水位/m | X1 | -2.609** | 0.706 | 0.693 | <0.01 |
| 太阳辐射/℃ | X2 | 0.006** | ||||
| 饱和水汽压差VPD/hPa | X3 | 0.021** | ||||
| 常量 | — | -2.118** |
*代表P<0.05,相关性显著;**代表P<0.01,相关性极显著。
根据表7中显示的结果,建立多元线性回归模型:
2014年:Y=-2.276X1+0.008X2+0.081X3-2.388,调整后R2=0.672,P<0.01,说明ETg变化的67.2%可以由地下水位、太阳辐射和VPD的变化来解释。
2020年:Y=-2.609X1+0.006X2+0.021X3-2.118,调整后R2=0.693,P<0.01,说明ETg变化的69.3%可以由地下水位、太阳辐射和VPD的变化来解释。
计算结果表明,地下水位、太阳辐射和VPD等能很好地解释ETg的变化过程,除地下水位、太阳辐射和VPD外,ETg变化过程还受其他因子的影响。
3.4 地下水对生态系统 ET 贡献率
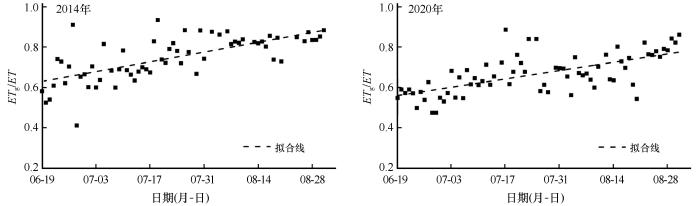
如图9所示,2014年和2020年6月19日至8月31日研究期间,地下水对生态系统ET的贡献率呈随时间上升的趋势,从6月中旬的56%左右上升至8月末期的80%左右,表明随着生长季的进行,土壤含水量减少,地下水成为维持生态系统ET的主要来源,植物利用更多的地下水用于蒸腾作用,因而地下水对生态系统ET的贡献率不断增大。随生长旺盛期日益深化,ET水平也随之加剧,大大增加土壤水分受胁迫的程度,因此地下水在一定程度上对土壤水进行上移补给。
图9
图9
地下水对生态系统蒸散发(ET)贡献率
Fig.9
Contribution rate of groundwater to ecosystem evapotranspiration
4 讨论
4.1 地下水位波动法合理性
2014年和2020年胡杨林ETg研究期间地下水位一直呈波动下降趋势,使用White、Hays方法和Soylu方法模拟的ETg日变化趋势与生态系统ET基本一致,且具有显著的相关性关系,仅在降雨事件发生时模拟ETg与生态系统ET相关性较差,因此使用地下水位波动法模拟ETg是合理的。3种方法中White方法精度最低,与人为主观选取计算地下水恢复速率时段有关,且实际夜间ET并不为0,导致White方法估算的ETg与实际相比被低估[30]。Hays方法根据地下水位波动曲线将地下水分为补给和耗散两个阶段,并不人为选取ETg为0的时段,人为因素导致的误差小,是3种方法中精度最高的方法[10]。Souly方法基于Fourier对White方法改进,且该方法不考虑地下水补给速率,但计算中使用的比例因子k使得计算过程较其他两种方法更为复杂,目前在中国ETg研究中应用较少。
4.2 日尺度 ETg 影响因子
本研究表明胡杨林ETg与地下水位存在显著的负相关关系,即随地下水位的增加ETg增加,该结果与Yu等[6]对黑河下游七道桥胡杨林和孙海涛等[31]对塔里木河流域的胡杨林和柽柳林的研究结果一致,但与Yue等[9]研究结果相反。Yue等[9]研究结果表明ETg与地下水位呈显著的正相关关系,存在差异的原因可能与植被类型有关,Yue等[9]研究区植物为草本科植物,根系分布较浅,随地下水位增加,植物可吸收利用地下水减少,由植物蒸腾导致的ETg也随之减少,所以随地下水位增加ETg减少。而胡杨属于深根系植物,其根系发达,地下水位在一定阈值范围内不会造成对胡杨的水分胁迫,因此虽然研究区6—8月干旱程度增强,地下水位持续下降,胡杨仍会吸收利用更多的地下水。
4.3 生态系统 ET 与 ETg 差异性
胡杨林ETg研究期间,基于昼夜水位波动法估算的每日ETg与生态系统ET变化趋势基本相同,但二者在研究期间尤其是6、7月存在较大差异,造成差异的主要原因是生态系统ET不仅来自于土壤水还来自于地下水,研究区5—8月土壤含水量一直处于下降趋势,尹力等[26]也发现七道桥胡杨主要吸收利用40—60 cm土壤水和地下水(地下水位超过1.5 m),因此可以说明生态系统ET有一部分来自于土壤水蒸散发,这是ET和ETg存在差异的主要原因。同时随着生长季的推移生态ET与ETg之间的差异逐步缩小,说明随着生长季的进行,植物可利用土壤水含量减少,转而更多地利用地下水,同时随着干旱程度的增强,地下水对上层土壤的补给作用也增强,因此ETg占ET的比例逐步增大。
5 结论
本文基于涡度数据对七道桥胡杨林生态系统的能量分配和生态系统ET进行研究,基于昼夜水位波动法对胡杨林ETg进行了估算。
基于昼夜水位波动法估算日尺度ETg是合理的,White、Hays和Soylu 3种方法计算结果均与生态系统ET存在良好的相关性,Hays方法计算结果最优,模拟精度最高。
地下水位、太阳辐射、气温、VPD与ETg存在显著的相关性,由此建立的多元线性混合模型可以解释ETg 68%左右的变化。
生长季随着干旱程度增加,地下水对生态系统ET的贡献率逐步增大。
参考文献
Expansion of global drylands under a warming climate
[J].
Comparison and modification of methods for estimating evapotranspiration using diurnal groundwater level fluctuations in arid and semiarid regions
[J].
How changes of groundwater level affect the desert riparian forest ecosystem in the Ejina Oasis,Northwest China
[J].
Energy fluxes and evapotranspiration over irrigated maize field in an arid area with shallow groundwater
[J].
Evapotranspiration of a Populus euphratica Oliv.forest and its controlling factors in the lower Heihe River Basin,Northwest China
[J].
Impact of agricultural water-saving practices on regional evapotranspiration:the role of groundwater in sustainable agriculture in arid and semi-arid areas
[J].
On evapotranspiration and shallow groundwater fluctuations:a Fourier-based improvement to the White method
[J].
Spatiotemporal patterns of water table fluctuations and evapotranspiration induced by riparian vegetation in a semiarid area
[J].
Estimation of groundwater evaportranspiration using diurnal water table fluctuations in the Mu Us Desert,northern China
[J].
Application of the water table fluctuation method for estimating evapotranspiration at two phreatophyte-dominated sites under hyper-arid environments
[J].
Water use by saltcedar (Tamarix sp
.) and associated vegetation on the Canadian,Colorado and Pecos Rivers in Texas[D].
A method for estimating subdaily evapotranspiration of shallow groundwater using diurnal water table fluctuations
[J].
黑河流域边界数据集
(
An Introduction to environmental biophysics
[J].
Calculating CO2 and H2O eddy covariance fluxes from an enclosed gas analyzer using an instantaneous mixing ratio
[J].
Post-field data quality control
[M]//Beverly L,Shashi V.
Quality Control and Flux Sampling Problems for Tower and Aircraft Data
[J].
A comparison of eddy-covariance and large aperture scintillometer measurements with respect to the energy balance closure problem
[J].
Energy balance closure at FLUXNET sites
[J].
Basic and extensible post-processing of eddy covariance flux data with REddyProc
[J].
On the consequences of the energy imbalance for calculating surface conductance to water vapour
[J].
Estimation of groundwater consumption by phreatophytes using diurnal water table fluctuations:a saturated-unsaturated flow assessment
[J].
Estimating groundwater evapotranspiration by a subtropical pine plantation using diurnal water table fluctuations:implications from night-time water use
[J].
Response to environmental flows in the lower Tarim River,Xinjiang,China:ground water
[J].
Estimation of evapotranspiration using diurnal groundwater level fluctuations:comparison of different approaches with groundwater lysimeter data
[J].




 甘公网安备 62010202000688号
甘公网安备 62010202000688号