随着中国“一带一路”倡议不断推进，西部地区的区位劣势逐步得以改善，大面积的荒漠、戈壁丰富的太阳能、风能资源，赋予了新能源产业发展的地理优势^［1］。2022年国家发展改革委和国家能源局联合发布《以沙漠、戈壁、荒漠地区为重点的大型风电光伏基地规划布局方案》^［2］，以推进“沙戈荒”大型能源基地项目建设，配套建设的变电站、设备间、配电间及办公、居住用房等低矮建筑物的结构安全是保障系统安全稳定运行的基本前提。联合国防灾署的统计资料表明中国是世界上自然灾害造成经济损失最严重的3个国家之一，风灾因发生频率高且影响范围广而成为防灾减灾工作的重点对象^［3］。沙尘暴是干旱、半干旱地区特有的灾害性天气，典型特征为突发性、局地性、持续时间较短而破坏力极强，会造成人畜死亡、毁坏农田农用温室、破坏近地区域（沙尘浓度最大）的房屋及市政基础设施^［4］。由于低矮建筑较低，处于风速变化大、湍流度高、风环境最复杂的大气边界层底部；同时，低矮建筑的几何外形各异，表面气动力作用复杂，对风荷载十分敏感，是极端风环境中最易遭受破坏的一类工程结构^［5］。因此，风工程研究者们围绕低矮建筑在季候风常规大气边界层风场^［6］、台风^［7］、龙卷风^［8］以及下击暴流^［9］等条件下的流场及风荷载特性开展了大量研究，对低矮建筑结构的风致响应有了深入认识。沙尘暴的风场特性受大气热力层结稳定度、强对流、沙粒运动等多重因素影响，风场特性发生显著变化，进而改变结构表面的气动力特征，但还鲜有对沙尘暴环境中低矮建筑的风压特性的系统研究。

Huang等^［10-12］在沙漠地区建立了风沙现场监测平台，得到沙漠典型下垫面的风场特性，进而在边界层风洞中建立模拟沙尘暴的风沙流场，采用测力天平实验研究了风沙作用下低矮建筑模型的整体受力特征，但受测试技术的限制，未得到模型表面的风压分布信息。随着可用计算资源的飞速增长和流体模拟方法的不断发展，计算流体动力学（Computational Fluid Dynamics，CFD）被广泛应用于结构风工程领域研究^［13］。沙尘暴本质上是风沙气-固两相流，从CFD模拟角度来看，两种不同的策略通常被用于求解此类两相流动问题。一种是欧拉-欧拉（Eulerian-Eulerian， E-E）方法，将流体和颗粒均视为连续相，用体积分数描述每一相的存在，求解时两相相互渗透。张默^［14］、白江涛^［15］即采用E-E方法分别对CAARC （Commonwealth Advisory Aeronautical Research Council）标准高层建筑、圆柱工程结构的风场和风沙两相流场进行数值模拟，得到净风和挟沙风作用下结构表面的平均风压分布。E-E方法对小颗粒运动描述相对准确，而对跟随性较差的大颗粒运动描述准确性欠佳，因此不利于准确刻画风沙环境中工程结构的真实受力状态。另一种是欧拉-拉格朗日（Eulerian-Lagrangian， E-L）方法，使用Navier-Stokes （N-S）方程求解连续相运动，将固体颗粒注入流动中，随后跟踪颗粒运动以计算流场中的颗粒轨迹^［16］。陈峥等^［17］采用E-L方法模拟戈壁风沙流，计算了不同风速工况下建筑表面的沙粒冲击压分布以及沙荷载。E-L可提供更全面的粒子、流体相互作用信息，但需要更强大的计算资源^［18］，因此计算时需要将颗粒注入量减少到必要的最低限度^［19］。

以上研究工作均考虑了风沙环境中沙粒的冲击对工程结构整体荷载的增大效应，为风沙地区建筑结构的主体荷载设计提供了参考。然而，均未对挟沙风场中工程结构的风压分布开展精细研究，尤其是对强风沙环境中易造成围护结构及其连接构件破坏的脉动风效应缺乏关注。相比主体结构破坏，风灾中建筑的屋面、侧墙、保温层等围护结构的局部破坏更为常见。鉴于此，本文采用E-L两相流数值方法开展沙尘暴环境中低矮建筑风压特性的数值研究。本研究的目的是探明沙尘暴环境中沙粒运动对风场特性的影响，进一步得到挟沙风场中低矮建筑的风压分布规律，为风沙地区低矮建筑的抗风设计提供参考。由于真实大气边界层尺度的风沙气固两相流数值计算资源消耗十分巨大，因此基于小尺度模型开展风沙问题的研究较为普遍^［20-21］，为获得更精细的分析结果，本文的研究工作也基于小尺度模型开展。

采用三维不可压N-S方程求解流场，引入拉格朗日粒子追踪法求解颗粒运动，考虑流场与运动颗粒之间的相互作用^［22］，则笛卡尔坐标系下加入沙粒对风场反作用力的连续性方程和动量方程可表示为：

式中：u_i 表示i方向的速度；p、ρ=1.225 kg·m^-3和ν=1.5×10^-5 m²·s^-1分别是空气的压力、密度和运动黏度。不考虑温度对风场和颗粒运动的影响，故忽略能量方程。

将沙粒等效成球形颗粒，沙粒在风场中受到拖曳力的同时，也对风场施加大小相等、方向相反的力S_i，S_i 以源项的形式添加到式（2）中，以实现固体颗粒相和流体连续相的双向耦合，S_i 的表达式为：

式中：V_cell为有限控制体体积；n_pcell为控制体中的颗粒总数；A_P为颗粒的迎风投影面积； u 、 u_p分别为流场和颗粒的合速度。

沙粒运动受多种力共同影响，本研究中仅考虑量级最大的重力和拖曳力^［23］；同时计算的风沙流为稀相的气固两相流^［24］，故忽略沙粒间的相互碰撞。沙粒运动符合牛顿第二定律，运动方程表示为：

式中：m_p为沙粒质量；ρp=2 650 kg·m^-3为沙粒密度；重力加速度g=9.81 m·s^-2；d_p为沙粒直径。沙粒所受重力与浮力之和为Fg+Fb=16π(ρp-ρ)dp3g。C_dp为颗粒拖曳力系数^［25］；Re_p为颗粒雷诺数，表达式分别为：

基于Liu等^［26］在甘肃青土湖地区对沙尘暴期间总悬浮沙颗粒的监测结果，近地0.9~30 m高度沙粒的平均粒径为70~105 µm，随着高度的增加平均粒径减小，由于本文的研究对象为低矮建筑，故沙粒粒径取近地区域平均粒径的最大值，粒径均值和标准差分别设置为105 µm和30 µm，且服从对数正态分布^［27］。现场实测沙尘暴期间的总悬浮沙粒质量浓度为10^-7~10^-1 kg·m^-3，低矮建筑高度范围内的质量浓度在10^-4~10^-3 kg·m^-3，故计算质量浓度设置为1.0 g·m^-3。

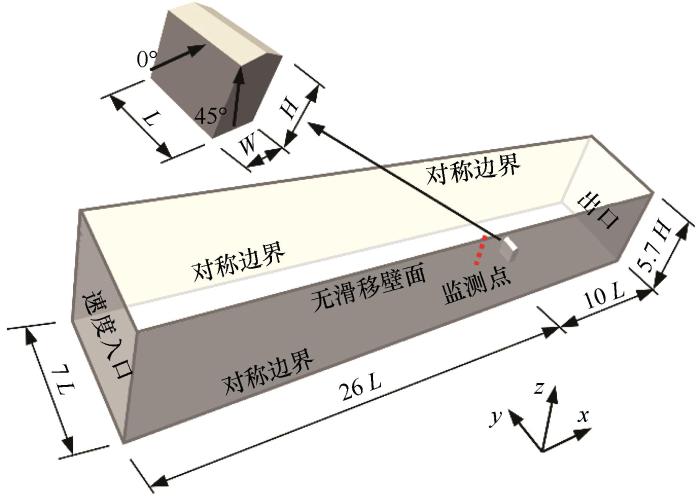
如图1所示，本文研究对象为一屋面坡度15°的双坡低矮建筑模型，几何缩尺比1∶10，长（L）×宽（W）×高（H）为0.5 m×0.3 m×0.44 m，考虑0°（正风向）、45°（斜风向）两个典型风向工况。计算域长×宽×高为36L（x）×7L（y）×5.7H（z），两个风向角下的阻塞率均小于3.0%，满足CFD计算对建筑绕流研究的阻塞率要求^［28］。模型放置在距离入口26L处，经过该距离沙粒与风场的相互作用，在气流的驱动下于模型位置处形成沿宽度方向均匀分布的风沙流场。

计算域为人工合成湍流速度入口（Velocity inlet），采用Melaku等^［29］提出的DFSRTurb湍流生成方法，生成满足目标风场特性的脉动风速时程，出口为自由出流（Outflow），两侧及顶部为对称边界（Symmetry），计算域底部及模型表面采用无滑移壁面（No-slip wall），通过基于速度修正壁面涡黏系数的nut U Rough Wall Function壁面函数^［30］设置壁面粗糙度。沙粒从计算域入口以指示风速（2L高度处的平均风速）水平释放，无滑移壁面的颗粒边界条件设置为反弹，其余边界颗粒均逃逸。

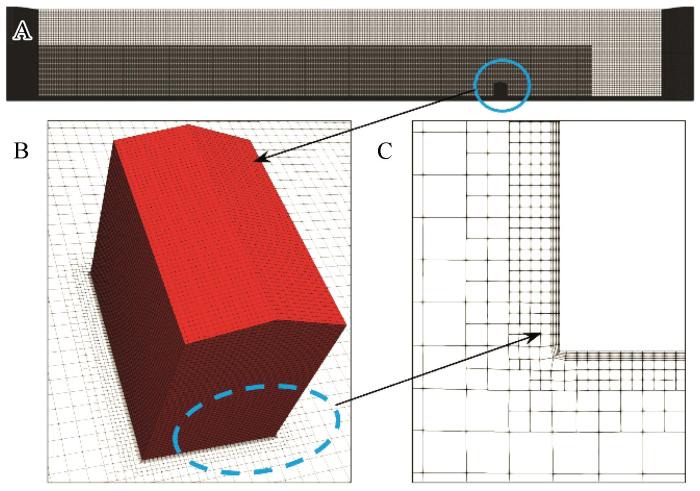
为保证入口湍流特性在计算域内具有良好的自保持性，入口至目标区域之间采用相同的网格分辨率，近壁面区域网格局部加密，壁面第一层网格高度约为0.0014 m （y⁺>25），满足壁面函数计算对第一层网格高度的要求^［31］，边界层网格伸展率1.05。0°和45°风向角模型的网格总数分别为306.9万和305.4万，0°风向角模型计算域及局部网格划分如图2所示，45°模型的网格划分策略与0°模型相同。根据作者前期对该模型网格收敛性的研究^［32］，创建了不同精细程度的3套网格方案——稀疏网格（172万）、基础网格（307万）及加密网格（610万），分别从空气动力学和输沙率角度评估网格分辨率对数值结果的影响。结果显示：基础网格与加密网格的风压结果相对误差在3%以内，本文采用的网格分辨率风压计算结果已达到收敛。

湍流模型采用改进延迟分离涡（Improved Delayed Detached-Eddy Simulation，IDDES）方法^［33］，是一种将雷诺平均（Reynolds Averaged Navier-Stokes， RANS）和大涡模拟（Large Eddy Simulation， LES）相结合的混合方案，在近壁面使用RANS求解小尺度湍流运动，在远离壁面以大涡输运为主要特征的流动分离区域，采用LES对大尺度湍流结构进行解析，以保证空间湍流运动的模拟精度，该方法兼顾了数值计算的效率和求解精度。

采用二阶隐式Backward格式进行时间项离散，对流项、梯度项离散采用二阶精度的高斯线性格式（Second-Order Linear Scheme），扩散项离散使用修正的高斯线性方法（Gauss Linear Scheme），压力与速度耦合采用PISO（Pressure-Implicit with Splitting of Operators）算法，风场非稳态计算时间步长设置为0.001 s，数值计算总时长为23 s，统计后20 s的计算结果。数值计算采用拉格朗日点粒子法求解沙粒运动，通过与文献［12］中低矮建筑在风沙作用下的荷载风洞实验结果对比，验证了本文的数值方法^［32］。

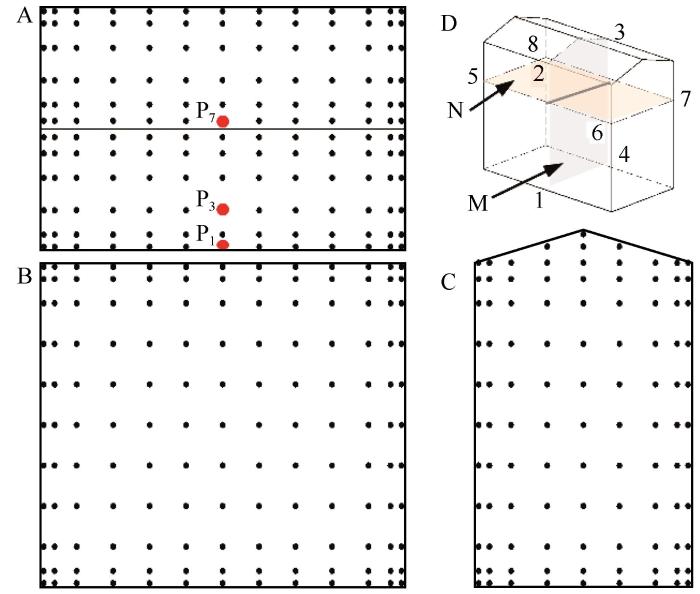
模型表面测点布置如图3，共布置648个测点以提取表面的风压时程数据。在风压变化显著的边缘区域测点布置相对密集，各表面中部区域测点相对稀疏。定义建筑中轴对称面为M截面（1-2-3-4），0.6L高度处的横截面为N截面（5-6-7-8）。

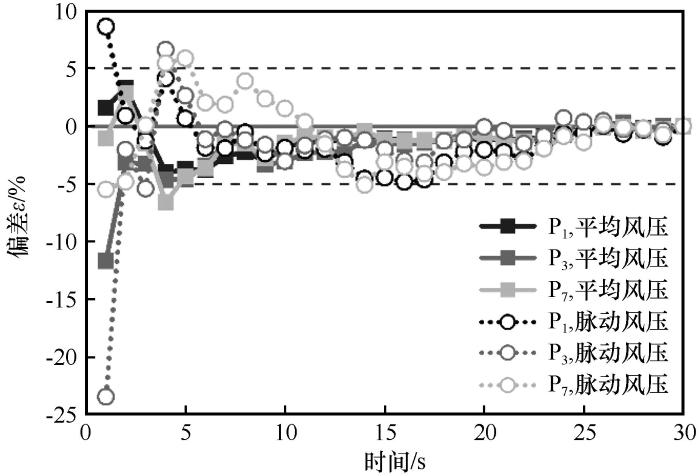
采样时长是影响非稳态湍流模拟统计结果的重要参数^［33］，为保证结果的可靠性，考察了不同采样时长（1~30 s）对风压统计结果的影响。提取12.65 I工况下（工况定义详见2.1节） M截面屋顶（2-3）上P₁、P₃、P₇测点不同统计时长的风压结果，以30 s的结果为参照，不同统计时长下风压平均值与脉动值相对于30 s风压结果的偏差ε定义为：

式中：p_T 、p₃₀分别为采样时长T s和30 s的风压统计结果，包括平均值和脉动值。

图4为P₁、P₃和P₇测点T s的平均风压、脉动风压相对30 s统计结果的偏差ε。可以看出随着采样时间的增加，风压的统计值逐渐趋于稳定，统计时长超过15 s以后，平均和脉动风压的ε都在5%以内。因此，本文数值计算统计时间确定为20 s可以保证结果的可靠性。

风压系数。风压系数为气流在建筑表面引起的压力与来流未扰动风速压力的比值，本文采用檐口高度0.8L作为归一化高度，风压系数定义如下^［34］：

式中：p（t）和C_p （t）为风压及风压系数；p₀为参考静压；U_H为檐口高度处的平均风速（时间平均）；N为风压时程步数；C_p，mean、C_p，rms、C_p，peak分别为平均、脉动、极值风压系数；p^为风压时程中的最大或最小风压值。符号约定：风压使作用表面受压力为正、受吸力为负，本文凡涉及负风压值的大小均为其绝对值的对比。

风压相关系数。相关系数ρXY用于描述两个变量的线性相关程度，脉动风压的空间相关性分析对计算风荷载作用下的共振响应十分重要，任意两点X、Y的压力时程相关系数定义为：

式中：Cov（C_p，X，C_p，Y ）、D（C_p，X ）、D（C_p，Y ）分别代表随机变量测点X与Y风压系数C_p，X 、C_p，Y 的协方差和方差。

风压偏度、峰度。建筑屋面、侧面和背风面等风压受建筑本身引起的非定常流 （Building Induced Turbulence） 影响显著的区域，准定常假定不再成立，风压时程以风压分布的不对称并伴有大幅值的风压脉冲（极值风压）为特点，脉动风压具有显著的非高斯特性，往往是导致围护结构及构件局部破坏的主要原因^［35］。风压系数的偏度和峰度能反映风压时程的偏斜程度和凸起程度，可以作为风压非高斯特性的判定依据，偏度C_Sk与峰度C_Ku表达式分别为：

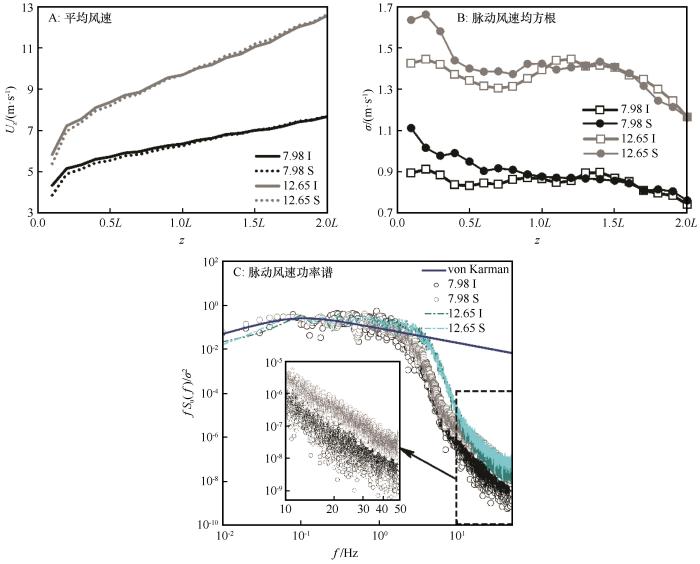
本文计算了两种风速工况——指示风速（净风状态下2L高度处的平均风速）分别为7.98 m·s^-1、12.65 m·s^-1，定义7.98 I代表7.98 m·s^-1风速工况下净风场中的计算结果、7.98 S代表挟沙风场中的计算结果，同理可定义12.65 I和12.65 S。

风场风速及沙粒质量浓度的监测位置均位于模型前方2L处（图1）。湍流风场根据文献［10］中沙漠地区现场实测的风场特性建立，净风场特性与现场实测结果吻合良好^［32］。两种风速工况下，檐口高度0.8L处的沙粒平均质量浓度监测值分别为：7.98 S工况1.097 g·m^-3，12.65 S工况1.052 g·m^-3。

图5A中的平均风速廓线显示挟沙风场中的风廓线相比净风场风速有一定程度的减小，且高度越低风速减小越显著，因为在重力作用下，流场中下部的沙粒浓度相对更大，对风速削弱也更显著。由于流场中沙粒的质量浓度较低（约1.0 g·m^-3），因此风速减小并不明显，此处仅给出4种工况下0.8L高度处的风速值。7.98 I：6.14 m·s^-1；7.98 S：6.00 m·s^-1；12.65 I：9.21 m·s^-1；12.65 S：9.16 m·s^-1。

图5B中的顺风向脉动风速显示，在0~1L高度挟沙风场的脉动风速均方根明显大于净风场中同一高度的脉动风速均方根，说明在低空沙粒浓度较高的区域，颗粒运动增强了气流的脉动强度，并且高度越低脉动增强越显著，而1L以上风场的脉动并没有显著变化。已有大量的现场实测^{［26，36］}及风洞实验^{［10，37-38］}研究显示，流场中颗粒的存在会增强湍流脉动。根据Balachandar等^［39］对颗粒-湍流调制机制的解释，这或许是由于气流与颗粒运动存在速度差，使颗粒形成尾涡脱落而产生新的涡动，并对流场的速度波动造成干扰，从而导致湍流脉动增强。小颗粒对气流的跟随性较好，而大颗粒对气流的跟随性较差，因此粗沙粒对气流的干扰比细沙粒更显著。在沙尘暴环境中，不同高度的沙粒粒径相对集中，随着离地高度的增加沙粒粒径减小，因此沙颗粒对气流的干扰随高度的增加而减弱，这将进一步强化流场脉动上小下大的变化特征。

图5C为檐口高度处顺风向脉动风速功率谱，在低频段（<10 Hz），挟沙风场与净风场的功率谱曲线并没有显著差别，而高频段（>10 Hz），两种风速工况的挟沙风场功率谱值都有一定程度的增大，说明湍流脉动增加是由于沙粒运动增大了流场中小尺度涡的能量，使流场中的高频脉动成分增加，这与Wang等^［36］在沙尘暴现场观测中得出的含沙流动中的小尺度运动能量增强比大尺度结构的能量增强更为明显的结论是定性一致的。脉动风速功率谱在低频段与von Karman谱基本吻合，在高频部分由于LES存在不可避免的数值耗散问题，功率谱值相对较小^［40］。

本文给出7.98 m·s^-1风速工况下0°风向角（正风向）和12.65 m·s^-1风速工况下45°风向角（斜风向）模型的风压统计结果。

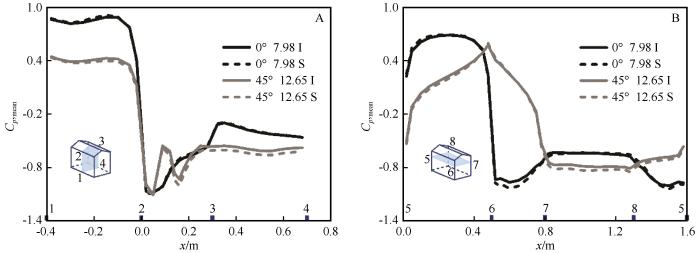
由图6~7可知，挟沙风场中的平均和脉动风压系数与净风场中结果整体趋势一致。图6A的M截面（1-2-3-4）上最大平均负压出现在屋面（2-3）迎风前缘的气流分离处；同时，由于分离涡作用，图7A迎风屋面中部的脉动风压系数达到最大，气流在屋面（2-3）屋脊处发生二次分离，因此在背风屋面的迎风前缘脉动风压也出现一个峰值。图6B中N截面（5-6-7-8）上的最大平均负压：对于0°风向角工况，出现在两侧面（6-7和5-8）迎风前缘部分，该处的柱状涡脱落强烈，图7B中的脉动风压系数也达到最大；45°风向角工况脉动风压系数的最大值出现在6处，由于此处发生了气流分离。

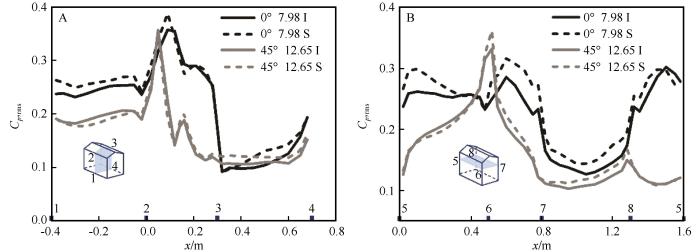
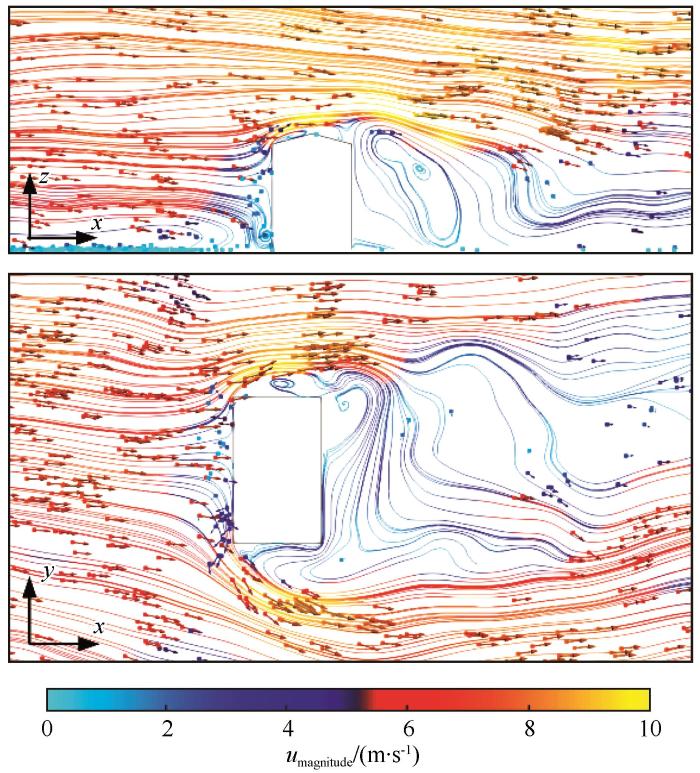
图6挟沙风场的平均风压系数与净风场并没有显著区别，平均风压受湍流脉动影响较小，而挟沙风场中湍流脉动的增强，使图7中的脉动风压系数明显大于净风场中结果。一方面，由于迎风区域的脉动风压受来流自身湍流脉动特性影响显著，基本符合准定常假定，沙粒运动增强流场脉动，使作用在结构迎风区域的脉动风压也显著增大；另一方面，由图8中0°风向角模型立面和水平面上的瞬时流场速度和颗粒运动速度可知，在模型附近区域，由于障碍物的阻挡使气流产生减速和加速绕流，相比远离模型的区域，沙粒在模型附近与气流形成了更明显的速度差，而对气流产生更显著的干扰。同时，沙粒与壁面碰撞后反弹也会进一步增强对气流的扰动。而背风屋面、侧墙面和背风区域则受分离流、尾流等引起的旋涡运动控制，挟沙风场中湍流脉动的增强使这些区域的脉动风压也有一定程度的增大。

在沙尘暴环境中，近地范围内的沙粒浓度较大，沙粒运动增强湍流脉动的同时，使作用在结构表面的脉动风压增大，而脉动荷载是造成结构振动及疲劳破坏的主要原因，因此在风沙地区建造的低矮建筑物、太阳能光伏板等高度较低的建（构）筑物，应更加关注结构的疲劳损伤问题。

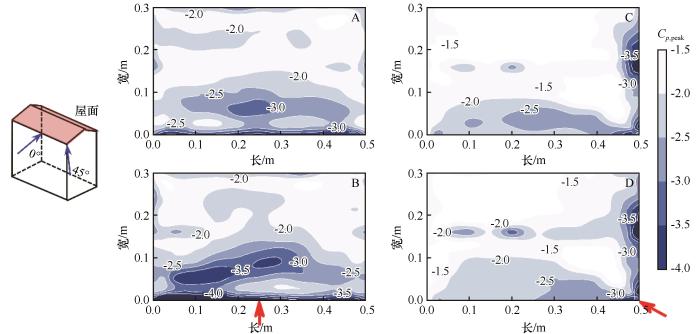
极值风压系数是确定围护结构设计风荷载的重要依据。屋面结构在大风中局部被卷起而损坏的根本原因就是由于负压极值在屋盖表面产生的瞬时强大吸力，因此本文对屋面负压极值的分布特征进行详细对比。

如图9A、B，0°风向角下，屋面的极值风压系数分布较对称，但由于流场中沙粒运动使气流变得更加不稳定，挟沙风场中极值风压系数分布的对称性比净风环境差。由于脉动能量的衰减，极值风压系数沿来流方向梯度减小，图9A净风场中极值风压系数从屋盖前缘区域约-3.0减小至下游约-2.0，最大值为-4.03；图9B挟沙风场中系数由屋盖前缘区域约-4.0减小至-2.0，最大值为-6.02，屋面全部测点极值风压的平均值由净风场中的-2.19增大到挟沙风场中的-2.41，整体增大9.93%，极值风压系数的最大值增大49.22%。

如图9C、D，45°风向角下，来流在屋面前缘角部分离沿屋面两侧形成锥形涡，较高的负压主要分布在屋面角部和与角部紧邻的屋面边缘区域，且越靠近迎风角部负压越大。同样由于能量的衰减，极值风压系数沿流向逐渐减小，系数从屋面角部区域约-3.5减小至屋面下游约-1.5，屋面所有测点的极值风压平均值由净风场中的-1.92增大到挟沙场中的-2.04，整体增大6.25%，净风场和挟沙风场中极值风压系数最大值分别为-5.19和-5.72，最大值增大了10.2%。

由图9可知，挟沙风场中屋面的极值负压总体分布特征相比净风场中结果并没有显著变化，屋面角部、边缘区域的局部极值风压比其余区域值要大得多，依然是风灾中最容易发生破坏的区域^［41-42］。由于挟沙风场中湍流度增大，气流的不稳定性增强，使分离流更早再附于建筑屋面、分离区内的极值风压也更大，因此沙尘暴环境中的建筑围护结构安全受到更严重的威胁。

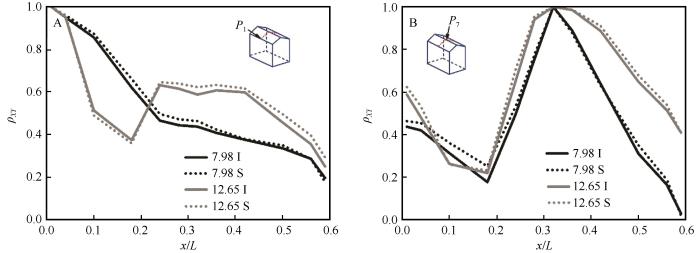
对屋面纵向测点（M截面上2-3）进行风压相关性分析，图10给出了屋面测点间的风压系数相关性曲线，横坐标为测点间的水平位置。图10A和10B分别为屋面迎风前缘测点P₁和屋脊附近测点P₇与屋面上其余测点的风压系数相关性。净风场和挟沙风场中测点间的风压相关性系数总体上具有相同趋势，而挟沙风场中的风压相关性与净风场结果相比有增大趋势，即屋盖局部发生大幅值吸力脉冲并带动周边点形成联动效应的概率增大，这增大了围护结构破坏的风险。

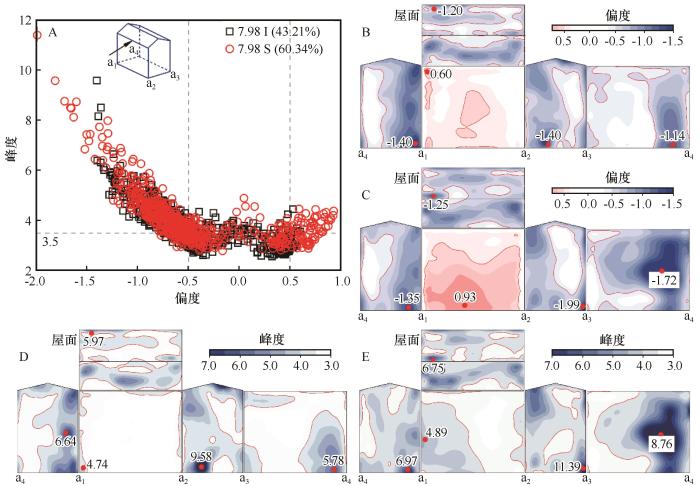
本文采用Kumar等^［43-44］针对低矮房屋风压高斯和非高斯特性设定的判定标准：偏度|C_Sk|>0.5且峰度C_Ku>3.5的测点判定为风压非高斯特性测点。

图11A给出了7.98 m·s^-1来流0°风向角模型测点风压的偏度与峰度统计结果，呈现非高斯特性的测点数百分比挟沙风场为60.34%，净风场为43.21%，测点数增加了39.6%。图11B~E中的红线为偏度|C_Sk|>0.5、峰度C_Ku>3.5的界限区域，风压非高斯特性区域显著增大，统计测点对应的非高斯区域覆盖面积，挟沙风场相对于净风场结果增大了54.8%。从图11B~E各表面的偏度、峰度云图可以看出，除个别测点外，挟沙风场比净风场各个表面的偏度、峰度最值的绝对值均显著增大。图11B、C偏度结果对比表明：正偏最大值由0.60增大到0.93，负偏最小值由-1.40减小到-1.99；图11D、E峰度结果对比表明：峰度最大值由9.58增大到11.39。由此可知，挟沙风场中的风压非高斯特性更加显著。

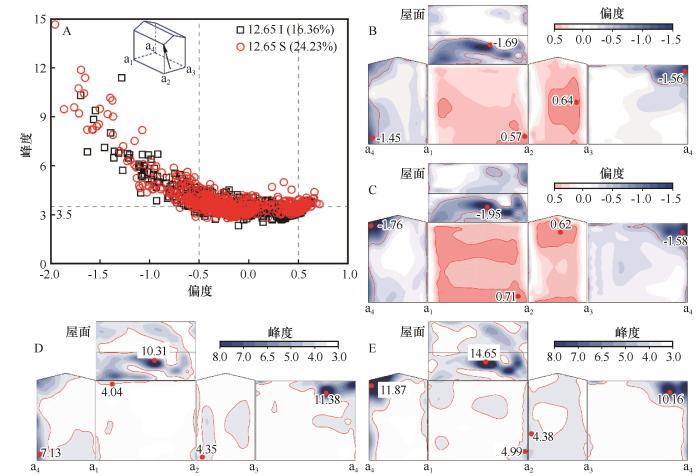
图12A给出了12.65 m·s^-1来流45°风向角模型测点风压的偏度与峰度统计结果，呈现非高斯特性的测点数百分比挟沙风场为24.23%，净风场为16.36%，比例增大了48.1%，图12B~E中红线标定的非高斯特性区域同样显著增大，统计测点对应的非高斯区域覆盖面积，挟沙风场结果增大了52.4%。从图12B~E各表面的偏度、峰度云图可以看出，除个别测点外，挟沙风场相比净风场中各个表面的偏度、峰度最值的绝对值都显著增大。图12B、C偏度结果对比表明：正偏最大值由0.64增大到0.71，负偏最小值由-1.69减小到-1.95；图12D、E峰度结果对比表明：峰度最大值由11.38增大14.65，同样挟沙风场中风压的非高斯特性显著增强。

对净风场和挟沙风场中风压的非高斯特性进行差异性分析。表1中0°、45°风向角模型的偏度和峰度差异性分析结果显示，挟沙风场和净风场中的C_Sk和C_Ku数值差异极显著（P<0.01），证明了挟沙风场中的风压非高斯特性显著增强。

从图11~12偏度、峰度的最值分布区域来看，风压非高斯特性较强的区域主要出现在建筑物边缘、屋脊及柱状涡、锥形涡和尾流作用区域，也是极值负压较大的区域，风压的非高斯区域受风向角影响显著。净风场和挟沙风场中风压非高斯特性区域分布的整体特征没有显著变化，但两种风向角工况下挟沙风场中非高斯特性区域均增大50%以上，即挟沙风场中有更多区域的围护结构容易发生局部撕裂破坏。

沙尘暴环境下，风场中沙粒的存在减小了低矮建筑的风场平均风速，增大了脉动风速，湍流脉动增强是因为小尺度的脉动成分增多，即流场中沙粒运动使小尺度涡的能量增加。

与净风场中低矮建筑的表面风压相比，挟沙风场中的平均风压系数无明显变化，脉动风压系数显著增大。因此在风沙地区建造的高度较低的建（构）筑物，对由脉动荷载导致的结构振动和疲劳损伤问题应更加关注。

挟沙风场中由于风速脉动增大，气流不稳定性增强。与净风场结果相比，屋面的极值风压系数增大6%~10%，屋面测点间的风压相关性系数也有增大趋势。即屋盖局部发生大幅值吸力并带动周边点形成联动效应的概率增大，对建筑围护结构安全造成更大威胁。

净风场和挟沙风场中建筑表面非高斯特性区域的整体分布特征无显著变化，但挟沙风场中风压的偏度、峰度绝对值显著增大，风压非高斯特性更加显著，非高斯特征区域面积增大。因此沙尘暴环境中有更多区域的围护结构面临遭受局部撕裂破坏的威胁。