0 引言
在风沙地貌学研究内容中,沙丘相对高度作为重要形态参数为沙丘形成演化研究提供依据。对于沙丘相对高度的研究至少可以分为以下两类:①沙丘相对高度用于研究沙丘形成演化机理。早在1998年就有学者在塔里木沙漠石油公路沿线监测了沙丘移动,发现沙丘各几何形态参数间存在着较好的相关性,据此总结了沙丘移动规律[1];随着现代遥感技术的不断进步,有学者开始利用30 m ASTER全球数字高程模型(GDEM),分析纳米布沙漠中沙丘的相对高度、间距和等效沙厚等一系列形态指标之间的关系[2]。也有学者利用无人机对荷兰特塞尔岛海岸天然灌丛沙丘进行了监测,得到沙丘的最大高度、体积、面积、植被特征等相关数据,探讨了不同因素对沙丘规模发育的贡献[3]。近年来,有学者在塔克拉玛干沙漠腹地提取了新月形沙丘的15个形态参数和移动速度,分析了沙丘移动速度与形态参数间的相关性,其中沙丘相对高度对移动速度的影响较大[4];有学者通过野外实地测量和高分辨率遥感影像分析,探讨了民勤绿洲外围上风向边缘区域内新月形沙丘形态参数间的沙丘相对高度与宽度比值及沙丘高度与移动速率的关系[5]。②将沙丘相对高度作为研究对象,寻找现存最高大的沙丘,探讨其成因及沙丘相对高度生长的极限。有学者对纳米布沙漠的沙丘相对高度进行了研究,绘制了沙丘相对高度等值线地图[6]。巴丹吉林沙漠被认为有全球最高大的沙丘[7-10]。1990年,学者们利用航片与地形图,提取分析了巴丹吉林沙漠腹地沙丘的长度、宽度、最高点、最低点等参数的变化特征,认为沙丘形态指标符合一般风成地貌规则的分布规律,所以下伏地形不是巴丹吉林沙漠高大沙山形成的主要原因[11];进入21世纪,有学者通过对巴丹吉林沙漠高大沙山的考察以及沙丘形态(沙丘相对高度等)、风况等的研究,探究了巴丹吉林沙漠高大沙山形成发育[12];有学者将沙丘相对高度划分出了4个等级并绘制了沙丘相对高度的等值线地图[13];也有学者研究了巴丹吉林沙漠综合型反向沙丘的高度-间距关系,认为巴丹吉林高大沙山发育过程相对于其他沙漠和水下地形里的叠置沙丘和沙丘而言没有特殊成因[8,13]。但是,有学者也提出了巴丹吉林沙漠高大沙山是多种因素共同作用的结果[9]。此外,随着技术手段的发展,汪克奇等[14]基于数字高程模型,使用数字地形分析算法提取了巴丹吉林沙漠沙丘的相对高度,为沙丘相对高度数据获取提供了新的思路。另外,有学者就沙丘相对高度生长是否存在极大值也展开了探究,结果未发现大气边界层高度限制沙丘大小的证据,相反表明沙丘原则上可能无限地生长,但其生长取决于形态,随着尺寸的增加而放缓,最终可能受到沙量供应的限制[15]。诸多学者围绕沙丘相对高度做出了很多重要的研究,但沙丘相对高度的测量始终是一个难题。
传统的沙丘相对高度测量以人工测量为主,为沙丘地貌研究提供了高精度的基础数据,但受测量条件的约束,难以开展大区域的实地测量[16-18]。随着遥感技术的不断发展,卫星影像被广泛应用于沙丘形态学研究中,也使得沙丘相对高度研究逐渐向大范围方向发展。众多学者均使用了沙丘相对高度=背风坡长度×休止角的正切值这一算法利用遥感影像测量沙丘相对高度[19-23],但沙丘休止角使用统计值,可能与实际情况不符。基于DEM数字高程模型的数字地形分析为沙丘相对高度测量研究带来了历史性的进步,沙丘相对高度算法也逐渐开始完善。有学者为横向沙丘和星状沙丘分别设计了算法,利用沙丘顶点构建不规则三角网,结合风向数据获取目标底点,得到了巴丹吉林沙漠所有独立沙丘的位置和高度,为沙丘相对高度数据获取提供了新的思路[14]。尽管这种方法有效提高了沙丘相对高度计算的准确性和效率,但是算法一方面需要风向等其他数据参与,限制了算法的推广,另一方面需要人工参与划分沙丘类型,给算法引入了人为因素的主观干扰,此外,该算法仅可用于横向沙丘和星状沙丘,并未覆盖所有沙丘类型。基于遥感影像和数字地形模型进行数字地形分析是沙丘形态指标测量的发展趋势,沙丘相对高度测量已经从单个沙丘人工测量发展为遥感大范围自动测量,只是目前测量算法仍有完善的空间。
在设计沙丘相对高度测量算法时,沙丘顶点和底点的选取至关重要。沙丘相对高度是沙丘顶点与沙丘底点的高度差值,沙丘顶点的选取鲜有争议,但沙丘底点选取却各有不同(表1)[2,14,22,24-27]。沙漠边缘或戈壁底部相对平坦,因此即便所选沙丘底点有所不同,但其对沙丘的相对高度测量的影响不大;而沙漠腹地起伏不平,选择不同的沙丘底点对沙丘相对高度测量的影响不可忽略。传统方法测量沙丘相对高度的过程中,沙丘底点是测量人员主观选取的一个地形局部最低值点;而利用数字地形分析方法测量沙丘相对高度时,首先需要设计一个指标描述不同地形局部最低值点之间的差异,然后利用这个指标定量选取最优的局部最低值点。不同的沙丘底点到沙丘顶点的水平距离不同,计算得到的沙丘相对高度也不同,能够在较短水平距离内获得较高的沙丘相对高度,则代表一个沙丘底点对沙丘相对高度的贡献效率较高。本研究给出一个定量的贡献效率定义,并试图基于贡献效率给出沙丘底点的大范围自动选取方法,实现大范围、客观、全自动的沙丘相对高度测量,为沙丘相对高度测量提供新的思路。
表1 沙丘相对高度的定义
Table 1
1 研究方法和数据
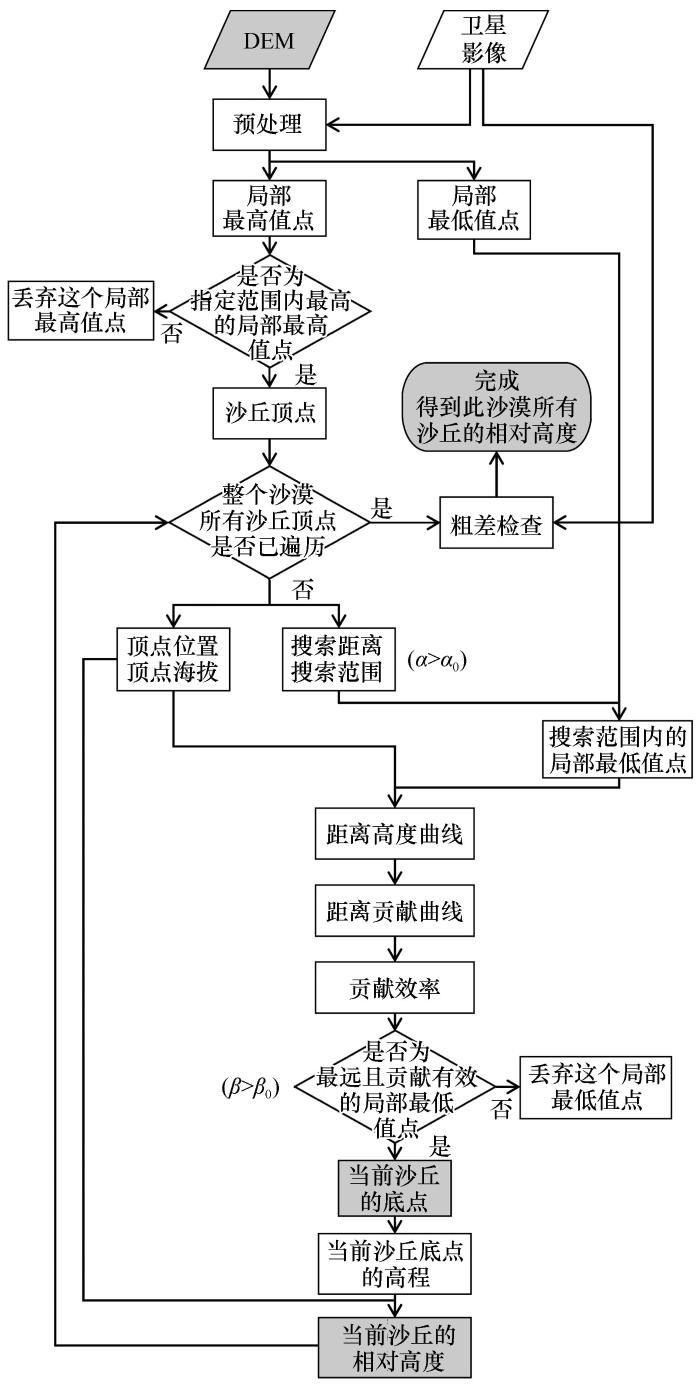
沙丘底点选取是沙丘相对高度测量的关键。本算法以DEM数字高程模型为基础,为每个沙丘计算出各自的搜索距离,在搜索距离内,按照到沙丘顶点的距离远近,将所有局部最低值点进行排序,计算每个局部最低值点的贡献效率,选取贡献有效的最远的一个局部最低值点作为沙丘底点(图1)。
图1
图1
算法流程
Fig.1
Flow chart of the calculation of relative dune heights in a desert
1.1 底点选取原则
沙丘底点是众多地形局部最低值点中的一个,不能距离沙丘太远(即本算法所称“搜索距离”,定义见后文),到沙丘顶点的距离和沙丘大小有关。从沙丘顶点出发,随距离增加,各局部最低值点对沙丘相对高度的贡献效率通常会逐渐减小。沙丘底点应该是搜索距离内贡献有效的最远局部最低值点。
1.2 底点选取方法
DEM预处理:在ArcGIS 10.8软件中结合高分辨率遥感影像和DEM数字高程模型解译出沙漠边界并将沙漠边界内的石质山地等影响沙丘相对高度计算的区域剔除。
沙丘顶点:预处理后的DEM数字高程模型上局部最高值点都是潜在的沙丘顶点,在MATLAB 2020b软件中对所有局部最高值点进行逐个检查,当一个局部最高值点是指定范围内最高的局部最高值点时,则判断该局部最高值点为沙丘顶点。本研究根据沙丘迎风坡坡度一般不小于10°的现实情况和程序测试经验,参考后文搜索距离设置方法,选定以局部最高值点为中心10°为阈值的搜索范围作为认定沙丘顶点的指定范围。
距离-高度曲线:以顶点为中心,将搜索距离内的局部最低值点按照距离由近及远进行排列,得到局部最低值点到沙丘顶点的距离-高度曲线。
距离-贡献曲线:在距离-高度曲线的基础上,从顶点出发,由近及远,如果一个局部最低值点的高程值大于前一个局部最低值点的高程值,则把当前局部最低值点的高程值设为前一个点的高程值,修改后的高程值可用于描述这个局部最低值点对沙丘相对高度的贡献,得到局部最低值点到沙丘顶点的距离-贡献曲线。
贡献效率:将距离-贡献曲线上某点与前一点的水平距离与高差形成的坡度定义为该点对沙丘相对高度的贡献效率。参考前文关于斜坡的讨论,本研究规定贡献效率≥5°则该点对沙丘相对高度的贡献有效,反之则为无效。
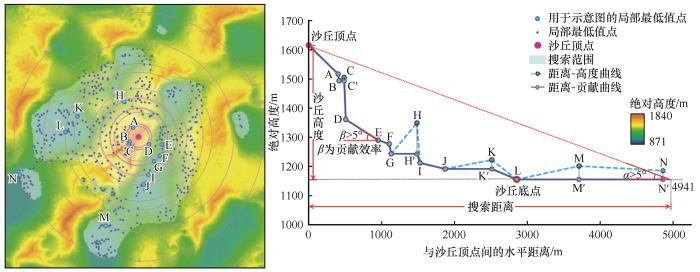
沙丘底点:在搜索距离内,计算所有局部最低值点的贡献效率,从沙丘顶点出发,由近及远,最后一个贡献有效的局部最低值点即为沙丘底点(图2)。
图2
图2
沙丘底点选取算法示意图
Fig.2
Schematic diagram of the algorithm for dune base point selection
1.3 数据
AW3D30(ALOS World 3D)v3.1版本数据。由日本宇宙航空研究开发机构(Japan Aerospace Exploration Agency, JAXA)开发,空间分辨率为30 m,设计高程精度为5 m,在相同分辨率的全球DSM/DEM数据产品中处于领先水平[31](
SRTM(Shuttlc Radar Topography Mission)v4.1版本数据。由NASA、NIMA和DLR共同合作的国际项目开发,空间分辨率为3''(约90 m),绝对高程精度优于16 m,相对高程精度优于10 m(
ASTER GDEM(The Advanced Spaceborne Thermal Emission and Refiection Radiometer Global DEM)v3版本数据。是美国航空航天局(NASA)和日本宇宙航空研究开发机构(JAXA)共同开发的数字高程模型(DEM)。该模型使用来自ASTER卫星的光学数据,覆盖了整个地球的陆地表面,具有1''(约30 m)的空间分辨率,高程精度20 m[31](
1.4 误差来源和处理方法
误差可以分为系统误差、偶然误差以及粗差[32]。
系统误差是由某些特定因素影响而产生的有规律的,但通常难以彻底消除的系统性误差[32],本研究算法的系统误差主要来自5个方面:①数据本身的系统误差,这是传感器及数据生产过程中产生的系统误差,不在本研究考虑范围之内。②数据水平分辨率对区域内沙丘相对高度统计特征的系统性影响,数据水平分辨率越高,记录的地形起伏越精细,能识别出的沙丘个数就越多,而增多的部分主要是小沙丘,因此水平分辨率对整个沙漠沙丘相对高度的统计特征有系统性的影响;这是数据本身造成的局限性,可以通过剔除低于某个相对高度的所有沙丘的办法来避免统计偏差。③数据高程精度对沙丘相对高度统计特征的系统性影响,数据高程精度不足会导致对地形细节描述不精准,并引入更多噪声点,这将可能使算法将噪声点识别成小沙丘,进而影响沙丘相对高度统计特征;这也是数据自身局限性引起的,也可以通过剔除低于某个相对高度的所有沙丘的办法来避免统计偏差。④本研究提出的算法因为理论与其他算法不同而形成的系统性偏差,比如,若有另外一种沙丘底点选取方法,称“沙丘底点是沙丘背风坡一侧丘间洼地的最低点”,那么本研究得到的沙丘相对高度可能会系统性地比其结果偏高,因为本研究搜索沙丘底点的距离更远,也就更容易找到更低的底点;这部分系统误差本研究暂不予考虑,因为作者认为本研究的算法优于已有方法,后文的分析中也有论证,这部分误差会在未来出现更恰当的沙丘底点选取理论后进行修正。⑤本研究提出的算法中存在一些默认参数,如果做了修改会系统性地影响结果,比如搜索距离和贡献效率都涉及参数“5°”,如果设置更小,则沙丘相对高度会系统性地比目前的结果更高;对这部分误差,本研究也暂不予考虑,因为现有的参数设置是参照已有的地貌分类标准且经实测符合实地情况的,如果在一些特殊地区本研究所设参数经实测不符合实际,则根据实测数据适当调整参数即可。
偶然误差是在测定过程中各种随机因素的偶然性影响而产生的误差[32],在本研究算法中偶然误差主要有:①DEM预处理过程中的误差,这一部分误差主要受人为主观因素的影响,使用高分辨率遥感影像、提高操作人员的熟练程度可以改善,但无法量化,因此不做分析。②数据高程误差在水平方向的影响,在水平方向上,数据的高程误差会导致搜索范围的变化,搜索范围变化后算法选取的沙丘底点可能会有所不同,最终将误差引入到沙丘相对高度之中;可以将沙丘顶点增加一个误差单位(如,AW3D30、ASTER GDEM、SRTM分别增加5、17、16 m),然后重新识别沙丘底点,以此描述高程误差在水平方向上通过影响沙丘底点的选择而对沙丘相对高度的影响。③数据高程误差在垂直方向的影响,数据本身的误差影响了沙丘顶点与底点的绝对高度数值,因此会造成沙丘相对高度的误差。间接测量误差评定时,一般是根据直接测得的多个自变量值的精度来评定间接测量的因变量的精度,即利用误差传递定律测定因变量的误差[33]。沙丘相对高度是沙丘顶点与底点高程的差值,使用误差传递定律时,因为自变量(顶点高程值、底点高程值)的个数与测量次数都很少,因此应当使用极限误差来评定因变量(沙丘相对高度)的误差[33]。
式中:ξymax是因变量的误差;|D1|和|D2|是各自变量误差的绝对值。因此,沙丘相对高度的极限误差是沙丘底点与顶点的高程误差的绝对值之和,沙丘顶点与底点的高程误差等于数据源的高程精度。
粗差主要是由条件异常变化产生的误差[32],这种误差一般情况下从宏观来说对数据整体的影响不及系统误差和偶然误差。本研究算法的粗差主要有两个来源:①数据预处理存在失误,比如DEM上没有被剔除的石质山体可能会被当做沙丘识别出来,这种情况下,如果山体相对高度与沙丘相差不多,则影响可以忽略,如果山体相对高度明显偏高,则可以在得到计算结果后,将数据按沙丘相对高度排序,结合高分辨率影像从沙丘相对高度的最大值开始按顺序逐个进行粗差检查,推荐检查前20个,但由于数据预处理效果不同,此数值需要根据实际情况确定。②数据异常值,数据异常值在宏观上对沙丘相对高度空间分布影响不大,在局部上,本研究算法识别出的每个沙丘都是相互独立的,都有各自的搜索范围,异常值能影响到的周边沙丘的数量非常有限,这种影响也不会累积和扩散,对于受影响的个别沙丘,与第一种粗差类似,如果沙丘相对高度与整个沙漠其他沙丘相差不多,则不需要特别处理,如果明显偏高,则在粗差检查中可以被发现,直接剔除或修正数据异常值即可。
2 结果与分析
2.1 整个沙漠沙丘相对高度的统计特征
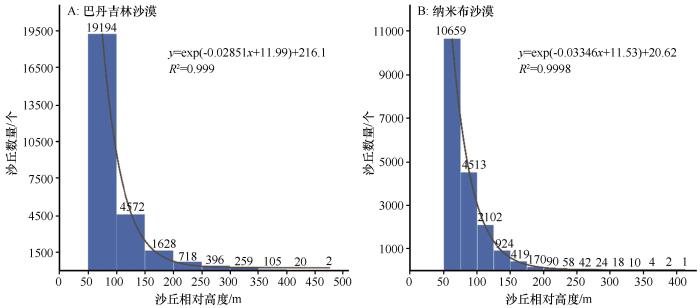
在DEM水平分辨率为30 m时,相对高度50 m以上的沙丘的形态才能被较为准确地描述出来[10],所以在讨论沙丘相对高度统计特征时主要分析相对高度大于等于50 m的数据。在AW3D30数据上分别计算巴丹吉林沙漠和纳米布沙漠的沙丘相对高度,对50~500 m的沙丘相对高度数据做统计直方图(图3),结果显示沙丘数量随着相对高度的增加而减少。沙丘相对高度的统计直方图均符合负指数函数特征(R2分别为0.999和0.9998),沙丘相对高度均集中于50~100 m,占比分别为71.37%和79.70%,但巴丹吉林沙漠高大沙丘比纳米布沙漠更多,300 m以上的沙丘有378个,占比为1.41%,而纳米布沙漠300 m以上的沙丘有32个,占比仅为0.17%,比巴丹吉林沙漠低一个数量级,此外,巴丹吉林沙漠最大沙丘相对高度(461 m)远高于纳米布最大沙丘相对高度(402 m)。
图3
以上统计表明本研究算法可以用于研究整个沙漠沙丘相对高度的统计特征,为沙丘形态学研究提供更精细、更完整的数据,这是基于数字地形分析方法计算沙丘相对高度比传统人工测量方法所具有的独特优势。
2.2 同一区域内不同数据源对沙丘相对高度统计特征的影响
分别使用AW3D30数据、SRTM数据以及ASTER GDEM数据对同一沙漠小区域的沙丘进行识别计算,结果如表2所列。AW3D30、SRTM、ASTER数据源下的沙丘相对高度分别为85±118、169±118、44±76 m,相对高度区间分别为4~461、9~406、44~465 m,中位数分别为24、147、22 m。AW3D30数据和ASTER GDEM数据的水平分辨率相近,差别主要是AW3D30的高程精度(5 m)远优于ASTER的高程精度(17 m),统计结果显示,ASTER识别出的沙丘数量(311个)远多于AW3D30识别出的沙丘数量(121个),主要是绝对高度较低且相对高度低于50 m的沙丘达到AW3D30的3.4倍,而对高大沙丘,尤其是300 m以上的沙丘,二者识别的数量几乎完全一致,且最大沙丘的高度也相差很少(分别为465 m和461 m),这表明就AW3D30和ASTER两种数据而言,高程精度对相对高度300 m以上的沙丘几乎没有影响,误差主要体现在沙丘高度小于50 m的部分,高程精度不足会导致这些小沙丘数量偏多2.4倍。SRTM数据虽然设计的高程精度是16 m,但实际研究发现其高程精度优于9 m[31],因此SRTM数据和AW3D30数据的主要区别是水平分辨率的区别(分别为90 m和30 m),统计结果显示,SRTM数据识别出的沙丘数量仅为AW3D30数量的约35.5%,这主要是水平分辨率不足无法描述小沙丘导致的,300 m以上沙丘个数(8个)是AW3D30结果(12个)的2/3,这应该是水平分辨率不足时大沙丘形态描述不准确导致的,比如SRTM得到的最大沙丘高度(406 m)比AW3D30数据的结果(461 m)偏低55 m。这表明就AW3D30和SRTM两种数据而言,水平分辨率不足会导致小沙丘无法体现(50 m以下小沙丘个数少了88.5%),大沙丘高度整体偏低(最大沙丘高度低了55 m)、数量整体偏少(300 m以上沙丘数量少了1/3)。
表2 同一小区域不同数据源沙丘个数
Table 2
| 沙丘高度/m | 数据源 | ||
|---|---|---|---|
| AW3D30 | SRTM | ASTER | |
| 合计 | 121 | 43 | 311 |
| 绝对高度 | |||
| 1 100~1 200 | 33 | 4 | 83 |
| 1 200~1 300 | 48 | 7 | 203 |
| 1 300~1 400 | 21 | 12 | 9 |
| 1 400~1 500 | 6 | 10 | 5 |
| 1 500~1 600 | 11 | 10 | 8 |
| 1 700~1 800 | 2 | 0 | 3 |
| 合计 | 121 | 43 | 311 |
| 相对高度 | |||
| 0~50 | 78 | 9 | 264 |
| 50~100 | 12 | 7 | 23 |
| 100~150 | 7 | 6 | 5 |
| 150~200 | 4 | 3 | 1 |
| 200~250 | 4 | 5 | 7 |
| 250~300 | 4 | 5 | 0 |
| 300~350 | 3 | 5 | 2 |
| 350~400 | 5 | 2 | 5 |
| 400~450 | 2 | 1 | 2 |
| 450~500 | 2 | 0 | 2 |
2.3 不同高程精度对同一沙丘相对高度的影响
数据高程精度对沙丘相对高度的影响分为两种:一是沙丘顶点高程与底点高程相减计算相对高度时,高程精度通过误差传递定律带给沙丘相对高度的误差;二是沙丘顶点高程数值的变化会引起搜索范围的变化,可能导致算法选取的沙丘底点发生变化,进而带来沙丘相对高度计算的误差。
对第1种误差,以AW3D30、ASTER、SRTM数据源计算的沙丘相对高度的极限误差分别为10、34、32 m。
对于第2种误差,本研究用3种数据源计算了同一个沙丘的相对高度,然后在3种数据源上给沙丘顶点位置的高程值分别都增加一个误差单位(AW3D30、ASTER GDEM、SRTM分别增加5、17、16 m),重新识别沙丘底点,计算沙丘相对高度(表3):①本算法使用相同数据源在其最大误差条件下所识别的沙丘顶点与底点均相同,说明相同数据源下,数据的高程误差不会影响沙丘底点的选择。②本算法使用不同数据源得到的同一沙丘顶点与底点的坐标及沙丘相对高度数值均有所不同。若以AW3D30数据识别的沙丘顶点(551 567,4 415 800)、沙丘底点(5 487 118,4 415 991)为准,则ASTER数据识别的沙丘顶点与底点偏差较小(水平距离分别为34 m和348 m),而SRTM数据识别的沙丘顶点偏差较小而底点偏差较大(水平距离分别为83 m和3 557 m)。可以认为就这3种数据而言,在水平分辨率相近的情况下,本算法识别到的同一沙丘的顶点和底点位置是一致的,相对高度的差别主要是极限误差引起的,在分辨率不同的情况下,沙丘顶点位置相近而沙丘底点的选择可能并不一致,这主要是不同水平分辨率下数据对地形的描述本身存在差异导致的。此时沙丘相对高度的误差由两部分组成:一是沙丘相对高度计算过程的极限误差,二是因地形描述差异导致的误差。
表3 不同数据源下识别同一沙丘的统计信息
Table 3
| 指标 | AW3D30 | AW3D30 (调整顶点后) | ASTER | ASTER (调整顶点后) | SRTM | SRTM (调整顶点后) |
|---|---|---|---|---|---|---|
| 沙丘顶点绝对高度/m | 1 616 | 1 616 | 1 624 | 1 624 | 1 573 | 1 573 |
| 数据源的误差/m | 5 | 5 | 17 | 17 | 16 | 16 |
| 沙丘顶点绝对高度/m(调整后) | — | 1 621 | — | 1 641 | — | 1 589 |
| 搜索距离/m | 4 941 | 4 999 | 5 182 | 5 347 | 4 479 | 4 718 |
| 沙丘绝对高度/m | 1 616 | 1 621 | 1 624 | 1641 | 1 573 | 1 589 |
| 沙丘相对高度/m | 461 | 466 | 465 | 482 | 389 | 405 |
| 搜索范围的面积/m | 32 716 417 | 33 800 964 | 35 556 949 | 39 803 180 | 25 642 515 | 28 507 286 |
| 沙丘底点横坐标/m | 548 718 | 548 718 | 548 776 | 548 776 | 551 760 | 551 760 |
| 沙丘底点纵坐标/m | 4 415 991 | 4 415 991 | 4 416 334 | 4 416 334 | 4 414 148 | 4 414 148 |
| 沙丘顶点横坐标/m | 551 567 | 551 567 | 551 532 | 551 532 | 551 509 | 551 509 |
| 沙丘顶点纵坐标/m | 4 415 800 | 4 415 800 | 4 415 800 | 4 415 800 | 4 415 740 | 4 415 740 |
2.4 沙丘相对高度的空间分布
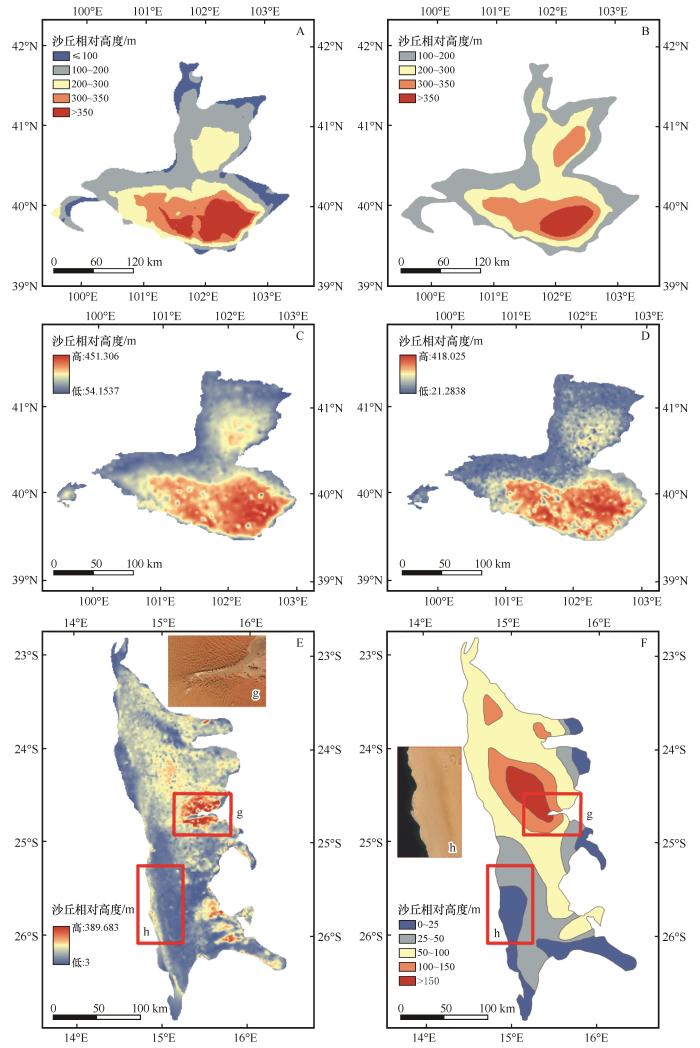
将本研究算法分别在巴丹吉林沙漠、纳米布沙漠计算的沙丘相对高度与前人研究结果进行对比(图4),为便于对比,本研究结果用前人划定的边界分别进行了裁剪,且使用了相似的可视化表达方法。①本研究的巴丹吉林沙漠、纳米布沙漠沙丘相对高度空间分布与前人研究结果基本一致。两个沙漠的沙丘相对高度均呈环带状自腹地向边缘递减,最高大沙丘分别存在于巴丹吉林沙漠东南腹地、纳米布沙漠东北腹地;巴丹吉林沙漠整体格局呈现东高西低,南高北低;纳米布沙漠整体格局呈现东高西低,北高南低。②从空间分布的细节上来说,本研究与汪克奇等[14]的研究均使用了数字地形分析方法,得到的空间分布图较人工测量结果更加精细,能体现更多空间分布特征的细节变化。③本研究与Lancaster[6]计算的纳米布沙漠沙丘相对高度空间分布图在部分区域存在明显差异。高分辨率影像显示:图4g区域干涸河道两侧存在明显的高大沙丘,且可能是整个沙漠最高大的沙丘,Lancaster[6]的结果中对此没有体现,本研究结果则可以很好地体现这一特征;图4h区域靠近海岸的沙丘高度分布并非弧形分布,而是条状分布,沙丘相对高度是海岸高于腹地,而不是腹地高于海岸,Lancaster[6]的结果与影像不符,本研究结果与影像一致。综上,本研究算法计算的沙丘相对高度在总体格局上与前人结果一致,但细节上更加精细和准确。
图4
图4
本研究(A、C、E)与前人研究(B、D、F)计算沙丘相对高度空间分布对比
Fig.4
Comparison of spatial patterns of relative dune heights: this study (A, C, E) and previous studies (B, D, F)
2.5 沙丘相对高度的数值对比
图5
表4 巴丹吉林沙漠最大沙丘相对高度
Table 4
3 结论
针对沙丘相对高度测量中沙丘底点选取的问题,本研究提出贡献效率的概念,并利用贡献效率给出了从众多地形局部最低值点中选取沙丘底点的方法,据此可进一步得到沙丘相对高度。用本研究的算法在巴丹吉林沙漠和纳米布沙漠计算了沙丘相对高度,与前人研究结果进行对比验证。
本研究结果与前人研究结果基本一致,而且结果比已有结果更准确、更精细,可以用于识别整个沙漠沙丘相对高度的各种统计特征,并对比这些统计特征在不同沙漠的差异,比传统人工测量方法具有的独特优势。
水平分辨率不同导致SRTM数据识别出的沙丘数量仅为AW3D30数量的约35.5%,50 m以下小沙丘个数少了88.5%,300 m以上高大沙丘个数少了1/3;高程精度的差别对相对高度300 m以上的沙丘几乎没有影响,误差主要体现在沙丘高度小于50 m的部分,ASTER GDEM数据上这些小沙丘数量比AW3D30数据偏多2.4倍;在水平分辨率相近的情况下,本算法识别到的同一沙丘的顶点和底点位置是一致的,相对高度的差别主要是极限误差引起的,在水平分辨率不同的情况下,沙丘底点的选择可能并不一致。
本研究在巴丹吉林沙漠计算的沙丘相对高度与前人研究结果基本保持一致,并且至少在最大沙丘的相对高度(461±10 m)方面比已有算法的结果更加接近前人实测值。
相比前人遥感测量算法,本研究算法仅需数字地形数据,减少了对额外数据的依赖,且不需要划分沙丘类型,减少了算法中主观因素的干扰。
因此,本研究算法在保持较强可信度的基础上提高了测量的效率和客观性,算法基于贡献效率计算沙丘底点,可实现大范围、客观、全自动的沙丘相对高度测量。本算法不依赖地形数据之外的其他数据,使得对全球沙漠沙丘相对高度研究成为可能,尤其在无人区沙丘形态测量方面具有明显优势,且为全球沙漠沙丘形态学研究提供了基于数字地形分析方法提取沙丘形态指标的新思路。此外,本研究算法所选定的沙丘底点可以用于对某一沙丘相对高度的实地精确测量,提高实测相对高度时沙丘底点选取的客观性。
参考文献
Morphometric analysis of aeolian bedforms in the Namib Sand Sea using ASTER data
[J].
Exploring the contributions of vegetation and dune size to early dune development using unmanned aerial vehicle (UAV) imaging
[J].
Geomorphological hierarchies for complex mega-dunes and their implications for megadune evolution in the Badain Jaran Desert
[J].
Formation of the highest sand dunes on Earth
[J].
Geomorphology of the megadunes in the Badain Jaran Desert
[J].
What sets aeolian dune height?
[J].
The shape of the barchan dunes of Southern Morocco
[J].
Barchans of Minqin:morphometry
[J].
柴达木盆地西南缘山前沙丘区沙丘地貌形态特征
[J].
基于遥感影像的新月形沙丘动态监测
[J].
中国地貌全图研制
[J].
Slope unit-based genetic landform mapping on Tibetan plateau-a terrain unit-based framework for large spatial scale landform classification
[J].
Evolution of megadunes and lakes in the Badain Jaran Desert,Inner Mongolia,China during the last 31,000 years
[J].
Contribution of lake-dune patterning to the dune height of mega-dunes in the Badain Jaran Sand Sea,Northern China
[J].




 甘公网安备 62010202000688号
甘公网安备 62010202000688号