0 引言
沙丘作为风成床面广泛分布的重要地貌类型,是气流与沙质下垫面相互作用的产物,是风沙地貌学研究的主要对象[1-2]。根据合成输沙势与沙丘脊线之间的夹角(Φ),可将沙丘划分为横向沙丘(Φ≥75°)、斜向沙丘(15°<Φ<75°)以及纵向沙丘(Φ≤15°)[3]。新月形沙丘是横向沙丘的一种,也是风沙地貌中最基本的地貌单元,因其形似新月而得名。新月形沙丘主要形成于窄单峰风况且沙源供给不足的区域,分布在世界各大沙漠的边缘、河谷、干涸盐湖、海岸及地外星球[3-5]。气流是引起沙粒起动及输移的外因,对新月形沙丘的塑造起着至关重要的作用。根据沙丘形态对气流的影响,可以把新月形沙丘的流场分为3个区域:迎风坡区、背风坡区和丘间地[6]。新月形沙丘迎风坡坡脚至沙丘顶部的气流加速与沙丘迎风坡坡度和高度有密切的关系[7-8]。沙丘背风坡气流也可分为涡流区、保护区和尾流恢复区[9]。尾流重新附着点的位置是确定涡流区范围的关键,其与迎风坡的形态密切相关,众多研究结果发现尾流附着点位于4~15倍沙丘高度的位置[10-21]。
以往学者对沙丘流场的研究主要是利用野外观测和风洞实验的方法[9, 22-27]。野外观测是最为直接的一种研究方法,但是受时间和空间制约,观测有诸多不便,而且在时空尺度上,实验设计和数据处理非常复杂,并且受到测量仪器的限制,难以获得沙丘表面整个流场的详细信息。风洞实验不受自然条件的制约,可以随时获得稳定的实验条件与实验环境,较好地模拟与野外相似的流场环境,但是在满足相似性条件时,难以同时保证几何相似、运动相似和动力相似,通常风洞模拟实验都是不完全相似的[4]。学界对新月形沙丘迎风坡的流场关注较多[28],而新月形沙丘背风坡流场由于其存在高度的气流湍动,导致流场结构十分复杂,加之复杂的野外环境和测量仪器精度的限制,造成野外观测和风洞实验都很难对流场进行详细的分析并获得令人满意的结果。
目前随着计算机技术的发展,计算流体力学方法(Computational Fluid Dynamics,CFD)可以很好地解决上述困难。Parsons等[29]采用RNG k-ε湍流模型模拟了理想横向沙丘二维气流并与风洞实验数据进行了对比验证,较为准确地预测了沙丘上方的气流流动模式。Liu等[10]对比了二维和三维横向沙丘CFD模拟的结果,三维模型显示出了在二维模型中无法体现的明显横向气流。Smyth等[30]对复杂风蚀坑内的气流进行了CFD模拟,结果表明测量数据和模拟数据总体上具有良好的一致性。Smith等[31]对实地新月形沙丘的三维气流进行了CFD模拟,发现背风面的湍流模式为两个反向旋转的漩涡。虽然已经有学者对各种类型的沙丘进行过CFD的模拟研究,但对新月形沙丘表面流场尤其是涡流区复杂流动结构的认识仍不全面,缺乏新月形沙丘形态和来流风速对流场结构影响的总结与归纳。本文拟设置不同的新月形沙丘形态参数和不同的来流风速,对新月形沙丘表面流场进行详细的分析,探明沙丘高度、迎风坡坡度和来流风速对沙丘表面流场的影响,研究结果可以加深学界对新月形沙丘形成演变机制的认识,丰富风沙地貌学基础理论,亦可为干旱区防风固沙工程提供科学依据。
1 方法
本文模拟均使用计算流体力学软件Fluent 2020 R1完成,计算网格由Fluent Meshing网格工具生成,求解计算由Fluent Solution求解器完成。
1.1 计算模型与求解控制
1.2 计算域及网格划分
为消除计算域边界对模拟结果可能存在的潜在影响,计算域边界应设置在距沙丘模型足够远的位置。经试算,确定计算域入口距沙丘模型的距离为沙丘高度的10倍,计算域出口距沙丘模型的距离为沙丘高度的70倍,计算域高度为沙丘高度的10倍。计算网格采用六面体核心网格,首先在计算域表面生成面网格,然后在面网格的基础上生成Poly-Hexcore多面体和六面体混合体网格。本次模拟的研究重点为沙丘表面附近区域,该区域也是流场中速度梯度最大的区域,因此在该区域进行网格加密,网格最小尺度为沙丘表面第一层网格(取值在2.1节处进行介绍),边界层网格设置3层,计算域内网格最大尺度为2 m,按网格膨胀比1.05进行过渡。
1.3 边界条件
模拟计算域出口为压力出口(Pressure-Outlet)边界条件,计算域顶面及两侧面采用对称(Symmetry)边界条件,计算域底面及沙丘表面采用无滑移壁面(No Slip Wall)边界条件,计算域入口采用速度入口(Velocity-Inlet)边界条件,速度采用对数分布的大气边界层条件[36]。
来流风速:
湍动动能:
湍动动能耗散:
1.4 沙丘尾流区流场分区定义
以新月形沙丘背风侧后一定距离,0.1 m高度处的水平速度由负变为正的位置定义为尾流重新附着点。尾流重新附着点是确定涡流区的重要位置,对沙粒的运动有着重要的影响。水平风速由零达到临界起沙风速的位置定义为保护区,由拜格诺提出的临界起沙风速与沙粒粒径(经过对现场采集的沙粒样本进行的粒度分析,取值为0.11 mm)的关系式可以计算出0.1 m高度处的临界起沙风速为4.70 m·s-1[38]。气流继续恢复到达初始气流状态的位置为尾流恢复区。
2 CFD模拟验证与实验设置
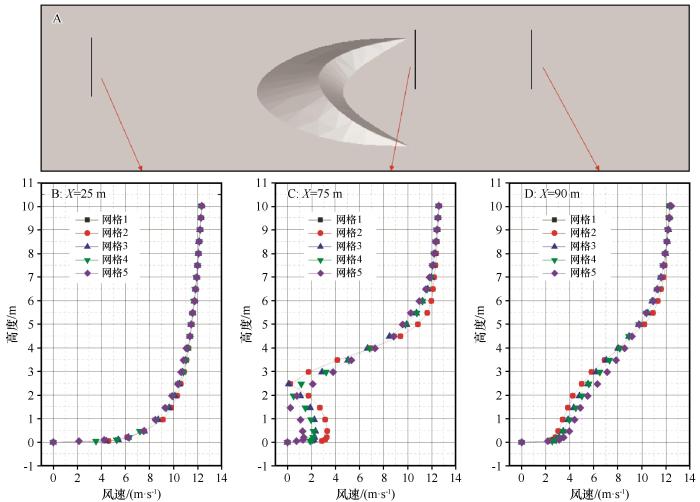
2.1 网格无关性验证
表1 5种不同尺度的网格详情
Table 1
| 网格 | 第一层网格高度/m | 网格数 |
|---|---|---|
| 网格1 | 0.05 | 401 813 |
| 网格2 | 0.025 | 436 577 |
| 网格3 | 0.0125 | 614 183 |
| 网格4 | 0.00625 | 825 661 |
| 网格5 | 0.003125 | 1 213 342 |
图1
2.2 模拟与实测数据的对比验证
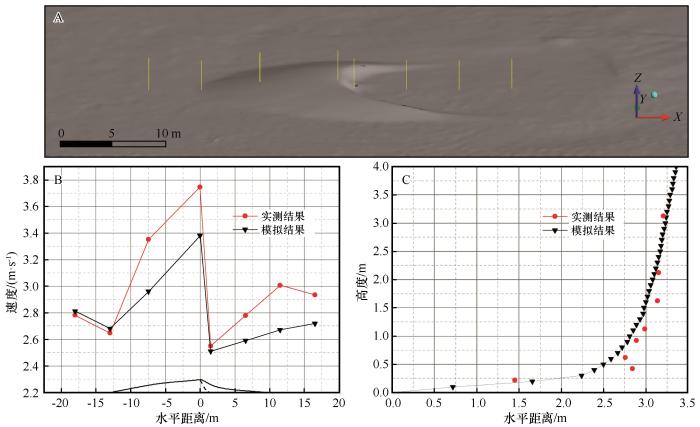
为验证CFD数值模拟结果的可靠性,于2021年10月在塔克拉玛干沙漠东部边缘一处(39.462°N、88.444°E)采集了一个典型新月形沙丘的三维地形及其在沙尘暴中的部分点位风速数据。
沙丘地形数据的野外测量采用大疆精灵4 RTK(P4R)无人机完成。该无人机系统由一套精灵4 RTK (P4R)无人机和一套中海达Ubase无人机地面站组成。其中,无人机系统负责采集样区地貌特征及定位信息,Ubase作为地面基站,能够精确获取卫星定位信息。飞行采用了3D五向地形测量模式,飞行高度25 m,航向和旁向重叠率分别为80%和75%。整个区域单架次实现全覆盖。考虑到本研究目标对地理精度的要求不高,因此,测量过程中未进行控制点的布设。
沿沙丘迎风坡前、坡脚、坡中、坡顶和后部尾流区的一条断面布设二维超声风速仪,沙丘形态及布设示意图如图2A,采样频率1 min,测量距地表0.3 m处的二维风速。之所以选择这一高度,是因为0.3 m的高度既可以尽可能捕捉到近地表气流的运动情况,又可以避免跃移沙粒对超声传感器信号的干扰,致使数据丢失。此外在离该新月形沙丘50 m距离处设有长期观测气象站,可以获取当时当地3 m高度内的8层风速值(测量高度分别为0.22、0.42、0.62、0.92、1.12、1.62、2.12、3.12 m)。
图2
图2
野外风速仪布设示意图及实测数据与CFD数值模拟的对比
Fig. 2
Layout diagram of field anemometer and the comparison of field measurement and CFD numerical simulations
2.3 CFD模拟实验设置
新月形沙丘高度、沙丘迎风坡坡度和来流风速对沙丘周围流场结构有着重要的影响。新月形沙丘的形态参数包括长、宽、高、翼角、迎风坡、背风坡和沙脊线,其横截面呈抛物线状[39]。新月形沙丘两侧的翼角沿顺风向延伸;沙丘迎风坡坡度8°~20°;背风坡坡度28°~34°,相当于沙粒的最大休止角[6];高度差异较大[40],宽高比相对固定,介于9°~18[15,40]。依据前人对新月形沙丘形态特征的研究成果,设定了不同的沙丘高度、迎风坡坡度和来流风速进行模拟计算,详细参数设置见表2。选取两种不同的新月形沙丘几何模型,一种为迎风坡坡度15°、背风坡坡度34°和沙丘宽高比10固定,沙丘高度以0.4 m为步长,从1.2 m递增到4.8 m;另一种为沙丘高度3.2 m、背风坡坡度34°和沙丘宽高比10固定,迎风坡坡度以2°为步长,从8°递增到20°。
表2 CFD模拟实验参数
Table 2
| 不同沙丘高度 | |||||||
|---|---|---|---|---|---|---|---|
| 高度/m | 迎风坡坡度/(°) | 迎风坡长度/m | 背风坡坡度/(°) | 背风坡长度/m | 翼长/m | 沙丘宽度/m | 摩阻风速/(m·s-1) |
| 1.20 | 15.00 | 6.81 | 34.00 | 1.78 | 4.80 | 12.00 | 0.50 |
| 1.60 | 15.00 | 9.07 | 34.00 | 2.37 | 6.40 | 16.00 | 0.50 |
| 2.00 | 15.00 | 11.34 | 34.00 | 2.97 | 8.00 | 20.00 | 0.50 |
| 2.40 | 15.00 | 13.61 | 34.00 | 3.56 | 9.60 | 24.00 | 0.50 |
| 2.80 | 15.00 | 15.88 | 34.00 | 4.15 | 11.20 | 28.00 | 0.50 |
| 3.20 | 15.00 | 18.15 | 34.00 | 4.74 | 12.80 | 32.00 | 0.50 |
| 3.60 | 15.00 | 20.42 | 34.00 | 5.34 | 14.40 | 36.00 | 0.50 |
| 4.00 | 15.00 | 22.69 | 34.00 | 5.93 | 16.00 | 40.00 | 0.50 |
| 4.40 | 15.00 | 24.95 | 34.00 | 6.52 | 17.60 | 44.00 | 0.50 |
| 4.80 | 15.00 | 27.22 | 34.00 | 7.12 | 19.20 | 48.00 | 0.50 |
| 不同迎风坡坡度 | |||||||
| 高度/m | 迎风坡坡度/(°) | 迎风坡长度/m | 背风坡坡度/(°) | 背风坡长度/m | 翼长/m | 沙丘宽度/m | 摩阻风速/(m·s-1) |
| 3.20 | 8.00 | 22.77 | 34.00 | 4.74 | 12.80 | 32.00 | 0.50 |
| 3.20 | 10.00 | 18.15 | 34.00 | 4.74 | 12.80 | 32.00 | 0.50 |
| 3.20 | 12.00 | 15.05 | 34.00 | 4.74 | 12.80 | 32.00 | 0.50 |
| 3.20 | 14.00 | 12.83 | 34.00 | 4.74 | 12.80 | 32.00 | 0.50 |
| 3.20 | 16.00 | 11.16 | 34.00 | 4.74 | 12.80 | 32.00 | 0.50 |
| 3.20 | 18.00 | 9.85 | 34.00 | 4.74 | 12.80 | 32.00 | 0.50 |
| 3.20 | 20.00 | 8.79 | 34.00 | 4.74 | 12.80 | 32.00 | 0.50 |
| 不同来流风速 | |||||||
| 高度/m | 迎风坡坡度/(°) | 迎风坡长度/m | 背风坡坡度/(°) | 背风坡长度/m | 翼长/m | 沙丘宽度/m | 摩阻风速/(m·s-1) |
| 3.20 | 15.00 | 18.15 | 34.00 | 4.74 | 12.80 | 32.00 | 0.30 |
| 3.20 | 15.00 | 18.15 | 34.00 | 4.74 | 12.80 | 32.00 | 0.35 |
| 3.20 | 15.00 | 18.15 | 34.00 | 4.74 | 12.80 | 32.00 | 0.40 |
| 3.20 | 15.00 | 18.15 | 34.00 | 4.74 | 12.80 | 32.00 | 0.45 |
| 3.20 | 15.00 | 18.15 | 34.00 | 4.74 | 12.80 | 32.00 | 0.50 |
| 3.20 | 15.00 | 18.15 | 34.00 | 4.74 | 12.80 | 32.00 | 0.60 |
| 3.20 | 15.00 | 18.15 | 34.00 | 4.74 | 12.80 | 32.00 | 0.70 |
| 3.20 | 15.00 | 18.15 | 34.00 | 4.74 | 12.80 | 32.00 | 0.80 |
| 3.20 | 15.00 | 18.15 | 34.00 | 4.74 | 12.80 | 32.00 | 0.90 |
| 3.20 | 15.00 | 18.15 | 34.00 | 4.74 | 12.80 | 32.00 | 1.00 |
3 结果
3. 1 沙丘高度对新月形沙丘流场结构的影响
3.1.1 沙丘高度对水平流场结构的影响
图3
图3
不同工况下距离地表0.1 m处计算域中轴线上的水平风速分布(沙丘背风坡坡脚处为X轴的坐标零点)。A为不同沙丘高度工况;C为不同迎风坡坡度工况;E为不同来流风速工况;B、D和F分别为涡流区和保护区与沙丘高度、迎风坡坡度和来流摩阻风速的关系
Fig. 3
The horizontal wind velocity distribution of the axis of the calculation domain at 0.1 m from the barchan dune surface under different working conditions (The zero point of the x-axis coordinates is located in the leeward slope toe of the dune). A: Different dune heights. C: Different windward slope gradients. E: Different inlet velocities. B, D and F are the relationship between vortex zone and protected zone and dune heights, windward slope gradients and inlet shear velocities, respectively
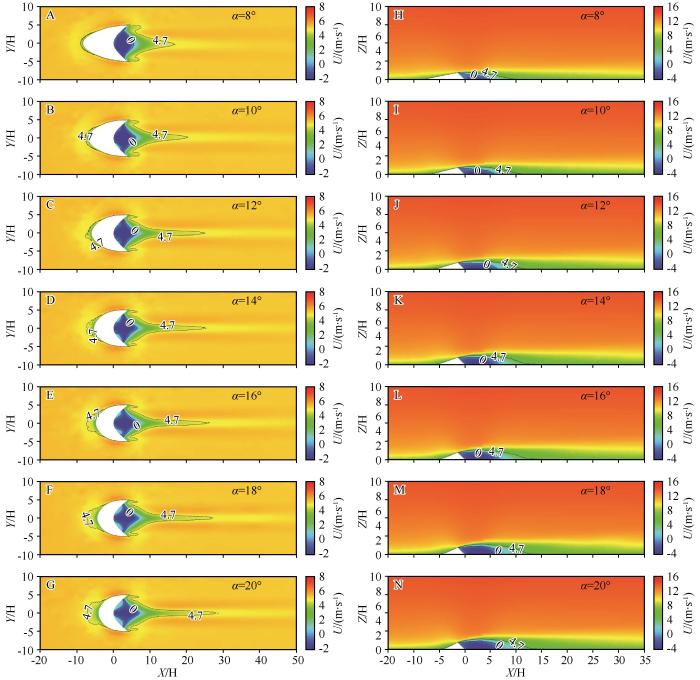
由于尾流涡流区长度与沙丘高度密切相关,为更加直观地展示不同沙丘高度对水平流场产生的影响,将水平距离和垂直距离均以沙丘高度进行无量纲化处理,绘制距地表0.1 m处平面和沙丘中轴线纵剖面的水平速度云图(图4)。气流在经过新月形沙丘迎风坡坡脚时,会出现小范围的减速,这是由于沙丘作为风场中的障碍物,对气流存在阻滞作用,气流向上和向两侧偏转,导致沙丘迎风坡和绕沙丘两侧的气流产生加速效果。不同高度沙丘的背风坡下游涡流区范围变化不明显,这是由于对水平距离进行了无量纲化处理的结果,涡流区长度大致在沙丘高度的5~7倍。涡流区内部水平速度出现负值,说明气流在越过沙丘顶后,发生分离,流向向下偏转,直至气流反向,这也表明涡流区内部气流湍动强烈,流场结构十分复杂。
图4
图4
不同高度新月形沙丘的水平速度分布云图。A~J为距地表0.1 m处平面的水平速度分布云图;K~T为沙丘中轴线纵剖面的水平速度分布云图
Fig. 4
Cloud map of horizontal velocity distribution of barchan dunes with different heights. A-J are horizontal velocity distribution cloud map at 0.1 m from the surface; K-T are horizontal velocity distribution cloud map at the longitudinal profile of the central axis of the dunes
3.1.2 沙丘高度对垂直流场结构的影响
流场中的风速矢量在垂直方向上的分量相比于其水平分量,虽然在数量级上存在着巨大的差别,但同样对沙颗粒的运动具有重要的影响。如图5A~C所示,在沙丘迎风坡上方的垂向风速均大于零,从图中可以看出0.8 m·s-1速度等值线包围的范围超出了迎风坡的范围,并向下游延伸,这就迫使沙颗粒沿沙丘迎风坡向上移动,并越过沙脊线,被气流裹挟传输至下游,其影响范围随着沙丘高度的增加而扩大。越过沙丘顶部的沙颗粒,在自身重力的作用下,落入尾流区并沉积下来,图5中-0.2 m·s-1速度等值线包围的区域表明在涡流区上方存在向下的速度,产生分离流,这更加有利于沙颗粒向地表方向的运动。尾流区近地表和沙丘背风坡垂直速度出现正值,数值和范围均随着沙丘高度的增加而增大,加之其水平速度的反向,使得越过沙丘顶的沙颗粒在下落的过程中被尾流区气流带向与来流风向相反的方向,最终在背风坡一侧沉积下来。
图5
图5
不同工况下新月形沙丘的垂直速度分布云图A~C为不同沙丘高度工况;D~F为不同迎风坡坡度工况;G~I为不同来流风速工况
Fig. 5
Cloud map of vertical velocity distribution of barchan dunes under different working conditions. A-C: Different dune heights;D-F: Different windward slope gradients;G-I: Different inlet velocities
3.2 沙丘迎风坡坡度对新月形沙丘流场结构的影响
3.2.1 沙丘迎风坡坡度对水平流场结构的影响
如图3C和图3D所示,在来流摩阻风速(0.5 m·s-1)和沙丘高度(3.2 m)相同的条件下,当沙丘迎风坡坡度为8°时,尾流附着点出现在沙丘背风坡坡脚下风向16.96 m的位置(沙丘高度的5.3倍),当沙丘迎风坡坡度为20°时,尾流附着点出现在沙丘背风坡坡脚下风向22.37 m的位置(沙丘高度的6.99倍)。可见新月形沙丘迎风坡坡度变化对其尾流区流场结构也有一定影响,沙丘迎风坡坡度增加,尾流附着点随之后移,尾流涡流区范围逐渐增加。从图中也可以看出保护区范围随着沙丘迎风坡坡度的增加而扩大,同时气流也需要更长的距离恢复到相对稳定的初始状态,这与沙丘高度变化对尾流区流场结构的影响规律一致,但影响效果明显减小。
从图6的水平速度分布云图中可以看出在迎风坡坡度较小时,迎风坡前方气流减速区域也比较小,随着坡度的增加,沙丘对气流的阻滞逐渐作用增强,气流减速的区域也明显扩大。沙丘背风侧涡流区长度是沙丘高度的5~7倍,随着坡度的增加,背风侧涡流区长度略有增加,在图中也可以明显看出气流反向的区域不仅长度增加,高度也有明显增加。总体来说沙丘迎风坡坡度对新月形沙丘背风侧流场结构的影响小于对迎风侧流场结构的影响。
图6
图6
不同迎风坡坡度的新月形沙丘水平速度分布云图。A~G为距地表0.1 m处平面的水平速度分布云图;H~N为沙丘中轴线纵剖面的水平速度分布云图
Fig. 6
Cloud map of horizontal velocity distribution of Barchan dunes with different windward slope gradients. A-G are horizontal velocity distribution cloud map at 0.1 m from the surface; H-N are horizontal velocity distribution cloud map at the longitudinal profile of the central axis of the dunes
3.2.2 沙丘迎风坡坡度对垂直流场结构的影响
沙丘迎风坡坡度变化对垂直流场的影响同样主要体现在迎风坡一侧。如图5D~F所示,当沙丘迎风坡坡度为8°时,0.8 m·s-1速度等值线包围的区域基本分布在迎风坡上,没有越过沙脊线,随着迎风坡坡度的增加,沙丘对气流的阻滞作用增加,迎风坡上的气流压缩作用增强,0.8 m·s-1速度等值线包围的区域越过沙脊线向下风向延伸,且包围范围随迎风坡坡度的增加而增大。背风侧-0.2 m·s-1的速度等值线所包围的区域随着坡度的增加逐渐扩大,水平位置随着坡度的增加逐渐向下游移动,垂直位置随着坡度的增加逐渐向上方移动,近地表区域垂直速度出现正值的区域随着坡度的增加而扩大,说明沙丘迎风坡坡度增加导致涡流区范围扩大,沙颗粒越过沙脊线后向背风坡坡脚沉积的效应随之增强。
3.3 来流风速对新月形沙丘流场结构的影响
3.3.1 来流风速对水平流场结构的影响
如图7所示,当来流摩阻风速较小(0.3 m·s-1)时,流场均未达到沙粒起动的风速条件,表明在该条件下流场对新月形沙丘的形态并无塑造作用,随着来流摩阻风速(0.35 m·s-1)的增加,近地表气流首先在沙丘两侧绕流区域到达起动风速,表明沙粒更容易在气流的带动下从新月形沙丘的两侧(即新月形沙丘的两个翼角)传输到下游。随着来流摩阻风速(0.4 m·s-1)继续增加,流场内普遍达到沙粒的起动条件,随后来流风速持续增加,可以很明显地看出,沙丘迎风坡前的气流减速区逐渐缩小,尾流保护区范围也逐渐缩小。这说明来流风速越大,沙丘作为障碍物对流场的影响越小,但更大的来流风速必然会对沙丘形态的塑造造成更大的影响。
图7
图7
不同来流风速下新月形沙丘水平速度分布云图。A~J为距地表0.1 m处平面的水平速度分布云图;K~T为沙丘中轴线纵剖面的水平速度分布云图
Fig. 7
Cloud map of horizontal velocity distribution of barchan dunes under different inlet velocities. A-J are horizontal velocity distribution cloud map at 0.1 m from the surface; K-T are horizontal velocity distribution cloud map at the longitudinal profile of the central axis of the dunes
3.3.2 来流风速对垂直流场结构的影响
图5G~I表明,来流风速对新月形沙丘周围流场垂直速度的影响比较大,在来流摩阻风速较小(0.3 m·s-1)时,0.8 m·s-1速度等值线包围的区域超越了沙脊线,但在迎风坡坡脚处附近却没有分布,随着来流风速的增加,该区域逐渐延伸至坡脚,并布满整个迎风坡,同时该区域整体也随着风速的增加而扩大,并延伸至沙丘背风侧近地表的较大范围内。沙丘背风侧-0.2 m·s-1速度等值线包围的区域随着来流风速的增加明显增大,值得注意的是,该区域出现的位置基本相同,水平方向距沙丘背风坡坡脚下游的长度为沙丘高度的3倍,垂直方向与沙丘高度持平。
4 讨论
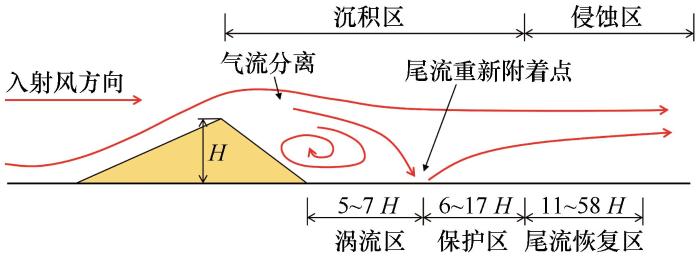
本文意在通过分析流场结构对新月形沙丘的发育机理进行探讨,从图8可直观地看出新月形沙丘表面的流场结构。入射风首先受到沙丘迎风坡的阻挡,向沙丘顶和沙丘两侧偏转,产生气流的加速,在越过沙脊线后,气流发生分离,并在沙丘背风坡一侧产生回流涡,这一区域称为涡流区。近地表的反向气流从尾流重新附着点开始转向下游并逐渐加速,达到起动风速的位置,这一区域称为保护区;随后气流继续加速,沙丘对流场结构的影响越来越小,气流开始恢复至来流的初始状态,这一区域称为尾流恢复区。在涡流区和保护区近地表风速较小,低于沙粒的起动风速,属于沉积区,而尾流恢复区及其下游的区域都属于侵蚀区。
图8
图8
新月形沙丘表面流场结构简图
Fig. 8
Sketch of the flow field structure over the surface of barchan dune
通过分别改变沙丘高度、沙丘迎风坡坡度和来流风速,进行了一系列CFD数值模拟,结果发现沙丘高度、沙丘迎风坡坡度和来流风速均对沙丘表面流场有着重要的影响。涡流区长度随沙丘高度的增大而增大;随迎风坡坡度的增加而增大;基本不因来流风速的改变而改变,长度均大致在沙丘高度的5~7倍,符合前人关于尾流附着点位于4~15倍沙丘高度位置的研究结果[10-21]。对于保护区和尾流恢复区长度,均随着沙丘高度和迎风坡坡度的增加而增大,随来流风速的增大而减小。造成这一结果的原因是,沙丘作为风速场中的一个障碍物,沙丘高度越高,对气流的扰动越强,沙丘迎风坡越大,对气流的阻滞作用越强,自然会对尾流区产生更大的影响;而来流风速越大,气流受到障碍物阻挡的作用就越弱,也更容易恢复到初始的状态。值得注意的是流场与沙丘形态是相互影响、相互制约的,更大的来流风速必然会对沙丘形态产生更大的塑造作用,目前本文数值模拟中暂未考虑新月形沙丘形变这一因素,从沙丘的形变角度出发进行数值模拟将会是未来极具价值的研究主题。
野外实验的设计常常局限于某个单一的二维断面,很难测得沙丘背风侧复杂的湍流运动,而通过CFD的方法可以了解整个流场中非常详细的信息。图9展示了本次模拟中一个算例的三维流线图,该算例中沙丘高度为3.2 m,迎风坡坡度为15°,来流摩阻风速为0.5 m·s-1。图中颜色代表速度矢量在Y轴方向上的分量大小。沙丘背风侧漩涡产生的上升气流可以将从沙脊线逸出的沙颗粒裹挟着带向沙丘背风坡,并沉积下来[27,41]。除了垂直方向的上升气流之外,从图9中还可以清楚地看到在新月形沙丘背风侧近地表处存在两个横向的漩涡,旋转方向相反并沿着沙丘中轴线向两侧扩散,这种特殊的流场结构塑造了新月形沙丘的“新月形”形态,导致沙丘背风坡沉积的沙颗粒向两侧移动到新月形沙丘的两个翼角,并在沙丘两侧加速气流的带动下,逃逸到下游。在自然界中,新月形沙丘通常以集群的方式存在[42-43],且下游沙丘往往出现在上游沙丘一侧翼角的延长线上,Worman等[44]观察到新月形沙丘在移动过程中经常伴随有翼角释放沙粒并形成小新月形沙丘的现象,即“产犊”(calving),这是新沙丘产生的方式之一。本文的工作,从流场的角度解释了上述现象,印证了“下游小新月形沙丘是起源于上游大沙丘一侧翼角损失的沙物质”这一观点[45-46]。那么,如何将单个新月形沙丘的流场特征和新月形沙丘群的流场分布结合起来将是未来研究新月形沙丘形成演化的重点内容。
图9
图9
新月形沙丘周围流场三维流线
Fig. 9
Three-dimensional streamline of the flow field over barchan dune
5 结论
新月形沙丘高度越大,尾流涡流区长度越长,长度为沙丘高度的5~7倍。
新月形沙丘迎风坡坡度越大,尾流涡流区长度越长,长度约为沙丘高度的5~7倍。
来流风速对尾流附着点的位置影响较小,涡流区长度约为沙丘高度的6~7倍。来流风速越大尾流保护区长度越短,沙丘对流场的干扰越小。
在新月形沙丘背风侧近地表处存在两个横向的漩涡,旋转方向相反并沿着沙丘中轴线向两侧扩散,这种特殊的流场结构塑造了新月形沙丘的“新月形”形态,导致沙丘背风坡沉积的沙颗粒向两侧移动到新月形沙丘的两个翼角,并在沙丘两侧加速气流的带动下,逃逸到下游。
参考文献
Sand ripples and dunes
[J].
Storm-controlled oblique dunes of the Oregon coast
[J].
Sand transport model of barchan dune equilibrium
[J].
Wind tunnel and computational study of the stoss slope effect on the aeolian erosion of transverse sand dunes
[J].
Wind tunnel simulation of the aeolian erosion on the leeward side of barchan dunes and its implications for the spatial distribution patterns of barchan dunes
[J].
Numerical simulation of wind flow over transverse and pyramid dunes
[J].
横向沙丘背风侧气流重附风洞模拟
[J].
The geomorphological significance of airflow patterns in transverse dune interdunes
[J].
Turbulent flow over a dune:Green River,Colorado
[J].
Simulation and measurement of surface shear stress over isolated and closely spaced transverse dunes in a wind tunnel
[J].
Width,height and slope relationships and aerodynamic maintenance of barchans
[J].
On the modelling of two-dimensional aeolian dunes
[J].
Toward a model for airflow on the lee side of aeolian dunes
[J].
Turbulence structure over two-dimensional bed forms; implications for sediment transport
[J].
Mean flow and turbulence fields over two-dimensional bed forms
[J].
Air flow and sand transport over sand-dunes
[J].
The wind-induced shaping and migration of an isolated dune:a numerical experiment
[J].
鄂尔多斯高原油蒿(Artemisia ordosica)灌丛沙堆风沙气流结构及其地貌学意义
[J].
反向沙丘近地层气流变化及其对沙丘形态的影响
[J].
坡度和坡形对爬坡沙丘形成影响的风洞模拟实验
[J].
新月形沙丘脊线处的风沙流结构
[J].
Turbulence fields in the lee of two-dimensional transverse dunes simulated in a wind tunnel
[J].
Numerical modelling of airflow over an idealised transverse dune
[J].
Computational fluid dynamic modelling of three-dimensional airflow over dune blowouts
[J].
Three-dimensional airflow and sediment transport patterns over barchan dunes
[J].
The numerical computation of turbulent flows
[J].
A review of Computational Fluid Dynamics (CFD) airflow modelling over aeolian landforms
[J].
Development of turbulence models for shear flows by a double expansion technique
[J].
Renormalization group analysis of turbulence:I.basic theory
[J].
On the use of the k-ε model in commercial CFD software to model the neutral atmospheric boundary layer
[J].
Appropriate boundary conditions for computational wind engineering models revisited
[J].
The shape of the barchan dunes of Southern Morocco
[J].
An empirical-model of aeolian dune lee-face air-flow
[J].
Dynamics of secondary airflow and sediment transport over and in the lee of transverse dunes
[J].
Corridors of barchan dunes:stability and size selection
[J].
A continuous model for sand dunes;review,new developments and application to barchan dunes and barchan dune fields
[J].
Modeling emergent large-scale structures of barchan dune fields
[J].
Field evidence for surface-wave-induced instability of sand dunes
[J].
Simulation of barchan dynamics with inter-dune sand streams
[J].









 甘公网安备 62010202000688号
甘公网安备 62010202000688号