0 引言
本项研究在塔克拉玛干沙漠腹地选取典型新月形沙丘演变监测区,运用华测X90 GNSS接收机的RTK工作模式开展地形三维坐标详测,获得多期精度达毫米级的监测区三维坐标数据。应用地形地籍成图软件CASS 9.0和地理信息数据分析处理软件ArcGIS 10.0,对三维坐标数据进行处理分析,在建立测区DEM的基础上,建立沙丘的三维数字模型并对相邻监测期的三维数字模型进行叠加,利用软件AutoCAD 2010中起点、端点和夹角三要素绘制弧线的方法,实现沙丘对应特征点移动轨迹曲线的拟合。以期对其他流动性沙丘移动轨迹拟合和正确获取移动距离和速度等第一手研究数据资料提供技术和方法支持,并为改进和完善流动性沙丘移动速度计算公式,深入研究流动性沙丘移动速度和移动方向相关的诸多问题奠定基础。
1 研究区概况及数据获取
1.1 研究区概况
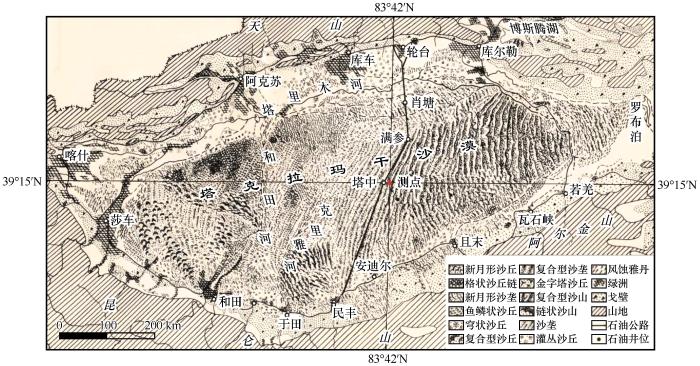
图1
1.2 数据获取
在2015年4月下旬、2015年10月中旬、2016年3月上旬、2016年10月中下旬,分次对沙丘演变监测区共进行4期监测,三维坐标数据采用华测X90 GNSS接收机测量获得(图2)。GNSS接收机由基准站、移动站、数据链、控制软件构成,基准站实时通过数据链以无线电台方式将差分改正信息发送给移动站,移动站接收后即时进行解算处理,获得高精度空间坐标数据。
图2
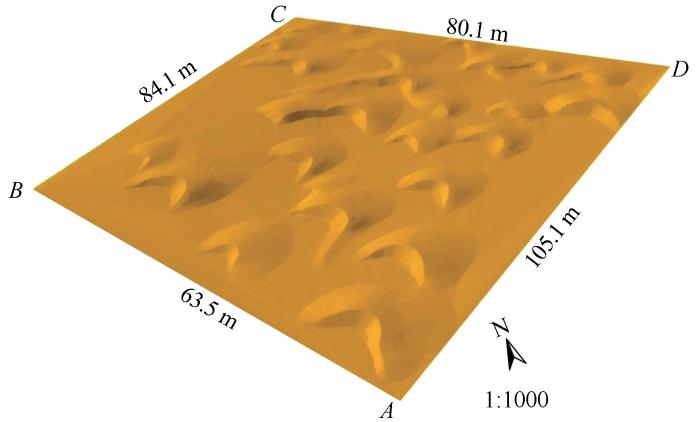
利用华测GNSS接收机测量沙丘表面坐标时,移动站坐标系选用北京54坐标系,测点坐标均基于基准站起算。基准站迁移或在未知点重启后,均可引起起算坐标的变化,为确保基站起算坐标的一致性,基准站迁移或在未知点重启后,均需进行基站平移,以确保测量的移动坐标都具有统一的起算坐标[23-25]。坐标测量时先安装并设置X90 GNSS接收机,确定监测区4个边界点A、B、C和D的位置,选取A点作为基准点,B点作为检测点检验基站平移的准确性(图3)。基于3个不共线点可定面的原理,利用基准站起算点、基准点A和检测点B实现测区的精确定位。沙丘表面测量路径沿图2所示的等高线分布,相邻测点间距约50 cm,在地形陡变部位加大测点密度。
图3
测量时由于手簿和测杆自身重量的影响,测杆陷进沙面的深度难以精确控制,测量者的踩踏也会对沙丘自然表面造成轻微破坏,均可引起测点坐标与实际坐标的误差,影响测量精度。为降低测量误差,在测杆下端固定一块直径5 cm、厚度0.5 cm的圆形橡胶垫,尽量避免测杆下端陷入沙面,同时尽可能使测点避开踩踏过的位置。
2 基于三维数字模型的沙丘移动轨迹拟合
2.1 沙丘三维数字模型的建立
图4
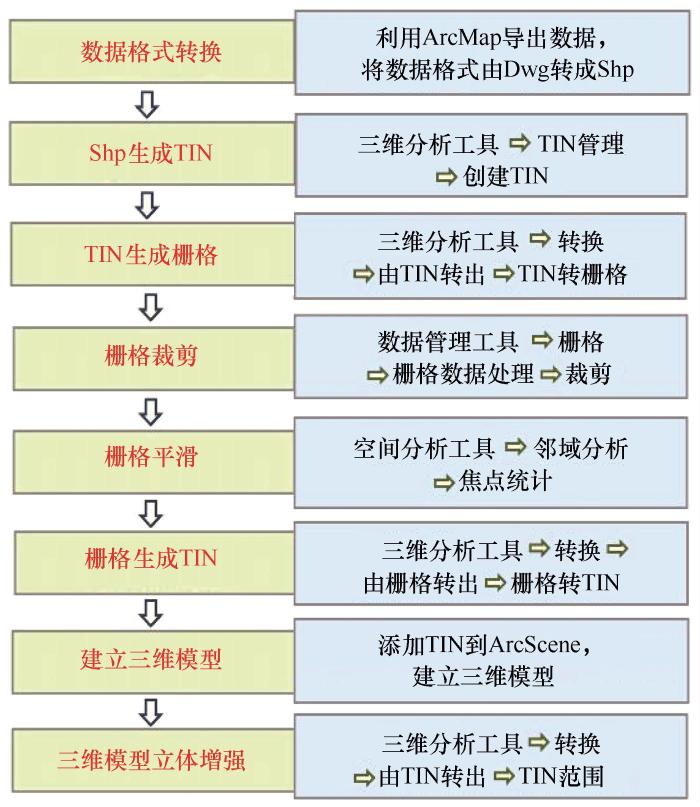
图4
单个沙丘三维模拟技术路线
Fig.4
Technical routes for three-dimensional numerical simulation of a single barchan dune
2.2 沙丘移动轨迹的拟合
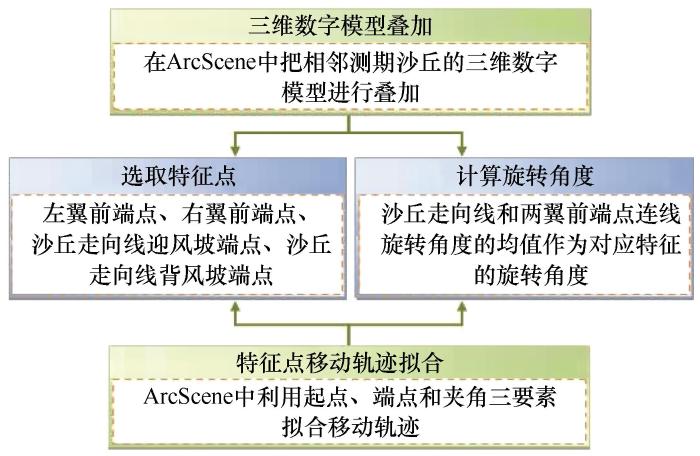
新月形沙丘作为一种流动性沙丘,在风力等多种因素的共同作用下始终处于运动状态。本文以测区典型沙丘D3为例,建立沙丘4个监测期三维数字模型并对相邻测期的三维数字模型进行叠加,在AutoCAD 2010中利用起点、端点和夹角三要素,实现沙丘D3对应特征点移动轨迹曲线的拟合,具体拟合技术路线如图5所示。
图5
图5
沙丘移动轨迹拟合技术路线
Fig.5
Technical routes for moving trajectory fitting of barchan dune
2.2.1 第1、2监测期间沙丘D3移动轨迹的拟合
图6
图6
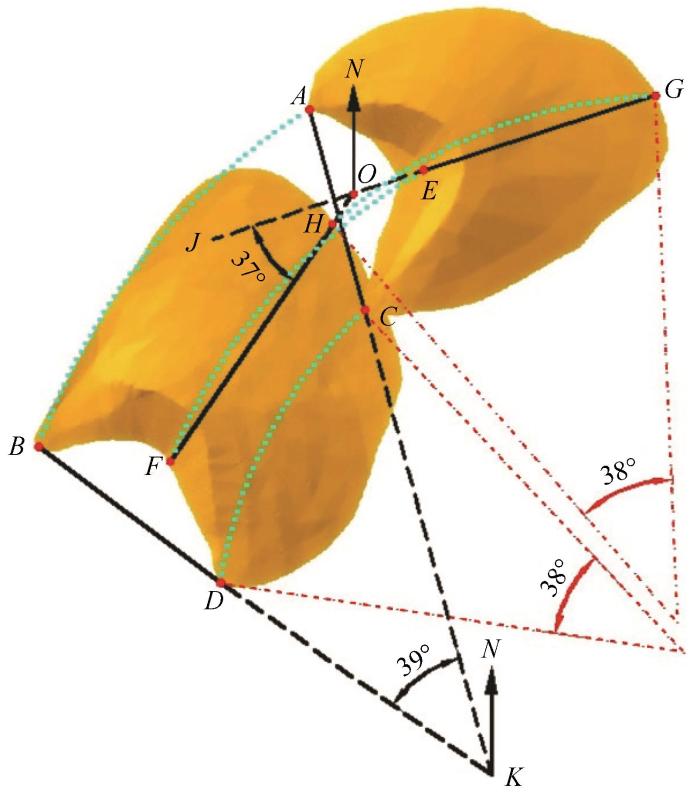
第1、2监测期间典型沙丘D3移动轨迹
Fig.6
Movement path for the typical barchan dune D3 between first and second monitoring period
在此监测期间,沙丘D3走向线由GE变为HF,走向线方位角由∠NOJ变为∠NOF,逆时针旋转变小约37°。两翼前端点连线由AC变为BD,两翼前端点连线方位角由∠NKA变为∠NKB,逆时针旋转变小约39°。沙丘D3特征点自NE向SW移动的同时,自身发生逆时针旋转。为使典型沙丘D3任意对应点旋转角度具有统一性,选取37°和39°的均值38°作为任意对应点的旋转角度值。将沙丘D3第1、2监测期任意两特征对应点为起点和端点,对应点旋转角度为夹角,利用AutoCAD 2010中起点、端点和夹角三要素拟合弧线的方法,实现沙丘对应特征点移动轨迹的拟合。
2.2.2 第2、3监测期间沙丘D3的移动轨迹拟合
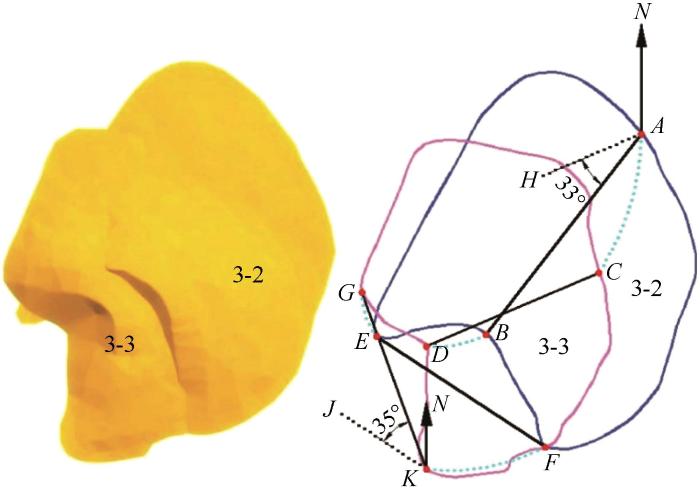
典型沙丘D3三维数字模型的叠加结果表明,第2、3监测期间,沙丘上特征点A移动到C,B移动到D, E移动到G,F移动到K(图7)。沙丘走向线由AB变为CD,走向线方位角由∠NAB变为∠NAH(AH∥CD),顺时针旋转变大约33°。两翼前端点连线由EF变为GK,两翼前端点连线方位角由∠NKJ变为∠NKG(EF∥JK),顺时针旋转变大约35°。为使沙丘D3上任意对应点旋转角度具有统一性,选取33°和35°的均值34°作为任意对应点的旋转角度。利用前述对应特征点移动轨迹的拟合方法,完成第2、3监测期间沙丘D3上对应特征点移动轨迹的拟合。
图7
图7
第2、3监测期间典型沙丘D3移动轨迹
Fig.7
Movement path for the typical barchan dunes D3 between second and third monitoring period
2.2.3 第3、4监测期间沙丘D3的移动轨迹拟合
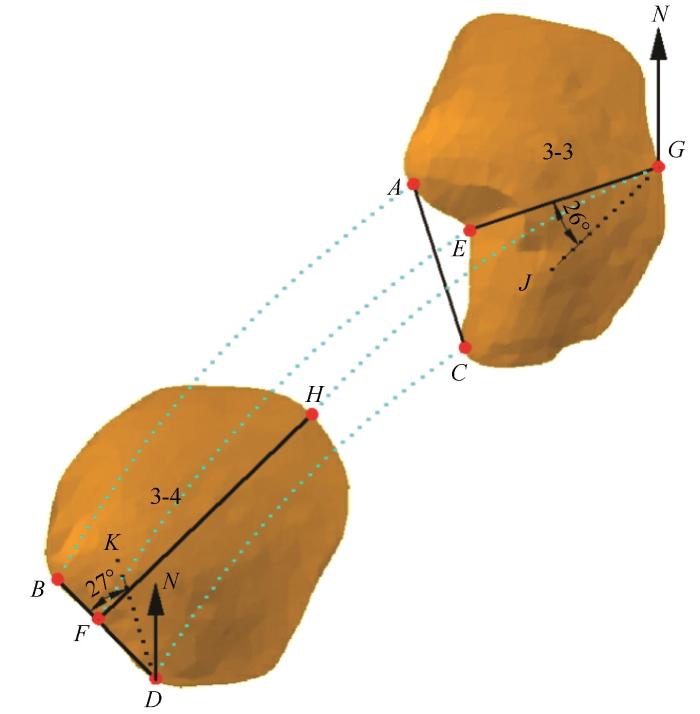
典型沙丘D3三维数字模型的叠加结果表明,第3、4监测期间,特征点A移动到B,C移动到D,G移动到H,E移动到F(图8)。沙丘走向线由GE变为HF,走向线方位角由∠NGE变为∠NGJ(GJ∥HF),逆时针旋转变小约26°。两翼前端点连线由AC变为BD,两翼前端点连线方位角由∠NDK变为∠NDB(DK∥AC),逆时针旋转变小约27°。为使沙丘D3上任意对应点旋转角度具有统一性,选取26°和27°的均值26.5°作为任意对应点的旋转角度。按照上述沙丘对应特征点移动轨迹的拟合方法,完成第3、4监测期间沙丘对应特征点移动轨迹的拟合。
图8
图8
第3、4监测期间典型沙丘D3移动轨迹
Fig.8
Movement path for the typical barchan dune D3 between third and fourth monitoring period
2.2.4 其他典型沙丘移动轨迹拟合
表1 7个典型沙丘相邻监测周期移动轨迹拟合特征
Table 1
| 监测期间 | 拟合轨迹特征 | 沙丘编号 | ||||||
|---|---|---|---|---|---|---|---|---|
| D1 | D2 | D4 | D5 | D6 | D7 | D8 | ||
| 第1、2 | 走向线旋转角度 | 32° | 35° | 35° | 36° | 32° | 32° | 33° |
| 翼端点连线旋转角度 | 34° | 37° | 36° | 40° | 35° | 39° | 36° | |
| 沙丘旋转角度 | 33° | 36° | 35.5° | 38° | 33.5° | 35.5° | 34. 5° | |
| 沙丘旋转方向 | 逆时针 | 逆时针 | 逆时针 | 逆时针 | 逆时针 | 逆时针 | 逆时针 | |
| 第2、3 | 走向线旋转角度 | 35° | 34° | 35° | 35° | 32° | 32° | 33° |
| 翼端点连线旋转角度 | 36° | 37° | 39° | 34° | 34° | 30° | 34° | |
| 沙丘旋转角度 | 35. 5° | 35.5° | 37° | 34.5° | 33° | 31° | 33. 5° | |
| 沙丘旋转方向 | 顺时针 | 顺时针 | 顺时针 | 顺时针 | 顺时针 | 顺时针 | 顺时针 | |
| 第3、4 | 走向线旋转角度 | 31° | 28° | 25° | 28° | 25° | 24° | 24° |
| 翼端点连线旋转角度 | 29° | 30° | 29° | 30° | 30° | 29° | 27° | |
| 沙丘旋转角度 | 30° | 29° | 27° | 29° | 25.5° | 26.5° | 25.5° | |
| 沙丘旋转方向 | 逆时针 | 逆时针 | 逆时针 | 逆时针 | 逆时针 | 逆时针 | 逆时针 | |
3 沙丘移动轨迹拟合结果和影响因素
3.1 沙丘移动轨迹拟合结果
在第1、2和第3、4监测期间,沙丘表面对应特征点均发生逆时针旋转,而在第2、3监测期间,对应特征点发生顺时针旋转。如沙丘移动轨迹为直线,沙丘的前移应是在直线运动轨迹上的位置改变,自身不会发生旋转。沙丘自身旋转角度的出现,说明沙丘移动轨迹应为曲线而非直线,拟合结果与沙丘实际移动轨迹更为吻合。
3.2 沙丘移动轨迹影响因素
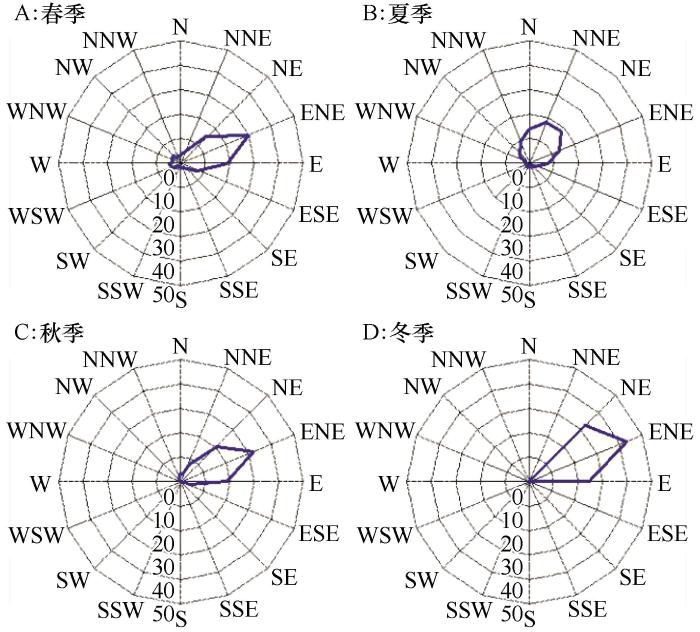
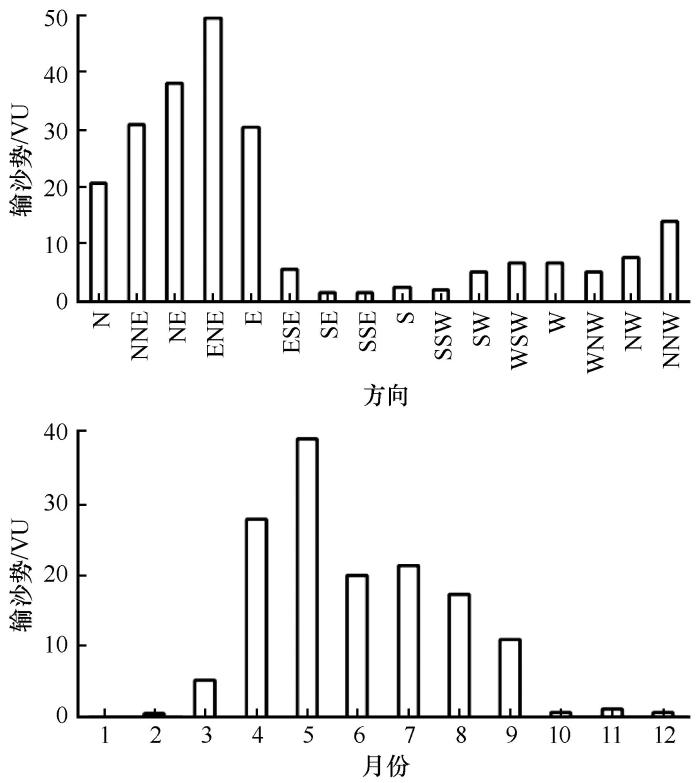
沙丘自NE向SW移动的同时,自身不断顺时针或逆时针旋转,使其移动轨迹为曲线而非直线。风况是引起新月形沙丘移动的动力因素[7],沙丘移动的总进程与测区四季ENE、NE和E向主起沙风的下风向一致[14-15](图9)。第1、2和第3、4监测期间分别为5—9月和4—9月,测区以春、秋和夏季为主。春、秋季测区以ENE、NE和E向起沙风为主,而夏季ENE、NE及E方向起沙风所占频率较大,且N、NNE及NNW方向起沙风所占频率亦高达41.3%。当夏季NNE、N和NNW向有效起沙风与沙丘轴向线的偏角大于30°时,沙丘迎风坡的NE侧成为迎风前坡,沙子受吹扬产生强烈吹蚀作用;沙丘SW侧成为迎风后坡,不断堆积从迎风前坡搬运来的沙粒,落沙坡侧向搬运现象和沙丘表面侵蚀堆积格局改变,沙丘自身出现逆时针旋转。测区NNW-E向有效起沙风的年均输沙势总和约为189VU,占全年80%以上,5—9月和4—9月的年均合成输沙势分别约占全年的80%和92%(图10)。因此,第1、2和第3、4监测期间有效起沙风频率较高且风速较大,输沙能力较强,风沙活动频繁,沙丘沿自NE指向SW且凸向NW的轨迹曲线快速前移。
图9
图10
第2、3监测期间为11月至翌年2月,测区以ENE、NE和E向的有效起沙风为主。当E和ENE向有效起沙风与沙丘轴向线的偏角大于30°时,沙丘迎风坡的SE侧成为迎风前坡,沙粒受吹扬产生强烈的吹蚀作用;沙丘NW侧成为迎风后坡,不断堆积从迎风前坡搬运来的沙粒,使沙丘自身出现顺时针旋转。但由于ENE、NE和E向的冬季有效起沙风频率较小且合成输沙势占全年的比例不足1%(图10),使沙丘在第2、3监测期间移动速度缓慢,仅沿自NE指向SW且凸向SE或SW向的轨迹曲线缓慢前移。
4 讨论
以沙丘移动直线轨迹为基础,已有研究表明,新月形沙丘的移动速度与沙丘高度成反比,而与风沙流输沙量成正比。用数理统计方法亦求得沙丘移动速度与沙丘高度间存有相关系数为0.8的负线性相关性,函数式为y=14.03-0.64h(y为移动速度(m·a-1),h为沙丘高度(m))。但按照前人研究所得的函数关系进行计算时,沙丘移动速度的计算值与实测值有较大差异[4,6],表明沙丘移动轨迹还需做进一步深入研究,且已有的移动速度计算公式也需进一步改进和完善。此外,已有研究表明,沙丘的移动方向为不同测量期沙丘前后位置对应点直线连线的方向且指向合成风向的下风向,不同点在直线移动轨迹上不同位置的移动方向相同[32]。而本研究结果表明,新月形沙丘前移动的同时自身出现逆时针或顺时针旋转,其移动轨迹为曲线而非直线,故沙丘某点的移动方向应为该点在轨迹曲线上的切线方向且指向合成风向的下风向,同一点在轨迹曲线不同位置的移动方向不同。
本项研究尝试了一种新月形沙丘三维数字模型建立和移动轨迹拟合的方法,其合理和科学性还有待进一步验证。但测区三维数字模型的建立,可为单期和多期流动性沙丘测量数据进行三维数字建模和移动轨迹拟合提供更好的技术支持,也为增强流动性沙丘显示的实时性奠定基础。本项研究中的等高距设置、TIN建立、栅格单元大小设置及其他相关参数的设置,选择三维可视化应用程序ArcScene 10进行三维数字建模,只适用于小范围高精度地形模拟,大范围区域的三维数字建模和移动轨迹拟合方法、参数设置以及建模和轨迹拟合软件选择等问题,还有待做进一步探索。
5 结论
本项研究以在新月形沙丘演变监测区测量的高精度三维坐标数据为一手研究数据,应用CASS 9.0和ArcGIS 10.0建立沙丘的三维数字模型并对相邻监测期的三维数字模型进行叠加,并利用Auto CAD 2010中起点、端点和夹角三要素拟合曲线的方法,对沙丘对应特征点的移动轨迹曲线进行了拟合。拟合结果表明,第1、2和第3、4监测期间,典型沙丘表面对应特征点移动轨迹曲线自NE指向SW且凸向NW,且呈平行状态,长度较大,移动速度较快。此外,沙丘对应特征点前移的同时发生逆时针旋转,旋转角度为33°~38°或25.5°~30°。第2、3监测期间,沙丘表面对应特征点移动轨迹曲线较为凌乱,凸向SE或SW,方向不一,长度较小。期间,沙丘对应特征点前移的同时发生顺时针旋转,旋转角度为31°~37°。
第1、2和第3、4监测期间,为风沙活动频繁的春、秋季和夏季,有效起沙风以输沙能力较强的NNW-E向风为主,沙丘自NE向SW快速前移。而第2、3监测期间,ENE、NE和E向有效起沙风风频较小,输沙能力较弱,沙丘移动缓慢。第1、2和第3、4监测期间,NNE、N和NNW向有效起沙风与沙丘轴向线的偏角大于30°,沙丘迎风坡的NE侧成为迎风前坡,沙丘SW侧成为迎风后坡;第2、3监测期间,E和ENE向有效起沙风与沙丘轴向线的偏角大于30°,沙丘迎风坡的SE侧成为迎风前坡,沙丘NW侧成为迎风后坡。沙丘迎风前坡不断受吹扬产生强烈吹蚀作用,而迎风后坡不断堆积从迎风前坡搬运来的沙子,落沙坡侧向搬运现象和沙丘表面侵蚀堆积格局改变,使沙丘发生逆时针或顺时针旋转。
沙丘自身旋转角度的出现,表明沙丘移动轨迹应为曲线而非直线。如沙丘移动轨迹为直线,沙丘的前移应是在直线运动轨迹上的位置改变,自身不会发生旋转,本项研究移动轨迹的曲线拟合结果与沙丘实际移动轨迹更为吻合。
参考文献
Barchan dune asymmetry:observations from Mars and Earth
[J].
Monitoring sand dune advance in the Taklimakan Desert
[J].
Aeolian dune field self-organization-implications for the formation of simple versus complex dune-field patterns
[J].
On the crescentic shape of barchan dunes
[J].
基于多旋翼无人机倾斜摄影测量的沙丘三维形态研究
[J].
植被盖度对风沙流结构及输沙率的影响
[J].
海岸新月形沙丘移动与形态变化的典型研究
[J].
A method for building 3D models of barchan dunes
[J].
Initiation and early development of barchan dunes:a case study of the Moroccan Atlantic Sahara desert
[J].
Wind velocity and sand transport on a barchan dune
[J].
巴丹吉林沙漠与腾格里沙漠连接带沙丘移动规律
[J].
Digital terrain analysis based on DEM
[J].
The research on the method of 3D terrain generation based on the digital terrain map
[J].
Study on generation technique of high quality contour lines based on grid DEM
[J].
Research and application on integration modeling of 3D bodies coal mine with blended data model based on TIN and ARTP
[J].
Based on Delaunay triangulation DEM of terrain model
[J].
Modeling screening efficiency with vibrational parameters based on DEM 3D simulation
[J].
Experiment study and regression analysis of molten pool in laser welding
[J].
0统计分析应用教程
[M].
The provenance and history of Abu Muharak barchan sands (Kharga Depression) inferred from textural,mineralogical,and geochemical perspectives
[J].





 甘公网安备 62010202000688号
甘公网安备 62010202000688号