0 引言
随着能源需求的增加,清洁且丰富的风能得到广泛关注[1 ] 。但是风具有间歇性和变异性,导致风电呈现出不稳定性[2 ] 。风电的不稳定性给风能管理和电力系统稳定运行提出了巨大挑战,这是造成风电并网困难、利用率低的主要原因之一[3 ] 。风电规划和风电预测预报能有效减小这一问题影响[4 ] ,准确的风速预报是提高风电利用率的最有效方式之一[5 ] 。
国内外学者提出了多种模型进行风速预测预报,主要分为物理模型和统计模型。物理模型基于物质、能量平衡和空气动力学机理,考虑温度、气压、地形等物理参数进行大空间、长时间风速预测,代表方法有数值天气预报等[6 ] 。但物理过程复杂,物理模型所需参数多,且需要长期稳定的气象资料作为驱动数据[7 ] ,不适用于风电场所需要的短期小区域风速预报[8 ] 。统计模型主要使用历史风速,通过建立数据间的映射关系实现风速预报。统计模型原理简单,计算量小,适应范围广,具有强大的非线性映射、泛化和自我学习能力。统计模型包括自回归时间序列模型,支持向量机、人工神经网络、极限学习机、卷积神经网络、长短时记忆网络等机器及深度学习模型。这些方法已经被应用于风速预报[9 -14 ] 。
但单独使用上述模型时预报精度并不理想,需要结合信号分解方法形成混合模型以提高预报精度[15 ] 。信号分解方法包括小波分解(Wavelet Decomposition,WD)、小波包分解(Wavelet Packet Decomposition,WPD)、经验模式分解(Empirical Mode Decomposition,EMD)及其改进方法等[16 ] 。小波分解可将复杂的原始信号分解为高频信号和低频信号,但该方法仅对信号低频部分详细分解,忽略了信号的高频部分,所以小波分解不适用于包含大量高频信息的信号(如风速)[17 ] ;经验模式分解及其改进方法虽然计算简单,但数学解释不明确[18 ] ,且有残余子信号(噪声);小波包分解数学解释明确,能够自行设定分解层数和分解使用的小波函数,已被广泛应用在风速预报中[19 -21 ] 。
目前,大量研究通过改进已有模型[1 ] 、应用新方法[22 ] 以及耦合不同信号分解方法[23 ] 等来提高模型预报精度。随着深度学习方法快速发展,在混合模型中加入深度学习模型进行风速预报的研究日益增多。但这些模型预报机理差异大,多种单一模型或与信号分解方法耦合形成的混合模型之间的差异性对比研究不足。
鉴于此,本研究通过对比多种统计模型以及这些模型与小波包分解耦合模型在预报3种下垫面风速的表现,探索较好的风速预报模型。研究结果可为不同下垫面风速预报模型的选择与优化提供参考,为风电场准确预报风速,保证稳定供电提供理论支持。
1 研究方法与数据
1.1 基础预报模型
基于最新文献研究,本研究选取广泛应用的12种机器学习和深度学习模型。
1.1.1 支持向量回归
支持向量回归属于支持向量机,主要应用于回归问题。其核心思想是寻找一条最佳拟合曲线,在容忍偏差范围内,曲线包含尽可能多的数据点。回归方程的数学描述为[24 ] :
f ( x ) = w T φ ( x ) + b (1)
m i n w , b , ξ , ξ * 1 2 w T w + C ∑ i = 1 n ( ξ i + ξ i * ) (2)
s . t . y i - < w , x i > + b ≤ ε + ξ i < w , x i > + b - y i ≤ ε + ξ i * ( i = 1,2 , … , l ) ξ i , ξ i * ≥ 0 (3)
式中:l 为样本数;xi 和yi 分别为训练集的输入和输出数据;n 为总样本数;ξ 和ξ * 分别为训练误差上界和下界;ε 为不敏感损失因子;C 为正则常量。
f x , a i , a i * = ∑ i = 1 n a i - a i * K x , x i + b (4)
式中:f (x , a i , a i * a 为拉格朗日乘数;a * 为拉尔朗日乘数;K (x,xi )为核函数。
1.1.2 梯度提升回归
梯度提升回归是一种集成学习算法[25 ] ,该算法基于分类回归树(Classification and regression tree, CART)和序列提升算法构建。算法目的是最小化损失函数,减小残差。为实现此目的,首先计算初始模型残差,在梯度下降方向使用残差拟合基础学习器,再使用拟合后的基础学习器更新模型,不断重复上述过程获得目标模型。
1.1.3 随机森林
随机森林也是一种基于分类回归树构建的集成学习算法,它基于装袋算法实现。随机森林在训练时,先从原始数据中有放回、平均地抽取多个子数据集,在子数据集上拟合分类回归树,最终结果由所有树结果的平均值决定,所有分类回归树构成随机森林模型。装袋算法和分类回归树构建过程中都存在随机性,可有效避免随机森林过拟合。
1.1.4 人工神经网络
人工神经网络受人类大脑结构启发得到,由一系列相互连接的神经元构成。网络内部不同神经元之间通过权重相连,神经元内设有激活函数和偏差。根据激活函数和学习算法的不同,人工神经网络可以分为不同类别。其数学描述为[25 ] :
y i ( n ) = f ∑ j = 1 N w i j ( n , n - 1 ) y j n - 1 + θ i n (5)
式中:i 为第n 层的神经元;wij 为第n- 1层神经元j 和第n 层神经元i 之间的权重;θi n 为第n -t 层神经元i 的偏差。
1.1.5 极限学习机
极限学习机是一类包含单个隐藏层的前馈神经网络[26 ] ,该算法的最大特点是保证学习精度的前提下训练速度更快。极限学习机在训练模型前,首先随机初始化输入权重和偏差,同时确定输出矩阵。不同于传统神经网络,极限学习机在迭代时不需要更新全部参数,仅通过输出矩阵求解相应方程组就能快速训练模型。其损失函数描述为[27 ] :
E = ∑ j = 1 N ∑ i = 1 L β i g w i x j + b i - t j 2 (6)
式中:N L β i g · w i x j b i t j
1.1.6 卷积神经网络
卷积神经网络能够提取数据特征,在处理时间序列数据方面有良好表现。相较于支持向量机和人工神经网络等浅层模型,卷积神经网络模型特有的卷积层可以实现自动特征选取,其全连接层处理有短期依赖的高频子集能力强[28 ] 。卷积层内,各个神经元间无相互联系,只共享卷积核权重。相较于人工神经网络,该模型训练更有效。每个卷积层的数学描述为[29 ] :
h i j k = f ( ( w k x ) i j + b k ) (7)
式中:f 为激活函数;wk 为卷积核连接到第k 个特征图的权重。
1.1.7 循环神经网络
循环神经网络是一种处理时间序列数据的方法,但传统循环神经网络训练过程中常出现梯度消失或梯度爆炸问题。为解决此问题,提出了长短时记忆网络[30 ] ,该方法能有效处理长短期依赖问题。长短时记忆网络的核心组件为输入门、遗忘门和输出门。输入门决定细胞状态中存储的信息,遗忘门决定被遗忘的信息,输出门决定最终输出。单个神经元计算过程为:①输入数据,输入门激活,计算输入细胞信息;②如果遗忘门激活,遗忘部分细胞中保留的历史状态;③输出门激活,计算输出信息。神经元内计算过程可以描述为[28 ] :
i t = σ ( w i x x t + w i m m t - 1 + w i c c t - 1 + b i ) (8)
f t = σ ( w f x x t + w f m m t - 1 + w f c c t - 1 + b f ) (9)
c t = f ° c t - 1 + i t ° t a n h ( w c x x t + w c m m t - 1 + b c ) (10)
o t = σ ( w o x x t + w o m m t - 1 + w o c c t - 1 + b o ) (11)
m t = o t ° t a n h ( c t ) (12)
y t = w y m m t + b y (13)
式中:x =(x 1 , x 2 , x 3 ,…,xT )为展开层数据;it 为输入门;ft 为遗忘门;ct 为记忆细胞的激活矢量;ot 为输出门;mt 为每个记忆块的激活矢量;w 为权重矩阵;b 为偏差矢量;°为点积;σ 和tanh 为激活函数,激活函数数学描述为[28 ] :
σ ( x ) = 1 / ( 1 + e - x ) (14)
t a n h ( x ) = ( e x - e - x ) / ( e x + e - x ) (15)
在长短时记忆网络发展中出现了许多变种模型,如双向长短时记忆网络、门控循环单元等。其中,双向长短时记忆网络利用历史信息和未来信息进行预报,门控循环单元减少了门的数量,模型原理与长短时记忆网络相似。此外,还有堆叠式长短时记忆网络、卷积长短时记忆网络和卷积门控循环单元等模型。
1.2 小波包分解
小波包分解源于小波分解,它在分解信号低频子集同时,对高频子集继续分解。因此,该方法适用于分解含有大量高频信息的风速信号,以获取更加准确的信息。小波包分解使用时仅需要设置小波函数和分解层数。根据分解的信号类别,小波包分解可分为离散小波转换和连续小波转换。由于风速的连续性,本研究使用连续小波转换,数学描述为[31 ] :
C W T a , b = 1 a ∫ - ∞ ∞ x ( t ) Ψ * t - b a d t (16)
式中:x (t )为原始信号;Ψ * 为母小波函数;a 为比例因子;b 为转换参数;*为共轭复数;t 为原始信号对应的时间点。
1.3 信号分解与基础预报模型耦合设计
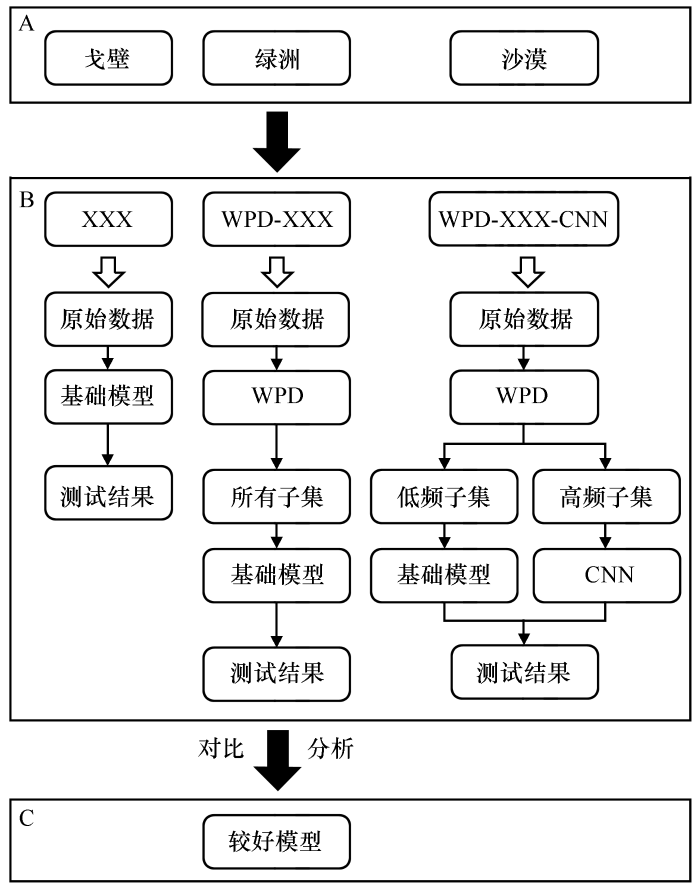
根据已有文献,常用混合模型大多为信号分解方法和基础预报模型组成。由于信号分解子集各有特点,一些混合模型仅使用一种基础预报模型预报所有子集[30 ] ,另一些模型针对不同频率子集使用不同模型进行预报[28 ] 。本实验方案为:①选择应用广泛的机器学习和最新的深度学习模型共12个作为基础预报模型(简称单一XXX模型,表1 ),研究各种单一模型在风速预报中的表现;②小波包分解与12个基础预报模型耦合(简称WPD-XXX混合模型),探索小波包分解在提高模型预报精度中的作用;③小波包分解与12个基础预报模型和卷积神经网络(CNN)耦合(简称WPD-XXX-CNN混合模型),这里CNN用于预报小波包分解子集中的高频子集,而12个单一XXX模型用于预报低频子集。单一XXX模型作为对照组,WPD-XXX混合模型和WPD-XXX-CNN混合模型为实验组。单一XXX模型对照组中,使用12个基础预报模型直接预报风速;WPD-XXX实验组中,先将风速分解为低频和高频子集,再由XXX模型分别预报所有子集,最后将子集预报结果相加得出最终预报结果;WPD-XXX-CNN实验组中,利用卷积神经网络模型预报高频子集,XXX模型预报低频子集,最后将子集预报结果相加,得到最终结果。算法流程见图1 。
图1
图1
算法流程图(A为3种下垫面,B为3种模型结构,C为较好模型)
Fig.1
Algorithm flowchart (A indicates the dataset, B indicates three kinds of models, C indicates the optimized models)
1.4 数据应用和评价指标
1.4.1 原始数据与重构
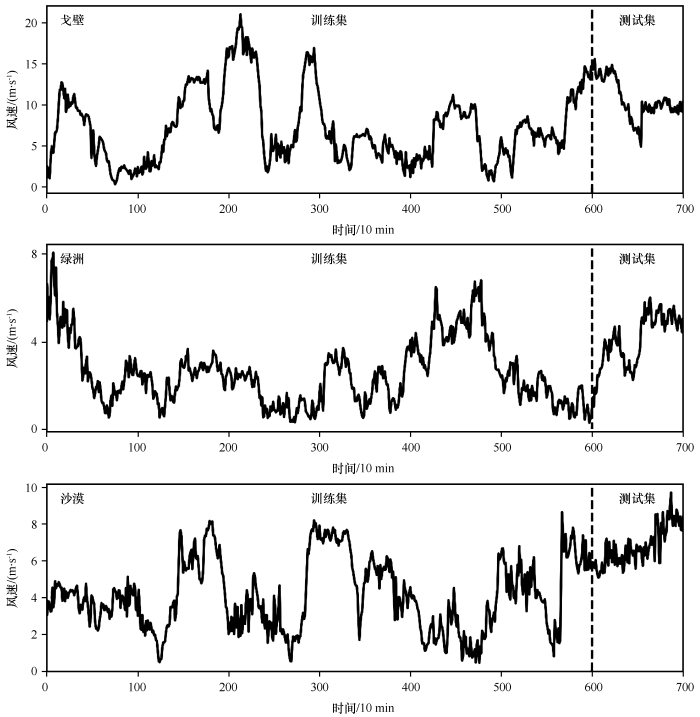
数据源于中国西北地区3个野外试验观测点,下垫面分别为戈壁、绿洲和沙漠(表2 )。风速时间序列见图2 。
图2
图2
3种下垫面风速时间序列
Fig.2
Wind speed time series
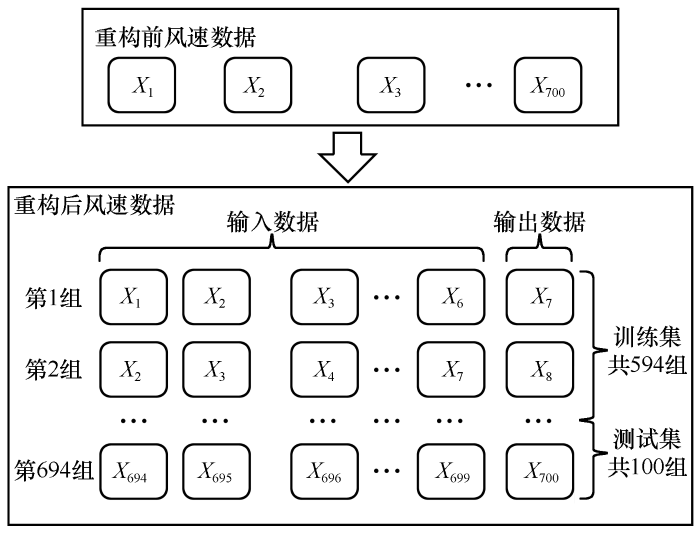
基于现有研究的数据组织方式[32 ] ,本研究风速数据重构过程如图3 。选择6个历史数据作为输入数据,数据重构时,每次选取7个数据为一组样本,平移1个位置选取下一组样本。因此,前后两组样本数据中有6个相同数据。最终得到694组样本数据,并以594∶100的比例划分为训练集和测试集。数据重构前进行最大最小值标准化,公式为:
x 2 = ( x 1 - x m i n ) / ( x m a x - x m i n ) (17)
式中:x 1 和x 2 分别为标准化前和标准化后风速;x max 和x min 分别为标准化前最大和最小风速。
图3
图3
数据重构示意图
Fig.3
Schematic diagram of data reconstruction
1.4.2 精度指标
为了对比分析模型预报精度,本研究使用3种精度指标:平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)、平均绝对误差(Mean Absolute Error, MAE)和均方根误差(Root Mean Square Error, RMSE)[33 ] 。
M A P E = ∑ t = 1 n x t - x ̂ t x t / N (18)
M A E = ∑ t = 1 n x t - x ̂ t / N (19)
R M S E = ∑ t = 1 n ( x ( t ) - x ̂ ( t ) ) 2 / N (20)
式中:x (t )为原始风速;x ̂ t n 为样本数。
2 结果
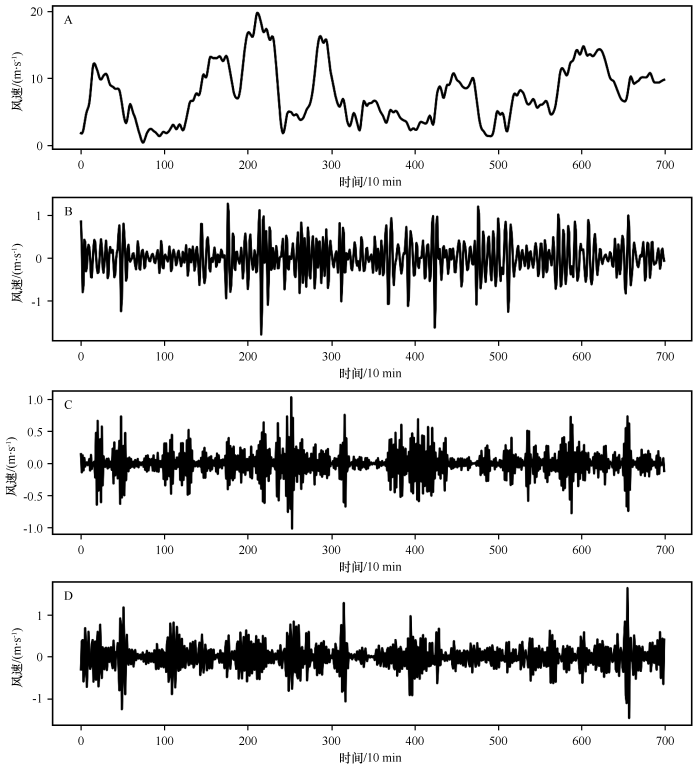
为了对比分析信号分解方法与不同基础预报模型耦合之间的差异,首先将原始风速数据分解为1个低频子集(图4 A)和3个高频子集(图4 B—D)。在对模型进行对比分析时,加入多模型平均方法,探讨其对模型结果的影响,多模型平均方法采用12个模型平均(简称A12)和3个较好模型平均(简称A3)。
图4
图4
数据集分解子集(以戈壁下垫面为例,A为低频子集,B、C、D为高频子集)
Fig.4
The sub-layers of the gobi dataset (A is the low-frequency sub-layer; B, C, D are the high-frequency sub-layers,perspectively)
2.1 3 种模型在不同下垫面的预报精度
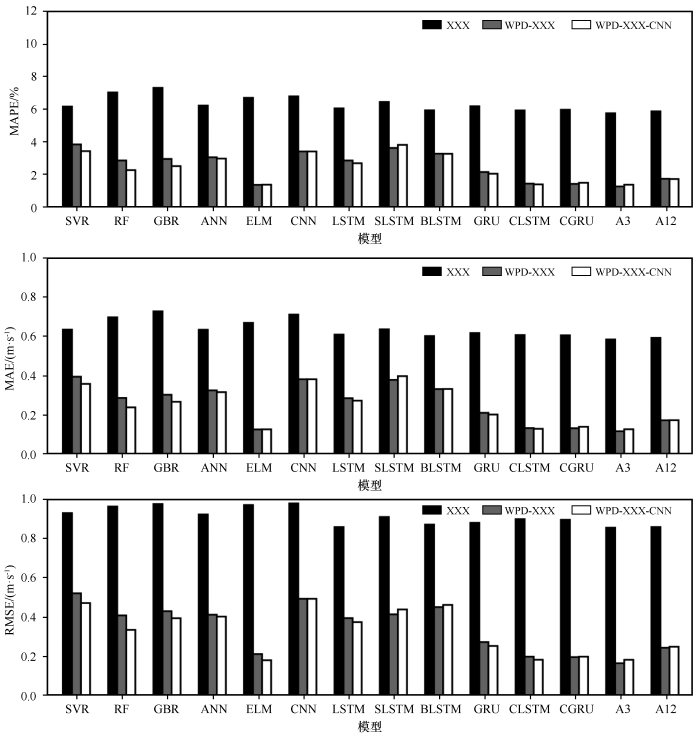
模型预报能力在3个下垫面相似(图5 —7 ),下面以戈壁下垫面的预报结果为例说明。
图5
图5
戈壁下垫面3种模型预报精度
A3为3个较好模型平均值,A12为12个模型平均值
Fig.5
The forecast accuracy of three kinds of models in gobi (A3 is the average of three better models, and A12 is the average of all the 12 models)
图6
图6
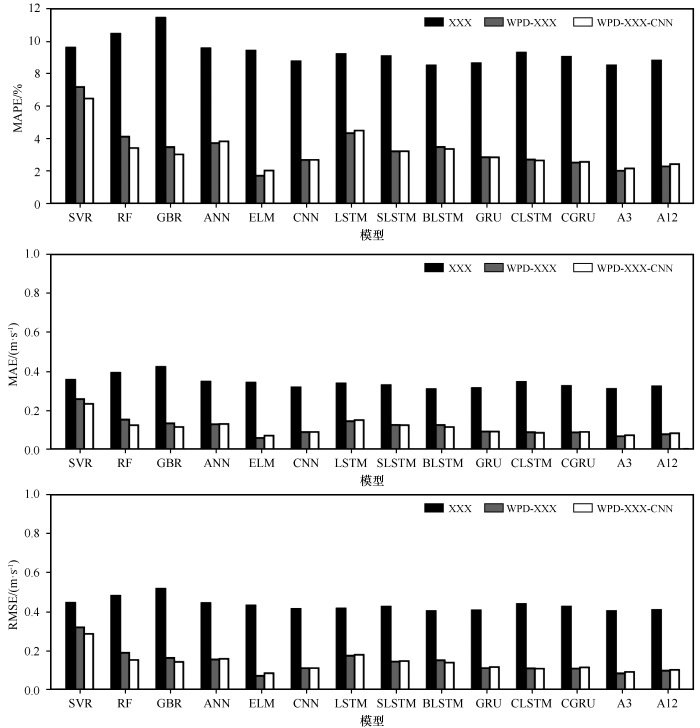
绿洲下垫面3种模型预报精度
A3为3个较好模型平均值,A12为12个模型平均值
Fig.6
The forecast accuracy of three kinds of models in oasis (A3 is the average of three better models, and A12 is the average of all the 12 models)
图7
图7
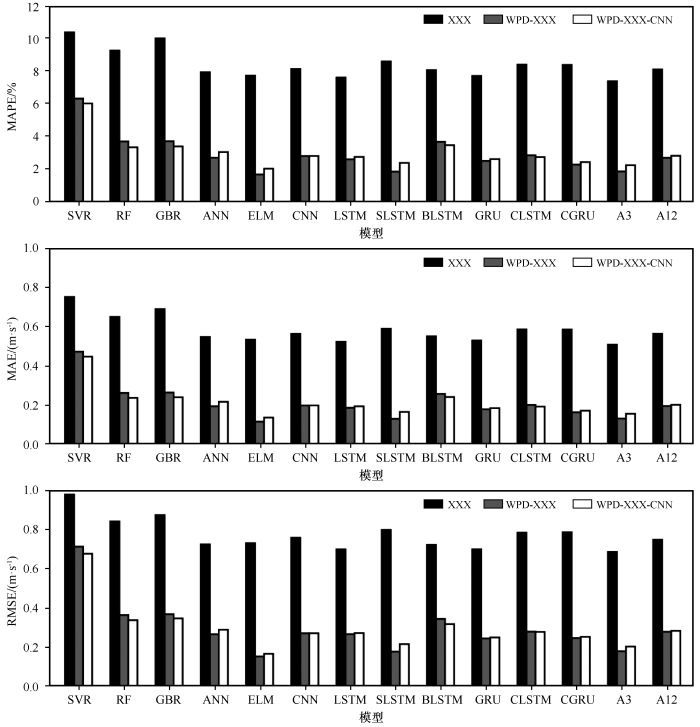
沙漠下垫面3种模型预报精度
A3为3个较好模型平均值,A12为12个模型平均值
Fig.7
The forecast accuracy of three kinds of models in desert (A3 is the average of three better models, and A12 is the average of all the12 models)
小波包分解显著提高了单一模型精度。以SVR模型为例,WPD-SVR模型误差(MAPE为3.81%,MAE为0.40 m·s-1 ,RMSE为0.52 m·s-1 )远低于SVR模型的误差(MAPE为6.13%,MAE为0.64 m·s-1 ,RMSE为0.93 m·s-1 ),WPD-SVR模型相较于SVR模型精度显著提高。其余11个模型规律相同。该结果证明小波包分解能够显著提高单一XXX模型的预报精度。
利用卷积神经网络模型来预报高频子集,对多数WPD-XXX混合模型的预报精度影响不明显。以WPD-SVR模型为例,WPD-SVR-CNN模型误差(MAPE为3.40%,MAE为0.36 m·s-1 ,RMSE为0.47 m·s-1 )低于WPD-SVR模型误差(MAPE为3.81%,MAE为0.40 m·s-1 ,RMSE为0.52 m·s-1 ),WPD-SVR-CNN模型精度较好,卷积神经网络小幅度提高了WPD-SVR模型精度。但是对于WPD-SLSTM模型,WPD-SLSTM-CNN模型误差值(MAPE为3.78%,MAE为0.40 m·s-1 ,RMSE为0.44 m·s-1 )全都大于WPD-SLSTM模型(MAPE为3.59%,MAE为0.38 m·s-1 ,RMSE为0.41 m·s-1 ),WPD-SLSTM模型精度好,卷积神经网络没有提高WPD-SLSTM模型精度。戈壁数据集WPD-ELM-CNN模型精度略微高于WPD-ELM模型。加入卷积神经网络模型后,总计8个模型精度小幅度提高,3个模型精度未提高。该结果说明,卷积神经网络对提高WPD-XXX混合模型的精度有限。
这些模型中,小波包分解和极限学习机的耦合(WPD-ELM)、小波包分解和集特征提取和记忆功能的卷积长短时记忆网络(CLSTM)和卷积门控循环单元(CGRU)模型耦合具有较好的预报能力。其中,WPD-ELM模型误差值(MAPE为1.33%,MAE为0.13 m·s-1 ,RMSE为0.21 m·s-1 )、WPD-CLSTM模型误差值(MAPE为1.40%,MAE为0.13 m·s-1 ,RMSE为0.20 m·s-1 )和WPD-CGRU模型误差值(MAPE为1.39%,MAE为0.13 m·s-1 ,RMSE为0.19 m·s-1 )相对较低,在3组模型中精度较好。
WPD-XXX混合模型中3个较好模型平均值精度较好。在WPD-XXX混合模型实验组中,3个较好模型误差值(MAPE为1.23%,MAE为0.12 m·s-1 ,RMSE为0.16 m·s-1 )小于WPD-ELM模型误差值(MAPE为1.33%,MAE为0.13 m·s-1 ,RMSE为0.21 m·s-1 ),3个较好模型平均值精度优于WPD-ELM模型精度。在其他WPD-XXX模型中,WPD-ELM模型精度相对较好,故而,在WPD-XXX混合模型中,3个较好模型精度较好,能够提高模型精度。
2.2 3 种模型预报结果拟合程度
对于3种下垫面,3种模型预报结果的拟合程度相似(表3 ),在此仅以戈壁下垫面进行说明。
小波包分解显著提高单一模型预报结果的拟合程度。以SVR模型为例,单一XXX模型中SVR模型R 2 R 2 R 2
卷积神经网络模型对所有WPD-XXX混合模型预报拟合程度提高不显著。以WPD-SVR模型为例, WPD-SVR模型R 2 R 2 R 2 R 2 R 2 R 2
这3组实验中,小波包分解和卷积长短时记忆网络以及卷积门控循环单元的耦合模型拟合程度相对较好。WPD-ELM模型R 2 R 2 R 2 R 2
对于戈壁下垫面,单一XXX模型和WPD-XXX混合模型实验组中,3个较好模型拟合程度优于其余模型拟合程度。单一XXX模型中,3个较好模型R 2
2.3 多模型预报结果不稳定性
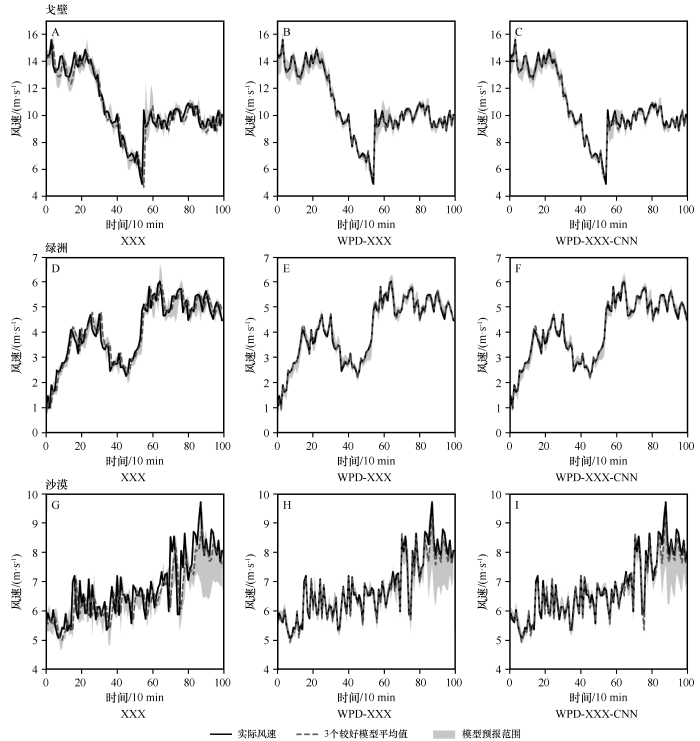
由图8 可见:3个较好模型平均的预报曲线与实际观测值接近,多模型平均避免了单个模型在某些点上具有较大误差,如局部极值点处。模型预报范围(即阴影范围)较大,平均值的使用使预报结果更接近实际观测值。同时,图8 也体现了小波包分解对模型整体精度的提高(图8 中阴影范围明显减小)。值得注意的是,沙漠下垫面模型预报结果很不稳定。
图8
图8
3种下垫面3种模型预报结果
Fig.8
The forecast results of three kinds of models in three datasets
3 讨论
本研究中,小波包分解和卷积长短时记忆网络以及卷积门控循环单元的耦合模型在不同数据集上都表现较好。对于戈壁下垫面,WPD-ELM模型MAPE值为1.33%,WPD-CLSTM模型MAPE值为1.40%,WPD-CGRU模型MAPE值为1.39%。相较于文献[2 ](5.638%)和文献[9 ](8.92%),本研究中模型MAPE值较小,模型预报精度更好。其余下垫面预报结果相似。这表明本研究采用的小波包分解与深度学习模型的耦合模型对风速有较好的预报能力。
(1) 信号分解能有效降低数据复杂性,机器学习模型对分解后的风速信号预报能力更强。原始风速具有间歇性和不稳定性,信号复杂,机器学习模型对其预报能力差。但信号分解方法可将复杂的原始信号转换为更加稳定的分量,降低了原始风速内在特性的影响,机器学习模型对各稳定分量的预报精度更高,因此,单一XXX模型与小波包分解组成的混合模型对风速的预报能力大大增强。这与Zhang等[33 ] 的研究结果一致。
(2) 深度学习模型对复杂时间序列预报能力更强。卷积长短时记忆网络和卷积门控循环单元既具有卷积神经网络的自动特征选择功能,又具有循环神经网络的记忆功能。ELM为单个隐藏层前馈神经网络,模型结构简单,训练速度快,不需要复杂的参数选择就能快速学习数据的内部规律。Hao等[34 ] 使用极限学习机预报风速分量以及风速误差序列,Ghimire等[35 ] 在深度太阳辐射预报中使用卷积长短时记忆网络,Liu等[36 ] 使用卷积门控循环单元预报风速序列子集,都有着相似发现。
(3) 不同模型具有不同学习能力,本研究中主要体现在极值预报上。在极值点处单一模型预报误差较大,而多模型平均使得预报结果更加平滑,预报值更接近实际观测值。多模型平均能有效利用不同模型特点,在极值预报上实现互补。Feng等[25 ] 使用深度特征选择和多模型预报风速,模型预报精度明显优于单一模型。
4 结论
小波包分解可有效降低时间序列数据的复杂性,提高模型预报精度。
小波包分解与具有特征学习和记忆功能的深度学习模型(如卷积长短时记忆网络、卷积门控循环单元)的耦合具有较好的预报能力。
不同模型在时间序列风速不同时间点上预报能力不同,多个模型的集合预报(特别是较好模型集合如3个较好模型集合)可以取长补短,因此多个模型的集合预报有更好的结果。
参考文献
View Option
[1]
Liu M S Cao Z M Zhang J et al Short-term wind speed forecasting based on the Jaya-SVM model
[J].International Journal of Electrical Power & Energy Systems ,2020 ,121 :106056 .
[本文引用: 2]
[2]
王俊 ,李霞 ,周昔东 ,等 基于VMD和LSTM的超短期风速预测
[J].电力系统保护与控制 ,2020 ,48 (11 ):45 -52 .
[本文引用: 2]
[3]
张丽英 ,叶廷路 ,辛耀中 ,等 大规模风电接入电网的相关问题及措施
[J].中国电机工程学报 ,2010 ,30 (25 ):1 -9 .
[本文引用: 1]
[4]
Liu H Mi X W Li Y F Comparison of two new intelligent wind speed forecasting approaches based on wavelet packet decomposition,complete ensemble empirical mode decomposition with adaptive noise and artificial neural networks
[J].Energy Conversion and Management ,2018 ,155 :188 -200 .
[本文引用: 1]
[5]
Dong Q L Sun Y H Li P Z A novel forecasting model based on a hybrid processing strategy and an optimized local linear fuzzy neural network to make wind power forecasting:a case study of wind farms in China
[J].Renewable Energy ,2017 ,102 :241 -257 .
[本文引用: 1]
[6]
Howard T Clark P Correction and downscaling of NWP wind speed forecasts
[J].Meteorological Applications ,2007 ,14 (2 ):105 -116 .
[本文引用: 1]
[7]
黄彦辉 ,王龙杰 ,杨薛明 基于混沌时间序列的支持向量机短期风速预测模型研究
[J].电测与仪表 ,2015 ,52 (17 ):32 -37 .
[本文引用: 1]
[8]
李应求 ,安勃 ,李恒通 基于NARX及混沌支持向量机的短期风速预测
[J].电力系统保护与控制 ,2019 ,47 (23 ):65 -73 .
[本文引用: 1]
[9]
梁智 ,孙国强 ,俞娜燕 ,等 基于高斯过程回归和粒子滤波的短期风速预测
[J].太阳能学报 ,2020 ,41 (3 ):45 -51 .
[本文引用: 2]
[10]
喻敏 ,常毓婵 ,袁浩 ,等 基于HP-EMD和ARMA的短期风速预测
[J].中国科技论文 ,2016 ,11 (5 ):566 -570 .
[11]
孙驷洲 ,陈亮 ,郭兴众 ,等 基于EEMD与极限学习机的短期风速组合预测模型
[J].安徽工程大学学报 ,2018 ,33 (4 ):56 -63 .
[12]
王晨 ,寇鹏 基于卷积神经网络和简单循环单元集成模型的风电场内多风机风速预测
[J].电工技术学报 ,2020 :1 -14 .
[13]
Yu C J Li Y L Xiang H Y et al Data mining-assisted short-term wind speed forecasting by wavelet packet decomposition and elman neural network
[J].Journal of Wind Engineering and Industrial Aerodynamics ,2018 ,175 :136 -143 .
[14]
Harbola S Coors V One dimensional convolutional neural network architectures for wind prediction
[J].Energy Conversion and Management ,2019 ,195 :70 -75 .
[本文引用: 1]
[15]
Liu H Tian H Q Li Y F Four wind speed multi-step forecasting models using extreme learning machines and signal decomposing algorithms
[J].Energy Conversion and Management ,2015 ,100 :16 -22 .
[本文引用: 1]
[16]
Hao Y Tian C S A novel two-stage forecasting model based on error factor and ensemble method for multi-step wind power forecasting
[J].Applied Energy ,2019 ,238 :368 -383 .
[本文引用: 1]
[17]
Liu H Tian H Q Liang X F et al Wind speed forecasting approach using secondary decomposition algorithmn and elman neural networks
[J].Applied Energy ,2015 ,157 :183 -194 .
[本文引用: 1]
[18]
Pei S Q Qin H Zhang Z et al Wind speed prediction method based on empirical wavelet transform and new cell update long short-term memory network
[J].Energy Conversion and Management ,2019 ,196 :779 -792 .
[本文引用: 1]
[19]
叶瑞丽 ,郭志忠 ,刘瑞叶 ,等 基于小波包分解和改进Elman神经网络的风电场风速和风电功率预测
[J].电工技术学报 ,2017 ,32 (21 ):103 -111 .
[本文引用: 1]
[20]
王宁 ,罗汝斌 ,廖俊 ,等 基于小波包分解的BP神经网络的短期风速预测
[J].控制与信息技术 ,2019 (4 ):44 -49 .
[21]
Mi X W Liu H Li Y F Wind speed forecasting method using wavelet,extreme learning machine and outlier correction algorithm
[J].Energy Conversion and Management ,2017 ,151 :709 -722 .
[本文引用: 1]
[22]
Liu H Yu C Q Wu H P et al A new hybrid ensemble deep reinforcement learning model for wind speed short term forecasting
[J].Energy ,2020 ,202 :1 -36 .
[本文引用: 1]
[23]
Moreno S R Silva R G D Mariani V C et al Multi-step wind speed forecasting based on hybrid multi-stage decomposition model and long short-term memory neural network
[J].Energy Conversion and Management ,2020 ,213 :112869 .
[本文引用: 1]
[24]
Mi X W Liu H Li Y F Wind speed prediction model using singular spectrum analysis,empirical mode decomposition and convolutional support vector machine
[J].Energy Conversion and Management ,2019 ,180 :196 -205 .
[本文引用: 3]
[25]
Feng C Cui M J Hodge B M et al A data-driven multi-model methodology with deep feature selection for short-term wind forecasting
[J].Applied Energy ,2017 ,190 :1245 -1257 .
[本文引用: 3]
[26]
Liu H Mi X W Li Y F An experimental investigation of three new hybrid wind speed forecasting models using multi-decomposing strategy and ELM algorithm
[J].Renewable Energy ,2018 ,123 :694 -705 .
[本文引用: 1]
[27]
Liu H Mi X W Li Y F Smart multi-step deep learning model for wind speed forecasting based on variational mode decomposition,singular spectrum analysis,LSTM network and ELM
[J].Energy Conversion and Management ,2018 ,159 :54 -64 .
[本文引用: 1]
[28]
Liu H Mi X W Li Y F Smart deep learning based wind speed prediction model using wavelet packet decomposition,convolutional neural network and convolutional long short term memory network
[J].Energy Conversion and Management ,2018 ,166 :120 -131 .
[本文引用: 4]
[29]
Ding L Y Fang W L Luo H B et al A deep hybrid learning model to detect unsafe behavior:integrating convolution neural networks and long short-term memory
[J].Automation in Construction ,2018 ,86 :118 -124 .
[本文引用: 1]
[30]
Memarzadeh G Keynia F A new short-term wind speed forecasting method based on fine-tuned LSTM neural network and optimal input sets
[J].Energy Conversion and Management ,2020 ,213 :112824 .
[本文引用: 2]
[31]
Li Y F Shi H P Han F Z et al Smart wind speed forecasting approach using various boosting algorithms,big multi-step forecasting strategy
[J].Renewable Energy ,2019 ,135 :540 -553 .
[本文引用: 1]
[32]
Zhang Y G Pan G F Chen B et al Short-term wind speed prediction model based on GA-ANN improved by VMD
[J].Renewable Energy ,2020 ,156 :1373 -1388 .
[本文引用: 1]
[33]
Zhang J L Wei Y M Tan Z F An adaptive hybrid model for short term wind speed forecasting
[J].Energy ,2019 ,190 :115615 .
[本文引用: 2]
[34]
Hao Y Tian C A novel two-stage forecasting model based on error factor and ensemble method for multi-step wind power forecasting
[J].Applied Energy ,2019 ,238 :368 -383 .
[本文引用: 1]
[35]
Ghimire S Deo R C Raj N et al Deep solar radiation forecasting with convolutional neural network and long short-term memory network algorithms
[J].Applied Energy ,2019 ,253 :113541 .
[本文引用: 1]
[36]
Liu H Mi X W Li Y F et al Smart wind speed deep learning based multi-step forecasting model using singular spectrum analysis,convolutional gated recurrent unit network and support vector regression
[J].Renewable Energy ,2019 ,143 :842 -854 .
[本文引用: 1]
Short-term wind speed forecasting based on the Jaya-SVM model
2
2020
... 随着能源需求的增加,清洁且丰富的风能得到广泛关注[1 ] .但是风具有间歇性和变异性,导致风电呈现出不稳定性[2 ] .风电的不稳定性给风能管理和电力系统稳定运行提出了巨大挑战,这是造成风电并网困难、利用率低的主要原因之一[3 ] .风电规划和风电预测预报能有效减小这一问题影响[4 ] ,准确的风速预报是提高风电利用率的最有效方式之一[5 ] . ...
... 目前,大量研究通过改进已有模型[1 ] 、应用新方法[22 ] 以及耦合不同信号分解方法[23 ] 等来提高模型预报精度.随着深度学习方法快速发展,在混合模型中加入深度学习模型进行风速预报的研究日益增多.但这些模型预报机理差异大,多种单一模型或与信号分解方法耦合形成的混合模型之间的差异性对比研究不足. ...
基于VMD和LSTM的超短期风速预测
2
2020
... 随着能源需求的增加,清洁且丰富的风能得到广泛关注[1 ] .但是风具有间歇性和变异性,导致风电呈现出不稳定性[2 ] .风电的不稳定性给风能管理和电力系统稳定运行提出了巨大挑战,这是造成风电并网困难、利用率低的主要原因之一[3 ] .风电规划和风电预测预报能有效减小这一问题影响[4 ] ,准确的风速预报是提高风电利用率的最有效方式之一[5 ] . ...
... 本研究中,小波包分解和卷积长短时记忆网络以及卷积门控循环单元的耦合模型在不同数据集上都表现较好.对于戈壁下垫面,WPD-ELM模型MAPE值为1.33%,WPD-CLSTM模型MAPE值为1.40%,WPD-CGRU模型MAPE值为1.39%.相较于文献[2 ](5.638%)和文献[9 ](8.92%),本研究中模型MAPE值较小,模型预报精度更好.其余下垫面预报结果相似.这表明本研究采用的小波包分解与深度学习模型的耦合模型对风速有较好的预报能力. ...
大规模风电接入电网的相关问题及措施
1
2010
... 随着能源需求的增加,清洁且丰富的风能得到广泛关注[1 ] .但是风具有间歇性和变异性,导致风电呈现出不稳定性[2 ] .风电的不稳定性给风能管理和电力系统稳定运行提出了巨大挑战,这是造成风电并网困难、利用率低的主要原因之一[3 ] .风电规划和风电预测预报能有效减小这一问题影响[4 ] ,准确的风速预报是提高风电利用率的最有效方式之一[5 ] . ...
Comparison of two new intelligent wind speed forecasting approaches based on wavelet packet decomposition,complete ensemble empirical mode decomposition with adaptive noise and artificial neural networks
1
2018
... 随着能源需求的增加,清洁且丰富的风能得到广泛关注[1 ] .但是风具有间歇性和变异性,导致风电呈现出不稳定性[2 ] .风电的不稳定性给风能管理和电力系统稳定运行提出了巨大挑战,这是造成风电并网困难、利用率低的主要原因之一[3 ] .风电规划和风电预测预报能有效减小这一问题影响[4 ] ,准确的风速预报是提高风电利用率的最有效方式之一[5 ] . ...
A novel forecasting model based on a hybrid processing strategy and an optimized local linear fuzzy neural network to make wind power forecasting:a case study of wind farms in China
1
2017
... 随着能源需求的增加,清洁且丰富的风能得到广泛关注[1 ] .但是风具有间歇性和变异性,导致风电呈现出不稳定性[2 ] .风电的不稳定性给风能管理和电力系统稳定运行提出了巨大挑战,这是造成风电并网困难、利用率低的主要原因之一[3 ] .风电规划和风电预测预报能有效减小这一问题影响[4 ] ,准确的风速预报是提高风电利用率的最有效方式之一[5 ] . ...
Correction and downscaling of NWP wind speed forecasts
1
2007
... 国内外学者提出了多种模型进行风速预测预报,主要分为物理模型和统计模型.物理模型基于物质、能量平衡和空气动力学机理,考虑温度、气压、地形等物理参数进行大空间、长时间风速预测,代表方法有数值天气预报等[6 ] .但物理过程复杂,物理模型所需参数多,且需要长期稳定的气象资料作为驱动数据[7 ] ,不适用于风电场所需要的短期小区域风速预报[8 ] .统计模型主要使用历史风速,通过建立数据间的映射关系实现风速预报.统计模型原理简单,计算量小,适应范围广,具有强大的非线性映射、泛化和自我学习能力.统计模型包括自回归时间序列模型,支持向量机、人工神经网络、极限学习机、卷积神经网络、长短时记忆网络等机器及深度学习模型.这些方法已经被应用于风速预报[9 -14 ] . ...
基于混沌时间序列的支持向量机短期风速预测模型研究
1
2015
... 国内外学者提出了多种模型进行风速预测预报,主要分为物理模型和统计模型.物理模型基于物质、能量平衡和空气动力学机理,考虑温度、气压、地形等物理参数进行大空间、长时间风速预测,代表方法有数值天气预报等[6 ] .但物理过程复杂,物理模型所需参数多,且需要长期稳定的气象资料作为驱动数据[7 ] ,不适用于风电场所需要的短期小区域风速预报[8 ] .统计模型主要使用历史风速,通过建立数据间的映射关系实现风速预报.统计模型原理简单,计算量小,适应范围广,具有强大的非线性映射、泛化和自我学习能力.统计模型包括自回归时间序列模型,支持向量机、人工神经网络、极限学习机、卷积神经网络、长短时记忆网络等机器及深度学习模型.这些方法已经被应用于风速预报[9 -14 ] . ...
基于NARX及混沌支持向量机的短期风速预测
1
2019
... 国内外学者提出了多种模型进行风速预测预报,主要分为物理模型和统计模型.物理模型基于物质、能量平衡和空气动力学机理,考虑温度、气压、地形等物理参数进行大空间、长时间风速预测,代表方法有数值天气预报等[6 ] .但物理过程复杂,物理模型所需参数多,且需要长期稳定的气象资料作为驱动数据[7 ] ,不适用于风电场所需要的短期小区域风速预报[8 ] .统计模型主要使用历史风速,通过建立数据间的映射关系实现风速预报.统计模型原理简单,计算量小,适应范围广,具有强大的非线性映射、泛化和自我学习能力.统计模型包括自回归时间序列模型,支持向量机、人工神经网络、极限学习机、卷积神经网络、长短时记忆网络等机器及深度学习模型.这些方法已经被应用于风速预报[9 -14 ] . ...
基于高斯过程回归和粒子滤波的短期风速预测
2
2020
... 国内外学者提出了多种模型进行风速预测预报,主要分为物理模型和统计模型.物理模型基于物质、能量平衡和空气动力学机理,考虑温度、气压、地形等物理参数进行大空间、长时间风速预测,代表方法有数值天气预报等[6 ] .但物理过程复杂,物理模型所需参数多,且需要长期稳定的气象资料作为驱动数据[7 ] ,不适用于风电场所需要的短期小区域风速预报[8 ] .统计模型主要使用历史风速,通过建立数据间的映射关系实现风速预报.统计模型原理简单,计算量小,适应范围广,具有强大的非线性映射、泛化和自我学习能力.统计模型包括自回归时间序列模型,支持向量机、人工神经网络、极限学习机、卷积神经网络、长短时记忆网络等机器及深度学习模型.这些方法已经被应用于风速预报[9 -14 ] . ...
... 本研究中,小波包分解和卷积长短时记忆网络以及卷积门控循环单元的耦合模型在不同数据集上都表现较好.对于戈壁下垫面,WPD-ELM模型MAPE值为1.33%,WPD-CLSTM模型MAPE值为1.40%,WPD-CGRU模型MAPE值为1.39%.相较于文献[2 ](5.638%)和文献[9 ](8.92%),本研究中模型MAPE值较小,模型预报精度更好.其余下垫面预报结果相似.这表明本研究采用的小波包分解与深度学习模型的耦合模型对风速有较好的预报能力. ...
基于HP-EMD和ARMA的短期风速预测
0
2016
基于EEMD与极限学习机的短期风速组合预测模型
0
2018
基于卷积神经网络和简单循环单元集成模型的风电场内多风机风速预测
0
2020
Data mining-assisted short-term wind speed forecasting by wavelet packet decomposition and elman neural network
0
2018
One dimensional convolutional neural network architectures for wind prediction
1
2019
... 国内外学者提出了多种模型进行风速预测预报,主要分为物理模型和统计模型.物理模型基于物质、能量平衡和空气动力学机理,考虑温度、气压、地形等物理参数进行大空间、长时间风速预测,代表方法有数值天气预报等[6 ] .但物理过程复杂,物理模型所需参数多,且需要长期稳定的气象资料作为驱动数据[7 ] ,不适用于风电场所需要的短期小区域风速预报[8 ] .统计模型主要使用历史风速,通过建立数据间的映射关系实现风速预报.统计模型原理简单,计算量小,适应范围广,具有强大的非线性映射、泛化和自我学习能力.统计模型包括自回归时间序列模型,支持向量机、人工神经网络、极限学习机、卷积神经网络、长短时记忆网络等机器及深度学习模型.这些方法已经被应用于风速预报[9 -14 ] . ...
Four wind speed multi-step forecasting models using extreme learning machines and signal decomposing algorithms
1
2015
... 但单独使用上述模型时预报精度并不理想,需要结合信号分解方法形成混合模型以提高预报精度[15 ] .信号分解方法包括小波分解(Wavelet Decomposition,WD)、小波包分解(Wavelet Packet Decomposition,WPD)、经验模式分解(Empirical Mode Decomposition,EMD)及其改进方法等[16 ] .小波分解可将复杂的原始信号分解为高频信号和低频信号,但该方法仅对信号低频部分详细分解,忽略了信号的高频部分,所以小波分解不适用于包含大量高频信息的信号(如风速)[17 ] ;经验模式分解及其改进方法虽然计算简单,但数学解释不明确[18 ] ,且有残余子信号(噪声);小波包分解数学解释明确,能够自行设定分解层数和分解使用的小波函数,已被广泛应用在风速预报中[19 -21 ] . ...
A novel two-stage forecasting model based on error factor and ensemble method for multi-step wind power forecasting
1
2019
... 但单独使用上述模型时预报精度并不理想,需要结合信号分解方法形成混合模型以提高预报精度[15 ] .信号分解方法包括小波分解(Wavelet Decomposition,WD)、小波包分解(Wavelet Packet Decomposition,WPD)、经验模式分解(Empirical Mode Decomposition,EMD)及其改进方法等[16 ] .小波分解可将复杂的原始信号分解为高频信号和低频信号,但该方法仅对信号低频部分详细分解,忽略了信号的高频部分,所以小波分解不适用于包含大量高频信息的信号(如风速)[17 ] ;经验模式分解及其改进方法虽然计算简单,但数学解释不明确[18 ] ,且有残余子信号(噪声);小波包分解数学解释明确,能够自行设定分解层数和分解使用的小波函数,已被广泛应用在风速预报中[19 -21 ] . ...
Wind speed forecasting approach using secondary decomposition algorithmn and elman neural networks
1
2015
... 但单独使用上述模型时预报精度并不理想,需要结合信号分解方法形成混合模型以提高预报精度[15 ] .信号分解方法包括小波分解(Wavelet Decomposition,WD)、小波包分解(Wavelet Packet Decomposition,WPD)、经验模式分解(Empirical Mode Decomposition,EMD)及其改进方法等[16 ] .小波分解可将复杂的原始信号分解为高频信号和低频信号,但该方法仅对信号低频部分详细分解,忽略了信号的高频部分,所以小波分解不适用于包含大量高频信息的信号(如风速)[17 ] ;经验模式分解及其改进方法虽然计算简单,但数学解释不明确[18 ] ,且有残余子信号(噪声);小波包分解数学解释明确,能够自行设定分解层数和分解使用的小波函数,已被广泛应用在风速预报中[19 -21 ] . ...
Wind speed prediction method based on empirical wavelet transform and new cell update long short-term memory network
1
2019
... 但单独使用上述模型时预报精度并不理想,需要结合信号分解方法形成混合模型以提高预报精度[15 ] .信号分解方法包括小波分解(Wavelet Decomposition,WD)、小波包分解(Wavelet Packet Decomposition,WPD)、经验模式分解(Empirical Mode Decomposition,EMD)及其改进方法等[16 ] .小波分解可将复杂的原始信号分解为高频信号和低频信号,但该方法仅对信号低频部分详细分解,忽略了信号的高频部分,所以小波分解不适用于包含大量高频信息的信号(如风速)[17 ] ;经验模式分解及其改进方法虽然计算简单,但数学解释不明确[18 ] ,且有残余子信号(噪声);小波包分解数学解释明确,能够自行设定分解层数和分解使用的小波函数,已被广泛应用在风速预报中[19 -21 ] . ...
基于小波包分解和改进Elman神经网络的风电场风速和风电功率预测
1
2017
... 但单独使用上述模型时预报精度并不理想,需要结合信号分解方法形成混合模型以提高预报精度[15 ] .信号分解方法包括小波分解(Wavelet Decomposition,WD)、小波包分解(Wavelet Packet Decomposition,WPD)、经验模式分解(Empirical Mode Decomposition,EMD)及其改进方法等[16 ] .小波分解可将复杂的原始信号分解为高频信号和低频信号,但该方法仅对信号低频部分详细分解,忽略了信号的高频部分,所以小波分解不适用于包含大量高频信息的信号(如风速)[17 ] ;经验模式分解及其改进方法虽然计算简单,但数学解释不明确[18 ] ,且有残余子信号(噪声);小波包分解数学解释明确,能够自行设定分解层数和分解使用的小波函数,已被广泛应用在风速预报中[19 -21 ] . ...
基于小波包分解的BP神经网络的短期风速预测
0
2019
Wind speed forecasting method using wavelet,extreme learning machine and outlier correction algorithm
1
2017
... 但单独使用上述模型时预报精度并不理想,需要结合信号分解方法形成混合模型以提高预报精度[15 ] .信号分解方法包括小波分解(Wavelet Decomposition,WD)、小波包分解(Wavelet Packet Decomposition,WPD)、经验模式分解(Empirical Mode Decomposition,EMD)及其改进方法等[16 ] .小波分解可将复杂的原始信号分解为高频信号和低频信号,但该方法仅对信号低频部分详细分解,忽略了信号的高频部分,所以小波分解不适用于包含大量高频信息的信号(如风速)[17 ] ;经验模式分解及其改进方法虽然计算简单,但数学解释不明确[18 ] ,且有残余子信号(噪声);小波包分解数学解释明确,能够自行设定分解层数和分解使用的小波函数,已被广泛应用在风速预报中[19 -21 ] . ...
A new hybrid ensemble deep reinforcement learning model for wind speed short term forecasting
1
2020
... 目前,大量研究通过改进已有模型[1 ] 、应用新方法[22 ] 以及耦合不同信号分解方法[23 ] 等来提高模型预报精度.随着深度学习方法快速发展,在混合模型中加入深度学习模型进行风速预报的研究日益增多.但这些模型预报机理差异大,多种单一模型或与信号分解方法耦合形成的混合模型之间的差异性对比研究不足. ...
Multi-step wind speed forecasting based on hybrid multi-stage decomposition model and long short-term memory neural network
1
2020
... 目前,大量研究通过改进已有模型[1 ] 、应用新方法[22 ] 以及耦合不同信号分解方法[23 ] 等来提高模型预报精度.随着深度学习方法快速发展,在混合模型中加入深度学习模型进行风速预报的研究日益增多.但这些模型预报机理差异大,多种单一模型或与信号分解方法耦合形成的混合模型之间的差异性对比研究不足. ...
Wind speed prediction model using singular spectrum analysis,empirical mode decomposition and convolutional support vector machine
3
2019
... 支持向量回归属于支持向量机,主要应用于回归问题.其核心思想是寻找一条最佳拟合曲线,在容忍偏差范围内,曲线包含尽可能多的数据点.回归方程的数学描述为[24 ] : ...
... 支持向量回归的优化问题描述为[24 ] : ...
... 支持向量回归的预报可以定义为[24 ] : ...
A data-driven multi-model methodology with deep feature selection for short-term wind forecasting
3
2017
... 梯度提升回归是一种集成学习算法[25 ] ,该算法基于分类回归树(Classification and regression tree, CART)和序列提升算法构建.算法目的是最小化损失函数,减小残差.为实现此目的,首先计算初始模型残差,在梯度下降方向使用残差拟合基础学习器,再使用拟合后的基础学习器更新模型,不断重复上述过程获得目标模型. ...
... 人工神经网络受人类大脑结构启发得到,由一系列相互连接的神经元构成.网络内部不同神经元之间通过权重相连,神经元内设有激活函数和偏差.根据激活函数和学习算法的不同,人工神经网络可以分为不同类别.其数学描述为[25 ] : ...
... (3) 不同模型具有不同学习能力,本研究中主要体现在极值预报上.在极值点处单一模型预报误差较大,而多模型平均使得预报结果更加平滑,预报值更接近实际观测值.多模型平均能有效利用不同模型特点,在极值预报上实现互补.Feng等[25 ] 使用深度特征选择和多模型预报风速,模型预报精度明显优于单一模型. ...
An experimental investigation of three new hybrid wind speed forecasting models using multi-decomposing strategy and ELM algorithm
1
2018
... 极限学习机是一类包含单个隐藏层的前馈神经网络[26 ] ,该算法的最大特点是保证学习精度的前提下训练速度更快.极限学习机在训练模型前,首先随机初始化输入权重和偏差,同时确定输出矩阵.不同于传统神经网络,极限学习机在迭代时不需要更新全部参数,仅通过输出矩阵求解相应方程组就能快速训练模型.其损失函数描述为[27 ] : ...
Smart multi-step deep learning model for wind speed forecasting based on variational mode decomposition,singular spectrum analysis,LSTM network and ELM
1
2018
... 极限学习机是一类包含单个隐藏层的前馈神经网络[26 ] ,该算法的最大特点是保证学习精度的前提下训练速度更快.极限学习机在训练模型前,首先随机初始化输入权重和偏差,同时确定输出矩阵.不同于传统神经网络,极限学习机在迭代时不需要更新全部参数,仅通过输出矩阵求解相应方程组就能快速训练模型.其损失函数描述为[27 ] : ...
Smart deep learning based wind speed prediction model using wavelet packet decomposition,convolutional neural network and convolutional long short term memory network
4
2018
... 卷积神经网络能够提取数据特征,在处理时间序列数据方面有良好表现.相较于支持向量机和人工神经网络等浅层模型,卷积神经网络模型特有的卷积层可以实现自动特征选取,其全连接层处理有短期依赖的高频子集能力强[28 ] .卷积层内,各个神经元间无相互联系,只共享卷积核权重.相较于人工神经网络,该模型训练更有效.每个卷积层的数学描述为[29 ] : ...
... 循环神经网络是一种处理时间序列数据的方法,但传统循环神经网络训练过程中常出现梯度消失或梯度爆炸问题.为解决此问题,提出了长短时记忆网络[30 ] ,该方法能有效处理长短期依赖问题.长短时记忆网络的核心组件为输入门、遗忘门和输出门.输入门决定细胞状态中存储的信息,遗忘门决定被遗忘的信息,输出门决定最终输出.单个神经元计算过程为:①输入数据,输入门激活,计算输入细胞信息;②如果遗忘门激活,遗忘部分细胞中保留的历史状态;③输出门激活,计算输出信息.神经元内计算过程可以描述为[28 ] : ...
... 式中:x =(x 1 , x 2 , x 3 ,…,xT )为展开层数据;it 为输入门;ft 为遗忘门;ct 为记忆细胞的激活矢量;ot 为输出门;mt 为每个记忆块的激活矢量;w 为权重矩阵;b 为偏差矢量;°为点积;σ 和tanh 为激活函数,激活函数数学描述为[28 ] : ...
... 根据已有文献,常用混合模型大多为信号分解方法和基础预报模型组成.由于信号分解子集各有特点,一些混合模型仅使用一种基础预报模型预报所有子集[30 ] ,另一些模型针对不同频率子集使用不同模型进行预报[28 ] .本实验方案为:①选择应用广泛的机器学习和最新的深度学习模型共12个作为基础预报模型(简称单一XXX模型,表1 ),研究各种单一模型在风速预报中的表现;②小波包分解与12个基础预报模型耦合(简称WPD-XXX混合模型),探索小波包分解在提高模型预报精度中的作用;③小波包分解与12个基础预报模型和卷积神经网络(CNN)耦合(简称WPD-XXX-CNN混合模型),这里CNN用于预报小波包分解子集中的高频子集,而12个单一XXX模型用于预报低频子集.单一XXX模型作为对照组,WPD-XXX混合模型和WPD-XXX-CNN混合模型为实验组.单一XXX模型对照组中,使用12个基础预报模型直接预报风速;WPD-XXX实验组中,先将风速分解为低频和高频子集,再由XXX模型分别预报所有子集,最后将子集预报结果相加得出最终预报结果;WPD-XXX-CNN实验组中,利用卷积神经网络模型预报高频子集,XXX模型预报低频子集,最后将子集预报结果相加,得到最终结果.算法流程见图1 . ...
A deep hybrid learning model to detect unsafe behavior:integrating convolution neural networks and long short-term memory
1
2018
... 卷积神经网络能够提取数据特征,在处理时间序列数据方面有良好表现.相较于支持向量机和人工神经网络等浅层模型,卷积神经网络模型特有的卷积层可以实现自动特征选取,其全连接层处理有短期依赖的高频子集能力强[28 ] .卷积层内,各个神经元间无相互联系,只共享卷积核权重.相较于人工神经网络,该模型训练更有效.每个卷积层的数学描述为[29 ] : ...
A new short-term wind speed forecasting method based on fine-tuned LSTM neural network and optimal input sets
2
2020
... 循环神经网络是一种处理时间序列数据的方法,但传统循环神经网络训练过程中常出现梯度消失或梯度爆炸问题.为解决此问题,提出了长短时记忆网络[30 ] ,该方法能有效处理长短期依赖问题.长短时记忆网络的核心组件为输入门、遗忘门和输出门.输入门决定细胞状态中存储的信息,遗忘门决定被遗忘的信息,输出门决定最终输出.单个神经元计算过程为:①输入数据,输入门激活,计算输入细胞信息;②如果遗忘门激活,遗忘部分细胞中保留的历史状态;③输出门激活,计算输出信息.神经元内计算过程可以描述为[28 ] : ...
... 根据已有文献,常用混合模型大多为信号分解方法和基础预报模型组成.由于信号分解子集各有特点,一些混合模型仅使用一种基础预报模型预报所有子集[30 ] ,另一些模型针对不同频率子集使用不同模型进行预报[28 ] .本实验方案为:①选择应用广泛的机器学习和最新的深度学习模型共12个作为基础预报模型(简称单一XXX模型,表1 ),研究各种单一模型在风速预报中的表现;②小波包分解与12个基础预报模型耦合(简称WPD-XXX混合模型),探索小波包分解在提高模型预报精度中的作用;③小波包分解与12个基础预报模型和卷积神经网络(CNN)耦合(简称WPD-XXX-CNN混合模型),这里CNN用于预报小波包分解子集中的高频子集,而12个单一XXX模型用于预报低频子集.单一XXX模型作为对照组,WPD-XXX混合模型和WPD-XXX-CNN混合模型为实验组.单一XXX模型对照组中,使用12个基础预报模型直接预报风速;WPD-XXX实验组中,先将风速分解为低频和高频子集,再由XXX模型分别预报所有子集,最后将子集预报结果相加得出最终预报结果;WPD-XXX-CNN实验组中,利用卷积神经网络模型预报高频子集,XXX模型预报低频子集,最后将子集预报结果相加,得到最终结果.算法流程见图1 . ...
Smart wind speed forecasting approach using various boosting algorithms,big multi-step forecasting strategy
1
2019
... 小波包分解源于小波分解,它在分解信号低频子集同时,对高频子集继续分解.因此,该方法适用于分解含有大量高频信息的风速信号,以获取更加准确的信息.小波包分解使用时仅需要设置小波函数和分解层数.根据分解的信号类别,小波包分解可分为离散小波转换和连续小波转换.由于风速的连续性,本研究使用连续小波转换,数学描述为[31 ] : ...
Short-term wind speed prediction model based on GA-ANN improved by VMD
1
2020
... 基于现有研究的数据组织方式[32 ] ,本研究风速数据重构过程如图3 .选择6个历史数据作为输入数据,数据重构时,每次选取7个数据为一组样本,平移1个位置选取下一组样本.因此,前后两组样本数据中有6个相同数据.最终得到694组样本数据,并以594∶100的比例划分为训练集和测试集.数据重构前进行最大最小值标准化,公式为: ...
An adaptive hybrid model for short term wind speed forecasting
2
2019
... 为了对比分析模型预报精度,本研究使用3种精度指标:平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)、平均绝对误差(Mean Absolute Error, MAE)和均方根误差(Root Mean Square Error, RMSE)[33 ] . ...
... (1) 信号分解能有效降低数据复杂性,机器学习模型对分解后的风速信号预报能力更强.原始风速具有间歇性和不稳定性,信号复杂,机器学习模型对其预报能力差.但信号分解方法可将复杂的原始信号转换为更加稳定的分量,降低了原始风速内在特性的影响,机器学习模型对各稳定分量的预报精度更高,因此,单一XXX模型与小波包分解组成的混合模型对风速的预报能力大大增强.这与Zhang等[33 ] 的研究结果一致. ...
A novel two-stage forecasting model based on error factor and ensemble method for multi-step wind power forecasting
1
2019
... (2) 深度学习模型对复杂时间序列预报能力更强.卷积长短时记忆网络和卷积门控循环单元既具有卷积神经网络的自动特征选择功能,又具有循环神经网络的记忆功能.ELM为单个隐藏层前馈神经网络,模型结构简单,训练速度快,不需要复杂的参数选择就能快速学习数据的内部规律.Hao等[34 ] 使用极限学习机预报风速分量以及风速误差序列,Ghimire等[35 ] 在深度太阳辐射预报中使用卷积长短时记忆网络,Liu等[36 ] 使用卷积门控循环单元预报风速序列子集,都有着相似发现. ...
Deep solar radiation forecasting with convolutional neural network and long short-term memory network algorithms
1
2019
... (2) 深度学习模型对复杂时间序列预报能力更强.卷积长短时记忆网络和卷积门控循环单元既具有卷积神经网络的自动特征选择功能,又具有循环神经网络的记忆功能.ELM为单个隐藏层前馈神经网络,模型结构简单,训练速度快,不需要复杂的参数选择就能快速学习数据的内部规律.Hao等[34 ] 使用极限学习机预报风速分量以及风速误差序列,Ghimire等[35 ] 在深度太阳辐射预报中使用卷积长短时记忆网络,Liu等[36 ] 使用卷积门控循环单元预报风速序列子集,都有着相似发现. ...
Smart wind speed deep learning based multi-step forecasting model using singular spectrum analysis,convolutional gated recurrent unit network and support vector regression
1
2019
... (2) 深度学习模型对复杂时间序列预报能力更强.卷积长短时记忆网络和卷积门控循环单元既具有卷积神经网络的自动特征选择功能,又具有循环神经网络的记忆功能.ELM为单个隐藏层前馈神经网络,模型结构简单,训练速度快,不需要复杂的参数选择就能快速学习数据的内部规律.Hao等[34 ] 使用极限学习机预报风速分量以及风速误差序列,Ghimire等[35 ] 在深度太阳辐射预报中使用卷积长短时记忆网络,Liu等[36 ] 使用卷积门控循环单元预报风速序列子集,都有着相似发现. ...




 甘公网安备 62010202000688号
甘公网安备 62010202000688号